重视概念生成，关注方法归纳——听公开课《反比例函数》后的思考

福建永安六中 张菊英

《数学课程标准》提出的：“人人学有价值的数学”“人人都能获得必须的数学”“不同的人在数学上获得不同的发展!”如何能在课堂上实现这三个目标呢?尤其是在概念课的教学中，我们往往会陷入困惑：怎样让学生理解抽象的数学概念?用什么方法引导学生应用数学概念解决问题?一直以来，都是我们全组数学教师思考并努力想解决的问题。2017年，地区数学学科教学研讨会在我校召开，罗老师上示范课，上了《反比例函数》(北师大版第六章第一节)这节课，听完课让我对概念课教学又多了一些认识：学生的数学学习应当是现实的有意义的富有挑战性的；有效的数学学习活动不能单纯地依赖模仿与记忆；数学教学活动应重视概念生成，关注方法归纳。

案例：《反比例函数》(北师大版第六章第一节)教学案

一、课前准备、引入新课

1.请同学们观察下列图象，它们是否反映y是x的函数？你是怎么理解函数概念的？

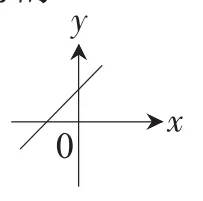
图1

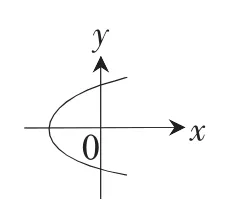
图2

2.李大爷要围成一个矩形养鸡场，养鸡场的一边利用足够长的墙，用篱笆围成的另外三边总长恰好为24米，要围的养鸡场是如图所示的矩形ABCD，设BC的边长为x米，AB边的长为y米，则y与x之间的关系式是_________；y是x的函数吗？

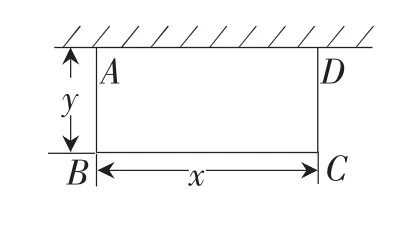
《数学课程标准》提出的:数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。罗老师以旧带新设计的题目，有利于学生主动地进入本节课的学习。

变式：篱笆足够多，要使围成的矩形养鸡场面积始终是24m2，则y与x之间的关系式是___________；y是x的函数吗？

罗老师及时对题目进行变式，利用学生认知结构中的有关知识，提供产生数学问题的背景，为新课的学习指明方向。

二、识记目标、明确要求

1.领会反比例函数的意义，理解并掌握反比例函数的概念。

2.会判断一个函数是不是反比例函数。

3.能根据实际问题中的条件确定反比例函数的关系式。

学生齐读本节课的学习目标，开门见山地告诉学生：本节课要学习的数学内容；提纲挈领，明确本节课知识的重难点。

三、整合知识、指导方法

1.每位同学都思考一个类似于矩形养鸡场中变量x，y的变化关系的实际例子，并写出两个变量之间的关系式，用列表法说明两个变量之间是否存在函数关系。

2.小组交流实例，派代表展示。

3.分析所建立的函数模型的共同特征。

4.抽象概括：一般地，如果两个变量x，y之间对应的关系可以表示成k为常数，且k≠0）的形式，那么称y是x的函数.自变量x不能为零。

《数学课程标准》提出：数学学习内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动。内容的呈现应采用不同的表达方式，以满足多样化的学习需求。罗老师以实际问题作为载体，开展小组合作活动,激发了学生的学习积极性，为学生提供交流和展示的平台。很好地体现了：有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式的教学理念，使得反比例函数概念的生成变得水到渠成。

四、合作探究、展示交流

1.某村有耕地246.2hm2，人口数量n逐年发生变化，那么该村人均占有耕地面积m（hm2/人）是全村人口数n的函数吗？是反比例函数吗？

3.关系式xy+4=0中y是x的反比例函数吗?若是，相应的k值等于多少？若不是，请说明理由。

5.下列函数表达式中，x均表示自变量，那么哪些是反比例函数？相应的k值是多少？

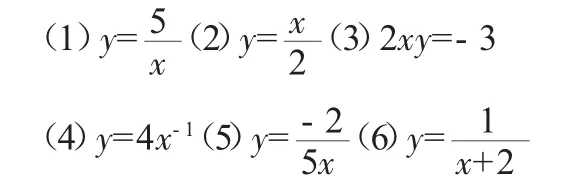
6.已知：y是x的反比例函数，且当x=2时，y=-3，求当x=-3时y的值。

数学概念来源于生活，也要在生活中得到运用。让学生用学到的数学概念解决日常生活中的实际问题，是概念教学中培养学生思维能力的有效手段。罗老师在题目的选择上作了精心的布置：第一题是实际问题，直接对概念进行再认识；第二题是对概念的充要条件的理解；接着安排题目有针对性的进行训练，利用题目帮助学生理解概念。

五、当堂巩固、内化提升

1.下列函数中，为反比例函数的是（）.

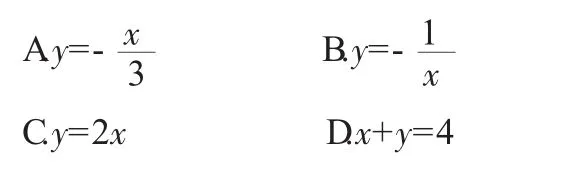
2.当路程s一定时，速度v与时间t之间的函数关系是（ ）.

A.正比例函数 B.一次函数

C.反比例函数 D.以上均不正确

3.若函数 y=（a-2）xa2-5是关于 x 的反比例函数，则a=______。

4.已知y是x的反比例函数，下面表格给出了x与y的一些值，则a=_____；b=______；c=______。

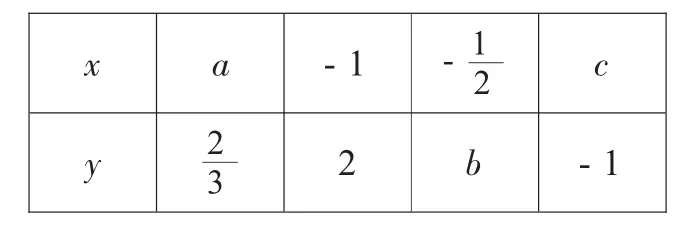
由于数学概念的抽象性,学生在概念学习过程中往往不容易抓住概念的本质属性,罗老师结合概念本身特点及学生认知水平恰当地编制一些习题,使学生在理解概念的基础上更好的应用概念，教学中不忘引导学生归纳解题的方法。

5.小结反思:本节课有何收获和体会？

让学生畅所欲言,发表自己的看法,从而更好地了解学生的学习情况,罗老师适当补充,将反比例函数的概念具体化。

六、布置作业、课后思考

《优化设计》反比例函数第1课时

案例分析与思考：

数学概念是反映一类事物在数量关系和空间形式方面的本质属性的思维形式，是导出数学定理、公式、法则、性质的出发点，是学生建构认知结构的着眼点。所以，概念教学是教师帮助学生打好数学基础的关键，是帮助学生更好地理解数学的必经之路.数学概念来源于生活，也要在生活中得到运用。让学生用学到的数学概念解决日常生活中的实际问题，是概念教学中培养学生思维能力的有效手段。

罗老师在课堂上始终关注学生的学习动向，始终关注学生的心理活动，始终关注学生的情感变化，让学生真正成为课堂的主人，给学生创设一种和谐的学习氛围，引导学生学会倾听,学会交流,学会展示；教学过程的整体设计体现了:重视概念生成,关注方法归纳。

1.重视概念生成。

抽象概念的教学要关注概念的实际背景与形成过程，帮助学生克服机械记忆概念的学习方式。以情境作为教学工具，引导学生从特殊过渡到一般，不但能激发学生学习兴趣，同时还兼具设疑释疑的功能。我们知道，数学概念具有：(1)反映一类对象在数与形方面内在的，固有的属性；(2)是人类对现实世界的空间形式和数量关系的简明概括的反映，并且都由反映概念本质特征的符号来表示。这两个特点。罗老师在课前引入部分：设计两道题，一是再现函数的概念，结合图形理解函数定义减轻学生的记忆负担；二是用实际问题引导学生关注生活中存在量的变化，体验量的变化又有密切的相互依赖。在复习旧知的前提下，对原题进行变式，列出新的表达式，引出新函数。符合学生的心理发展规律；符合概念生成的渐进性原则。教学以”五步教学法”进行，每个环节都为了让学生感受函数概念的生成。

2.关注方法归纳。

抽象概念的教学其目的是让学生能在理解概念的基础上，能应用概念解决问题，也就是能在解题过程中，关注解题方法的归纳。罗老师在第二环节设计小组活动,让学生进行充分的自主活动，学生不仅有机会经历概念产生的过程，还能了解概念的条件，把握概念形成的规律，学生在小组合作交流中与小组成员共同实践、思考、探索、归纳新知识、找到新方法。例题与习题的编制，逐层深入地引导学生理解概念、寻找解决问题的最佳途径。这样的教学思路。有利于学生关注利用函数概念解决问题的方法。