突扩式消力池T型水跃的流速分布与边界层发展

傅铭焕，侯 毅，陈炳斌，潘龙泉，张志昌，陈 昊

(1.浙江省水利水电勘测设计院，浙江 杭州 310002；2.浙江铭诚建设有限公司， 浙江 绍兴 312030；3.西安理工大学，陕西 西安 710048)

突扩式水跃是指下泄急流突然扩散到下游较宽渠道，在下游渠道中过渡为缓流的一种三元空间水跃.根据下游渠道尾水水深的不同，可将突扩式水跃分为R型水跃、S型水跃和T型水跃[1].当下游渠道尾水水深较浅，水跃跃前断面位于扩散后的下游渠道中，此时水跃称为R型水跃.当下游水深较大，跃前断面位于上游较窄渠道而跃后断面位于下游较宽渠道，此时称为T型水跃.当跃前断面位于突然扩散断面附近，此时发生的水跃称为S型水跃.

文献[1]通过模型试验，研究了S型淹没水跃水跃区沿程断面流速分布、水跃跃后水深、水跃长度及消能率的变化规律.文献[2]试验研究了突扩式水跃的水力特性，提出了S型水跃和R型水跃跃后水深、横向水面线、壁面切应力系数、水跃长度、断面最大流速分布和边界层厚度的变化规律.卢士强[3]试验研究了S型突扩式水跃的水力特性，给出了突扩式水跃跃后水深计算的经验公式.汪涛,等[4]假定跃首断面到跃尾断面的水面线符合抛物线分布，提出了S型水跃跃后水深的计算方法.Μ·Д.切尔托乌索夫[5]亦利用动量方程，假定边界压力符合静压分布，研究了跌扩型-突扩消力池共轭水深的计算方法，并对其进行了验证.傅铭焕,等[6]通过绕流阻力理论，结合水跃区动量方程公式求解S型水跃跃后水深并获得了较好的计算效果.文献[7]建立水跃区水体质点的运动方程，研究了S型水跃跃长的变化规律，并给出了突扩式水跃跃长的计算公式.

文献[8]试验研究了T型水跃，水跃区断面流速分布、最大流速沿程分布和边界层的沿程变化规律，但并未给出断面流速、最大流速及边界层的计算公式.

作为三元空间水跃，突扩式水跃的水力特性较一般二元水跃更加复杂.由以上研究可以看出，突扩式水跃远没有一般二元水跃研究的深入和透彻.作者旨在根据文献[8]的流速分布规律，研究T型突扩式水跃断面流速分布和最大流速沿程分布的计算方法，为T型水跃宏观研究(跃后水深、水跃长度、消能率等)提供计算基础与参考.

1 断面流速分布及最大流速沿程分布

文献[8]试验研究了突扩比等于2时的T型突扩式水跃的水力特性，模型试验的流量Q=1.45-5.24 L/s，跃前断面水深h1=0.01-0.018 m，跃前断面平均流速v1=0.96-2.19 m/s，跃前断面弗劳德数Fr1=3.54-6.39，雷诺数R1=8 754-43 729，试验模型(见图1).图中，b1为上游渠道宽度，B为下游渠道宽度，h2为跃后断面水深，v2为跃后断面平均流速，Lr为水跃旋滚长度.文献[8]实测的各断面流速(见图2)，图中x轴表示水流主流流向；y轴表示垂直于水流方向(竖向)；Um为水跃区各断面最大流速；u为水跃区水流各质点流速；b为垂直水流方向上水质点流速等于该断面最大流速一半时(∂u/∂y<0)，该水质点距离床面的垂直距离.

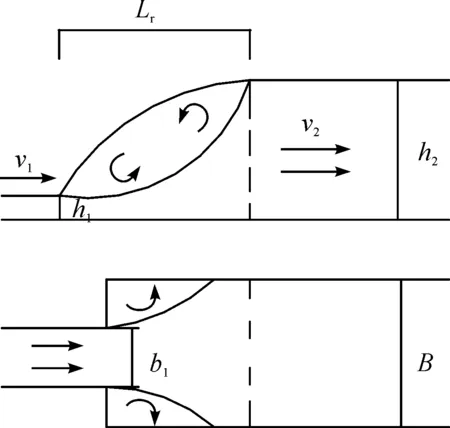
图1 T型突扩式水跃示意图

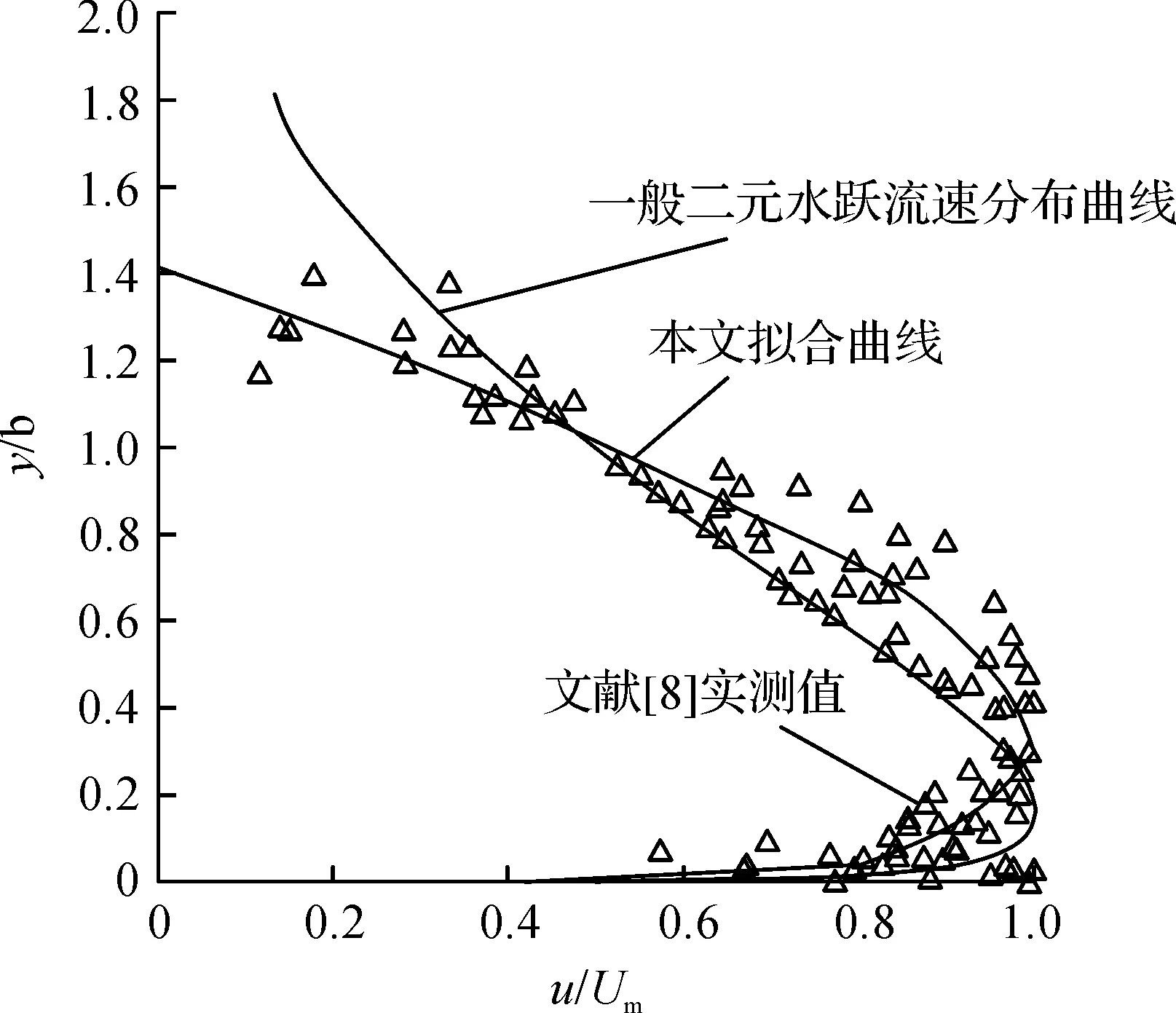
图2 断面流速分布

从图2可以看出，T型突扩式水跃，水跃区断面流速分布具有相似性，水跃区沿程各断面流速具有同一分布规律.断面流速从床面底部开始沿垂直水流方向逐渐增大到最大流速，之后沿垂直水流方向又开始逐渐减小.床面底部距最大流速处的垂直距离即为边界层厚度δ，这一区域称为边界层区.在边界层上部，断面流速逐渐衰减，这一区域称为混合区.由上可知，T型突扩式水跃断面流速分布规律与一般二元水跃断面流速分布规律一致.但T型突扩式水跃边界层厚度为0.3b，而一般二元水跃的边界层厚度仅为0.16b.

由图2可知，T型水跃断面流速分布较为复杂，用同一流速公式来描述较为困难.笔者根据文献[8]的试验数据，对边界层区域和混合区断面流速分别进行分析，发现T型突扩式水跃边界层内流速分布可表示为

u/Um=1.140 5(y/b)0.109 5

(1)

将边界层厚度δ=0.3b代入公式(1)可得，

u/Um=(y/δ)0.109 5

(2)

由公式(2)可知，T型水跃边界层内流速分布同一般二元水跃边界层流速分布相似，都符合指数律分布.一般二元水跃指数n=0.071 4-0.166 7[9-10]，而T型水跃在雷诺数R1=875 4-437 29时，其指数n=0.109 5.

笔者对边界层流速分布进行进一步分析，发现流速分布也可用对数律表示，即

(3)

将边界层厚度δ=0.3b代入式(3)可得，

(4)

由式(2)和式(4)可知，边界层内相对流速u/Um随相对距离y/b的增大而增大.

对于混合区流速，其流速分布较为复杂，需用高次方程才能表示，即

(5)

公式(5)可变形为

(6)

文献[8]给出了相对最大流速Um/v1随相对距离x/h1的变化规律(见图3).由图3可以看出，T型水跃水跃区断面最大流速沿水流主流方向逐渐衰减.本文对文献[8]的最大流速进行拟合，得到相对最大流速的沿程分布公式，即:

Um/v1=1.01e-0.056 5(x/h1)

(7)

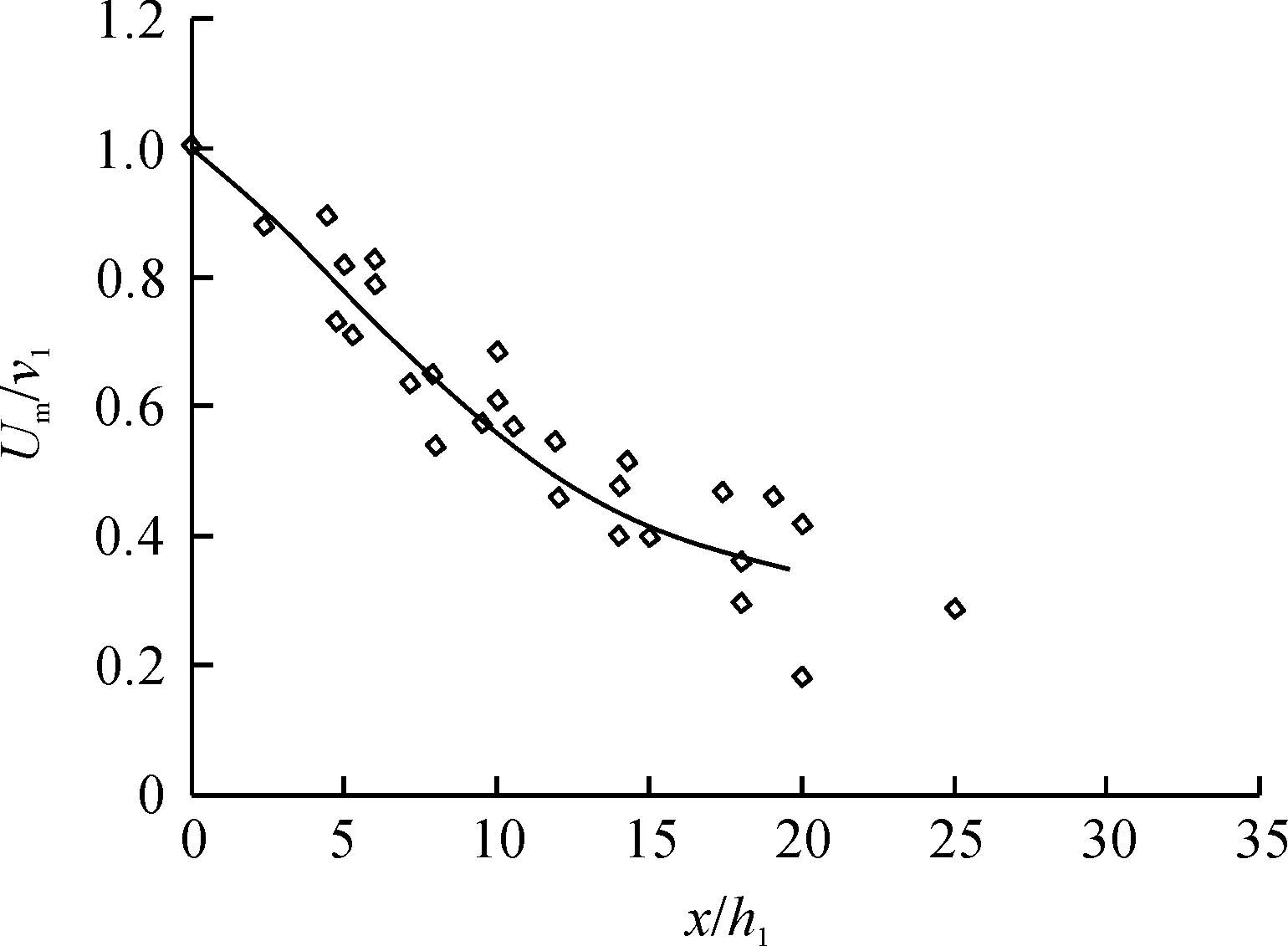
图3 最大流速沿程分布

2 水跃区边界层的发展

边界层的位移损失厚度δ1和动量损失厚度δ2可分别表示为:

(8)

(9)

将公式(2)依次代入式(8)、式(9)，可求解得T型水跃δ1=0.098 7δ，δ2=0.081δ.

紊流边界层内Karman动量积分方程可用下式表示:

(10)

式中：H—形状系数；H=δ1/δ2=1.218 5；

τ0—壁面切应力；ρ—水流的密度.

对于消力池内的水流边界层发展仍可以用Karman的动量积分方程求解，水跃区虽然有水流旋滚，但其主流仍然在底部，是一种贴底的附壁射流.MYERS G. E,等[10]采用Karman的动量积分方程来研究附壁紊动射流的紊流边界层发展.N.RAJARATNAM,等[11-12]认为水跃实质上是一种贴底的附壁射流，可以用附壁射流的理论来研究水跃的水力特性.J.S.MONTES,H[13]在对不完全水跃的研究中，也采用Karman的动量积分方程求解边界层的动量损失厚度.张志昌，等[14-15]利用附壁射流理论研究了水跃区紊流边界层及共轭水深的变化规律.傅铭焕[16]也利用Karman的动量积分方程并结合附壁射流理论研究了粗糙壁面消力池水跃区紊流边界层沿程发展、壁面切应力、水跃跃后水深、水跃旋滚长度等水力特性.可见，用附壁射流理论研究水跃现象越来越普遍，其研究方法亦愈加成熟.

根据SHLICHTING T[17]的研究，平板上的切应力公式为:

(11)

式中：ν—水流运动粘滞系数.

将式(11)代入式(10)，可得:

(12)

上式变形可得:

(13)

式中：H—一般在1.2～1.3范围内变化，故求解公式(13)时可以假定为常数[18].

对于无限平板，Um为沿程不变，即dUm/dx=0.但在水跃区，Um沿程逐渐衰减.令等式(13)右边为零，求解得[14]：

(14)

将式(14)对x求导，得：

(15)

将式(15)代入式(13)化简得：

(16)

将公式(7)代入式(16)可得:

C1/4dC=ξν1/4(1.01v1)(9+5H)/4[e-0.056 5(x/h1)](9+5H)/4dx

(17)

对式(17)进行积分，可得:

C5/4=

(18)

当x=0时，边界层厚度δ=0，边界层动量损失厚度δ2=0.081δ=0，故C=0，可得:

(19)

将式(19)代入公式(18)，可得:

C=

(20)

将式(7)、式(20)代入公式(14)得:

(21)

Sigalla给出的壁面切应力系数公式为[14]:

(22)

由式(11)=式(22)可得ξ=0.015 07.

将H=1.218 5，ξ=0.015 07代入式(21)，则公式(21)简化为：

(23)

将δ2=0.081δ代入公式(23)可得T型水跃边界层厚度δ为:

(24)

由式(24)可知，T型水跃边界层厚度δ沿程逐渐发展，边界层厚度δ是水流运动粘滞系数ν、跃前断面水深h1、跃前断面平均流速v1和沿程距离x的函数.

3 公式验证

文献[8]虽给出了相对边界层厚度δ/b随x/h1的变化规律，但其试验所测的b/h1试验点分布较为分散，b/h1随x/h1变化的经验公式精度较低.笔者对其边界层重新进行分析，结果(见图4).

图4 相对边界层厚度δ/h1随x/h1的变化

由图4可知，相对边界层厚度δ/h1沿程逐渐发展.图4中还绘入了公式(24)的计算值.由图4可知，公式(24)的计算值与文献[8]的实测值整体较为接近；在整个水跃旋滚范围内，公式(24)计算的相对边界层厚度δ/h1的发展速率略微偏大.在2

4 结 语

本文通过实测资料，分析了T型突扩式水跃,水跃区断面流速和最大流速的分布规律，并给出了断面流速和最大流速的计算公式.研究发现，T型水跃边界层内流速分布同一般二元水跃分布相似，即流速分布即服从指数律也服从对数律分布.水跃区相对最大流速沿程逐渐衰减.水跃区边界层厚度逐渐增加，边界层厚度是水流运动粘滞系数、跃前断面水深、跃前断面平均流速和沿程距离的函数.本文给出了水跃区边界层厚度的沿程发展公式，并用实测资料对其进行了验证.

信息启示

法国里尔大学Zaoui Ali教授来校作学术报告

4月12日下午，我校客座教授Zaoui Ali先生在教学科研楼407作了题为“土木工程材料及水环境研究最新进展”的学术报告.报告会由邹冰副校长主持，河海大学管仪庆教授担任现场翻译，水利学院、测市学院负责人及师生代表共60余人参加.

Zaoui Ali先生从2005年2月起担任法国里尔大学科学与技术工程学科的教授，2017年被聘为特殊二级教授(法国最高级别教授).Ali教授研究兴趣广泛，他的主要研究方向包括分子动力学、蒙特卡罗的建模和模拟方法等，他是第一个在纳米级土木工程材料领域进行建模工作的研究人员.

报告会上，Zaoui Ali教授介绍了里尔大学的基本情况，接着，Ali教授与师生分享了他最新的研究成果——粘土和混凝土中加入纳米级复合材料后的性质改变及在土木工程材料、核废料处置、水污染治理领域中的应用.Ali教授还高兴地给大家介绍了他与中国学生合作完成的科研成果.

报告会结束前，师生们就感兴趣的科研问题以及法国留学相关问题和Ali教授进行了热烈的交流，大家感觉受益匪浅.

摘自浙江水利水电学院网