渐扩式消力池水跃长度的分析与计算
2018-05-09张田
张田
(浙江省水利水电勘测设计院,浙江 杭州 310002)
当溢洪道出口较窄而下游河道较宽时,常采用渐扩式消力池,用以衔接上游水流与下游河槽.发生于渐扩式消力池中的水跃称渐扩式水跃.
张志恒[1]通过研究陡坡扩散消力池的水工模型试验发现,渐扩式消力池跃后水深较同一流量下一般矩形二元水跃跃后水深小4%~14%.陈椿庭[2]研究表明,当渐扩式水跃跃后断面宽度与跃前断面宽度比b1/b1=2时,所需的下游水深可减小1/10.可见,渐扩式消力池较一般矩形消力池具有更好的消能效果.
渐扩式水跃的研究主要包括水跃跃后水深与水跃长度.现阶段很多学者提出了渐扩式水跃跃后水深的计算方法[1,3-6],渐扩式水跃跃后水深的研究已比较成熟.而渐扩式水跃长度的研究远没有水跃跃后水深研究的深入和透彻,我国溢洪道设计规范[7]虽给出了渐扩式水跃跃后水深的计算方法,但未给出渐扩式水跃长度的计算公式.作者旨在分析现有渐扩式水跃长度公式的适用性的基础上,提出新的渐扩式水跃长度的计算方法,以供设计参考.
1 现有渐扩式水跃长度公式的分析
现行的水跃长度计算公式主要如下:
中国水利水电科学研究院水跃长度计算公式为:[8]
Lj=9.4h1(Fr1-1)[1-11.915/(m1.5β0.5)]
(1)
式中:Lj为渐扩式水跃长度;h1为跃前断面水深;Fr1为跃前断面弗劳德数;m=1/tanθ,θ为边墙扩散角;β=b1/h1,b1为消力池入口宽度.
Игнзтенко[8]认为Lj=
(2)
Kolseus,H.J.[8]认为Lj=(4±0.5)ηh1
(3)
式中:η=(h2-h1)/h1,跃前水深h1≈0.002~0.005 m.
Khakfa,A.M.[8]认为Lj=3ηh1
(4)
式(4)适用范围为b1/h1=1.3.
吴宇峰[8]认为Lj=
(5)
式(5)适用范围为b1/h1>2,2 (6) (7) 陕西水利科学研究院[10]认为 Lj=0.077h1(Fr1·ctgθ)1.5 (8) 式(8)适用范围为3.5 笔者根据张志恒[1]水工模型试验的上游实测资料(见表1),将各公式计算的渐扩式水跃长度值分别绘入图1. 表1 渐扩式水跃上游实测资料 图1 渐扩式水跃长度的比较 由图1可知,上述公式计算的渐扩式消力池相对水跃长度Lj/h1在跃前断面弗劳德数3.5 由上述分析可知,在跃前断面弗劳德数3.5 由图1可知,渐扩式消力池相对水跃长度随跃前断面弗劳德数近似服从线性分布,根据上文分析结果,笔者在3.5 Lj/h1=7.534 3Fr1-8.106 4 (9) 相对水跃长度随跃前断面弗劳德数的增大而增大. 我国溢洪道设计规范要求设计者在设计扩散水跃跃长时按棱柱体水跃跃长的0.8倍计算,其未考虑边墙扩散角的影响[7].公式(9)计算值虽位于各家公式中间,具有较好的计算效果,但该公式也未考虑渐扩式消力池边墙扩散角θ的影响,公式形式存在一定的缺陷.实际工程中,边墙扩散角θ通常较小,一般要求θ<12°.因为当θ值较大时,扩散段中的水流就有可能扩散不佳,致使边壁处产生回流[4].吴宝琴等[10]的试验结果表明当θ=9°时,水流出现脱壁现象,在边壁处有回流产生.可见,实际工程中边墙扩散角的变化范围较小.同时,傅铭焕等[5]的研究亦表明,渐扩式消力池(扩散角θ<9°)不考虑边墙扩散角影响的局部阻力系数对其水跃跃后水深计算影响不大. 图2 渐扩式水跃长度(θ=3°) 图3 渐扩式水跃长度(θ=8°) 本文借助文献[1]水工模型试验的上游实测资料,改变边墙扩散角来验证公式(9)的结构合理性.边墙扩散角θ=3°和θ=8°两种工况下,公式(1)、公式(2)、公式(5)、公式(6)、公式(7)、公式(8)、公式(9)计算的相对水跃长度分别如图2和图3所示. 由图2和图3可知,公式(8)计算值对边墙扩散角θ的变化最为敏感,在θ=3°工况下,其计算值大于其余公式计算值约120%-174%;而在θ=8°工况下,其计算值小于其余公式计算值约35%-45%.其余6家公式在3.5 从图2和图3可以看出,在边墙扩散角θ=3°工况下,公式(9)计算的相对水跃长度在跃前断面弗劳德数3.5 本文根据实测资料,分析了已有渐扩式消力池水跃长度公式的合理性.分析发现,相对水跃长度随跃前断面弗劳德数的增大而增大,相对水跃长度随跃前断面弗劳德数近似呈线性分布.在3.5 参考文献: [1] 张志恒.矩形扩散水跃的水力计算[J].陕西水利,1973(1):10-26. [2] 陈椿庭,姜国干.水工模型试验[M].2版.北京:水利电力出版社,1985:316-320. [3] 吴持恭.水力学(上册)[M].北京:高等教育出版社,2007:278-289. [4] 毛昶熙.闸坝泄流局部冲刷问题(三)——冲刷与消能扩散的关系[J].人民黄河,1988(5):65-70. [5] 傅铭焕,梁 锋,郭曙啸,等.渐扩式水跃跃后水深的计算[J].人民黄河,2016,38(9):107-110. [6] 宁利中,宁碧波,田伟利,等.矩形扩散水跃方程的近似解[J].西安建筑科技大学学报(自然科学版),2013,45(6):875-879. [7] 水利部天津水利水电勘测设计研究院.SL253-2000溢洪道设计规范[S].北京:中国水利水电出版社. [8] 吴宇峰,伍 超,刘小兵.渐扩散水跃跃长的研究[J].水科学进展,2007,18(2):210-215. [9] 于志忠.矩形扩散水跃的计算方法[J].水利学报,1989(2):39-45. [10] 吴宝琴,张志恒.矩形扩散水跃水力计算新公式[J].水利水电工程设计,2001,20(2):42-44.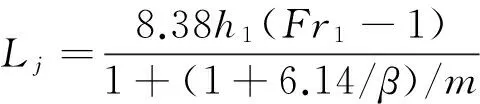

2 渐扩式水跃长度的新公式
3 结 语
