矩形平底明渠水跃长度公式的分析与应用

张志昌，赵 莹，傅铭焕

(西安理工大学 水利水电学院，陕西 西安 710048)

水跃长度是消力池长度设计的重要依据，自1818年贝登对水跃现象开展研究以来，水跃长度一直是该领域研究的热点问题之一。1957年，Bradley等[1]对矩形断面的水跃长度进行了研究，试验的水槽宽度为0.305～1.500 m，跃前断面弗劳德数为1.70～19.55，这是目前水槽宽度和弗劳德数范围最大的研究成果，但该研究是以图和表的形式给出的。1964年，陈椿庭[2]分析了12个人的研究成果，根据Bradley等[1]的试验资料，给出了2个水跃长度经验公式。1979年，张长高[3]根据不可压缩液体恒定均匀紊流基本方程，得出了平底矩形明渠水跃长度的基本计算公式，并在分析前人研究成果的基础上，提出了水跃长度的半经验公式。1965年，Rajaratnam[4]提出可以根据附壁射流的研究成果对水跃进行研究，并进一步测量了水跃区的流速分布、壁面阻力和边界层的发展，为水跃的研究提供了一种新的方法。众多研究者中，Rajaratnam[4]和Hager等[5]将水跃的长度分为水跃长度和旋滚长度，为水跃长度的分类奠定了基础。

虽然许多学者对水跃长度进行过研究，但由于水跃区水流的脉动性及水流条件的复杂性，至今尚未得出水跃长度的理论公式，现今采用的多是根据试验资料总结出的图表或经验公式。目前已有数十个经验公式，但这些公式得出的水跃长度相差较大，这给消力池长度的正确设计带来了困难。为此，本研究根据Bradley 等[1]弗劳德数为1.7～19.55、Hughes等[6]弗劳德数为2.53～6.95、Francesco等[7]弗劳德数为1.87～7.67以及笔者弗劳德数为4.2～8.0的模型试验资料，对现有的水跃长度计算公式进行归纳分类，以期提出矩形平底明渠水跃长度和旋滚长度的新的计算方法，进而为水跃计算公式的选择提供参考。

1 水跃长度计算研究的现状

作者收集的计算水跃长度的经验公式有43个，其中部分公式因年代久远找不到原始文献，是从其他研究者的文章中转引而来的。按照各种公式涉及的计算参数，可将这些公式分为4种类型：Ⅰ是以跃后水深表示的水跃长度公式；Ⅱ是以跃前、跃后水深表示的水跃长度公式；Ⅲ是以跃前断面的弗劳德数与跃前或跃后水深表示的水跃长度公式；Ⅳ是采用其他方法表示的水跃长度公式。43个水跃长度计算公式及其分类如表1所示。由表1可以看出，对第Ⅰ种类型，即以跃后水深表示的5个公式，在跃后水深h2相同的情况下，Bradley等[1]公式计算值最大，Douma[8]公式计算值最小，最大值是最小值的2.03倍。

Bradley等[1]在宽度为0.305 m的水槽中进行了水跃长度的试验，试验的弗劳德数为2.20～7.62，得到的水跃长度为73.20～253.15 cm。根据Bradley等[1]的试验资料，对表1中的第Ⅱ、Ⅲ、Ⅳ种类型的水跃长度公式分析如下。

表1 43个水跃长度计算公式的汇总及分类

第Ⅱ种类型，即表1中以跃前、跃后水深表示的12个公式，其中Posey[8]的公式Lj=(4.5～7.0)×(h2-h1)，由于其取值范围不好确定，在此不做分析；Gini[8]和Smetana[8]的公式形式一样，系数差别仅为0.02，故以Gini[8]公式为代表，与其他9个公式进行分析。以跃前断面弗劳德数Fr1为横坐标，以水跃长度与跃前断面水深的比值Lj/h1为纵坐标，将该类型10个公式的计算结果绘于图1。由图1可以看出，当弗劳德数为7.62时，Walker[8]公式计算值最大，Шаумян[3]公式计算值最小，前者为后者的1.72倍；当弗劳德数为2.57时，Walker[8]公式计算值仍最大，Павловский[8]公式计算值最小，前者为后者的1.57倍。

第Ⅲ种类型，即以跃前断面的弗劳德数和跃前或跃后水深表示的21个公式，其中李炜2[12]公式因超出本研究分析的弗劳德数范围而不做考虑，陈椿庭的2个公式依据的是同一试验资料，故采用表1中陈椿庭1[2]公式。对此类所选择的19个公式的分析结果见图2。由图2可以看出，当弗劳德数为 7.62 时，Silvester[19]公式计算值最大，Пиκалов[11]公式计算值最小，前者为后者的1.52倍；当弗劳德数为2.57时，刘沛清[16]公式计算值最大，基谢列夫1[14]公式计算值最小，前者为后者的1.68倍。

图1 以跃前、跃后水深表示的水跃长度公式的比较

第Ⅳ种类型，即其他方法表示的5个公式，其中基谢列夫2[20]计算公式计算的水跃长度值很大，远远超出了其他公式的计算范围，也远远超出了试验范围，在比较时未予考虑。其他4个公式的计算结果见图3。从图3可以看出，芦丁[8]的公式反映的规律与其他公式相反，即随着弗劳德数的增大相对水跃长度减小；当弗劳德数为7.62时，Воrдаиов[3]公式的计算值最大，Einwachter[8]公式的计算值最小，前者为后者的1.64倍；当弗劳德数数为2.57时，Knapp[8]公式的计算值最大，Einwachter[8]公式的的计算值最小，前者为后者的1.79倍。

1964年，陈椿庭[2]收集了国内外12个水跃长度计算公式，点绘了Fr1与Lj/h1的关系,如图4所示。图4还点绘了Bradley等[1]的6个水槽试验结果。由图4可以看出，各种公式的计算结果与试验结果相差较大，例如当Fr1=10时，最大的Lj/h1是最小的2.2倍；当Fr1=16时，最大的Lj/h1是最小的2.3倍。

图3 以其他方法表示的水跃长度公式的比较

由以上分析可以看出，目前对水跃长度的计算尚存在着较大的差异。产生这种差异的原因固然与水跃区水流的紊动特性有关，例如水跃的脉动特性、跃后位置摆动的不固定性等，更重要的是不同的人对水跃长度位置的判断存在不同的看法。Αгроскин[11]认为，跃尾断面应位于下游的缓流中，水跃长度应根据水跃扩散区内的流速分布规律来确定；Bradley等[1]认为，对水跃长度的观测是困难的，水跃长度跃尾断面的位置可以选择在紧靠旋滚末端的下游断面或较高的底流速开始脱离槽底位置的较远的一个。陈椿庭[2]将前人的研究成果归纳为以下3种情况：一是从水面观测，取水跃旋滚的末端或回流的终止点距跃前断面的距离为水跃长度；二是从底流观测，取较高流速的底流开始脱离槽底的位置距跃前断面的距离为水跃长度；三是将跃后流速分布为明渠正常流速分布的断面距跃前断面的距离作为水跃长度。

正是由于对水跃末端位置的认识不同，不同学者根据自己对水跃长度的理解进行观测，得出了不同的经验公式，这是造成公式差异的主要原因。另外水跃区水流的紊动特性也是造成水跃长度不确定的重要因素，Bradley等[1]在进行水跃试验时认为，水跃长度重复观测值的差异在5%以内都是很困难的。

2 水跃长度的分类

2.1 水跃长度和旋滚长度的定义

水跃长度理解、测量及计算中存在的较大差异，给工程设计中如何选择水跃长度的计算方法带来了一定的困难，本研究试图通过对水跃长度的分类，探求适合工程设计的水跃长度计算公式。

1965年，Rajaratnm[4]就将水跃分为旋滚长度Lr和水跃长度Lj，其将旋滚长度定义为跃首到水跃表面旋滚末端之间的水平距离，将水跃长度定义为跃首至跃后水深约等于尾水水深断面之间的水平距离，约为1.43倍的旋滚长度。1984年，Hughes等[6]也将水跃长度分为旋滚长度和水跃长度，其定义与Rajaratnm[4]相同，并认为水跃长度的定义与Bradley等[1]水跃长度的试验资料一致。1987年，Bretz[15]认为水跃长度应该有2种定义，一种是以水跃的旋滚末端确定的长度为旋滚长度Lr，另一种是以旋滚后水面基本与渠底平行时的最近点确定的长度为水跃长度Lj，并给出了旋滚长度的公式为：

Lr=(6.29Fr1-3.59)h1。

(1)

1990年，Hager 等[5]给出了旋滚长度的计算公式为：

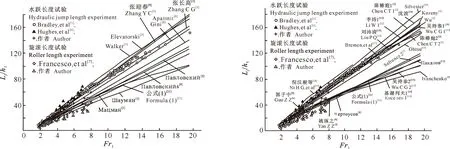
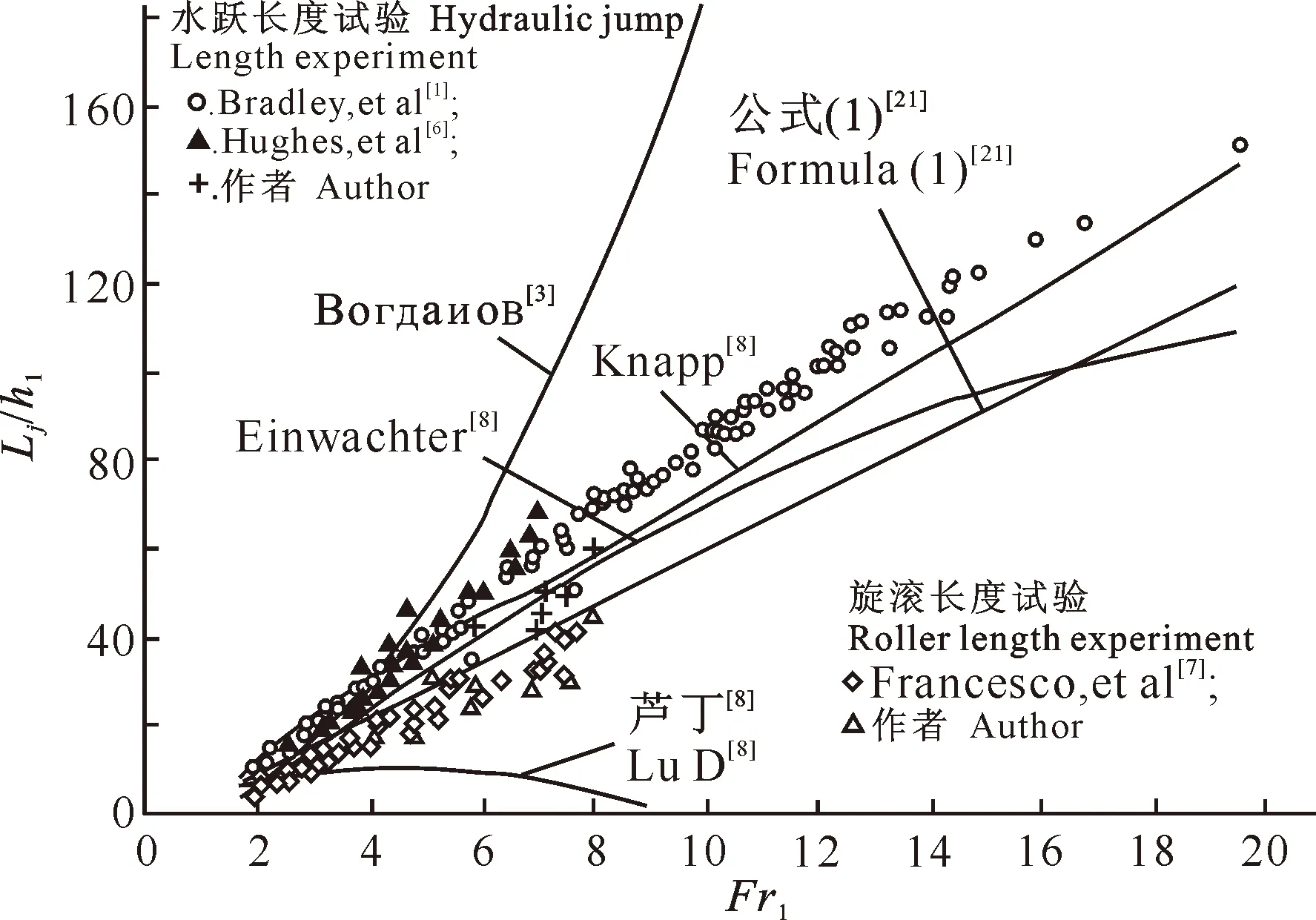
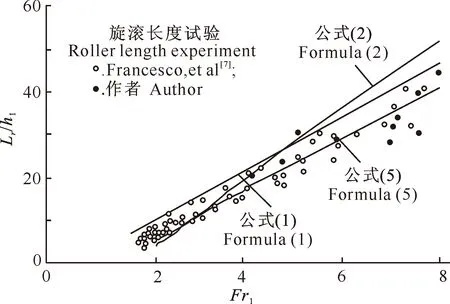
Lr=8(Fr1-1.5)h1，2.5

(2)

1991年，Hager[21]又对旋滚长度进行了进一步研究，给出的计算公式为：

Lr=[160 tanh(Fr1/20)-12]h1，Fr1<15,h1/b<0.1；

(3)

Lr=[100 tanh(Fr1/20)-12]h1，Fr1<15,0.1

(4)

式中:b为水槽(即消力池)宽度。作者分析了以上4个旋滚长度的计算公式，其中公式(3)和公式(4)因涉及到消力池宽度而不易比较，故在分析旋滚长度中不考虑采用。公式(1)公式(2)相比，在弗劳德数较小时，公式(2)计算的旋滚长度小于公式(1)，而在弗劳德数较大时，公式(2)计算的旋滚长度大于公式(1)，且公式(2)计算的旋滚长度曲线斜率与试验点的变化趋势相差较大，而公式(1)计算的旋滚长度曲线斜率与试验点的趋势基本一致。由于目前旋滚长度的计算公式很少，故在旋滚长度的比较中采用公式(1)。

以上研究对水跃长度和旋滚长度的分类具有重要的借鉴意义，可以根据这种分类来研究不同情况下的水跃长度，从而找出适合工程需要的计算公式。表1所列的43个水跃长度计算公式，由于未准确区分水跃长度和旋滚长度的关系而混淆了水跃长度的概念，从而对其应用产生了困难。

2.2 以跃后水深表示的水跃长度计算公式的比较

以跃后水深表示水跃长度的计算公式的计算结果见图5。

图5的数据来自于Bradley等[1]、Hughes等[6]、Francesco等[7]和作者的模型试验，其中旋滚长度用公式(1)计算。计算结果与Bradley等[1]、Hughes等[6]和作者的水跃长度试验结果接近的为水跃长度；计算结果与Francesco等[7]和作者的旋滚长度试验结果以及公式(1)计算结果接近的为旋滚长度。可以看出，Bradley等[1]、Page[8]公式的计算结果与水跃长度的试验数据接近，而Safranez 1[3]公式的计算结果与旋滚长度接近，Safranez 2[8]公式的计算结果介于旋滚长度与水跃长度之间，Douma[8]公式的计算结果远小于旋滚长度。

2.3 以跃前、跃后水深表示的水跃长度计算公式的比较

图6是以跃前、跃后水深表示的水跃长度计算公式的计算结果与试验资料和公式(1)旋滚长度计算结果的比较。由图6可以看出，张长高[3]、Gini[8]的公式与Bradley等[1]、Hughes等[6]及作者的水跃长度模型试验结果比较接近，而Павловскйиs[8]的计算结果与旋滚长度模型试验结果接近，Аравин[8]和Павловский[8]公式介于旋滚长度与水跃长度之间。Walker[8]、Elevatorski[3]、张迎春[9]的公式计算的Lj/h1值大于Bradley等[1]、Hughes等[6]和作者的水跃长度模型试验结果，而Мацман[3]和Шаумян[3]的计算结果略大于旋滚长度模型试验值，但小于公式(1)的计算值。

2.4 以跃前断面的弗劳德数和跃前或跃后水深表示的水跃长度计算公式的比较

图7是以跃前断面的弗劳德数和跃前或跃后水深表示的水跃长度计算公式计算结果与试验结果及公式(1)旋滚长度计算结果的比较。由图7可以看出，陈椿庭1[2]、陈椿庭2[2]、吴持恭1[10]、Bremen等[17]、郭子中[8]以及李炜1[12]公式与Bradley等[1]、Hughes等[6]和作者的水跃长度模型试验结果比较接近，而Safranez 3[3]的计算结果与公式(1)计算的旋滚长度接近，Ohtsu[15]和吴持恭2[13]公式的计算结果介于旋滚长度与水跃长度之间。Wu[2]、Kozeny[3]、沈波[18]、Silvester[19]、刘沛清[16]和倪汉根等[15]公式的计算结果大于Bradley等[1]、Hughes等[6]和作者的模型试验结果，而Iνаnchenko[8]、姚琢之[8]、基谢列夫1[14]、Чертоусов[8]和Пиκалов[11]公式计算值均略大于旋滚长度的试验值，但小于用公式(1)计算的旋滚长度。

图6 以跃前、跃后水深表示的水跃长度计算公式Lj/h1计算值与试验数据的比较

2.5 其他方法表示的水跃长度计算公式的比较

图8是以其他方法表示的水跃长度计算公式计算结果与试验结果和公式(1)旋滚长度计算结果的比较。由图8可以看出，Вогдаиов[3]的计算值过于偏大，远大于水跃长度的试验值；Einwachter[8]和Knapp[8]的公式介于旋滚长度与水跃长度之间；芦丁[8]公式计算的Lj/h1随着弗劳德数的增加而减小，与其他公式的规律不同。

由以上分析可以看出，水跃长度与Bradley等[1]、Hughes等[6]与作者的模型试验资料比较接近的有Bradley等[1]、Page[8]、张长高[3]、Gini[8]、Smetana[8]、陈椿庭1[2]、陈椿庭2[2]、吴持恭1[10]、Bremen等[17]、郭子中[8]公式以及李炜[12]的2个公式；与经验公式(1)计算的旋滚长度接近的公式有Safranez 1[3]、Safranez 3[3]和Павловскйиs[8]公式；介于水跃长度和旋滚长度之间的有Safranez 2[8]、Аравин[8]、Павловский[8]、Ohtsu[15]、吴持恭2[13]、Einwachter[8]和Knapp[8]的公式；大于Bradley等[1]、Hughes等[6]和作者的水跃长度模型试验资料的有Walker[8]、Elevatorski[3]、张迎春[9]、Silvester[19]、Wu[2]、Kozeny[3]、沈波[18]、刘沛清[16]和倪汉根等[15]的公式；小于旋滚长度的公式有Douma[8]公式；Мацман[3]、Шаумян[3]、Iνаnchenko[8]、姚琢之[8]、基谢列夫1[14]、Чертоусов[8]和Пиκалов[11]公式的计算结果略大于旋滚长度试验结果，但小于用公式(1)计算的旋滚长度。与试验规律相反的是芦丁[8]公式。

图8 以其他方法表示的水跃长度计算公式Lj/h1计算值与试验数据的比较

在以上公式中，陈椿庭[2]和吴持恭[10,13]所依据的资料来自Bradley等[1]的试验资料，Bremen等[17]的公式与Bradley等[1]的试验资料基本吻合，张长高[3]公式的数据来源于前苏联学者的试验资料(弗劳德数为1.702～18.450)，与Bradley等[1]试验的弗劳德数(1.70～19.55)比较接近。作者分析张长高[3]的公式，发现其计算结果与所使用的资料误差较大，平均误差为33.5%，而与Bradley等[1]的试验资料比较接近，误差仅为5.37%。因此认为张长高在分析其公式的系数时，参考了Kozeny[3]、Elevatorski[3]、吴持恭1[10]和陈椿庭[2]等人的公式，所得结果反而与Bradley等[1]的试验资料基本一致。由于Bradley等[1]和张长高[3]所使用资料的弗劳德数范围较大，所以建议在设计消力池时，自由水跃长度使用陈椿庭[2]、吴持恭1[10]、Bremen等[17]和张长高[3]的公式计算。对于旋滚长度，由于计算公式较少，下面根据Francesco等[7]和作者的模型试验资料重新分析给出。

3 旋滚长度和水跃长度计算的新公式

3.1 旋滚长度

2007年，Francesco等[7]在粗糙壁面水跃的研究中，为了对比同时测量了光滑壁面水跃的旋滚长度，测量的弗劳德数为1.87～7.67，共有72组数据。作者也进行了旋滚长度的模型试验，共有10组数据。用这82组数据对公式(1)和公式(2)进行验证，结果如图9所示。可以看出，公式(1)和公式(2)与试验点偏离较大，公式(1)的平均误差为42.44%，公式(2)的平均误差为19.57%。为了提高计算精度，根据Francesco等[7]和作者共82组试验数据，重新拟合得到旋滚长度的计算公式为：

Lr=5.450 6(Fr1-1)1.037 6h1，1.82

(5)

将公式(5)的计算值也列于图9进行比较，可以看出，该公式的计算精度高于公式(1)和公式(2)，平均误差为11.38%。

3.2 水跃长度

根据Bradley等[1]于1957年得到的水跃长度试验的117组数据，以及1984年Hughes等[6]水跃长度试验的30组数据和作者水跃长度模型试验的10组数据，绘制Fr1-1和Lj/h1关系图，结果如图10所示。由图10可以看出， 在弗劳德数相同的情况下，Hughes等[6]与Bradley等[1]的试验结果是基本一致的。因此重新对水跃长度进行分析，拟合关系式为：

Lj=10.55(Fr1-1)0.941 6h1，1.7

(6)

经分析，上式的平均误差为5.05%。

水跃长度还可以用下式计算，即：

Lj=7.425 7(h2-h1)(Fr1-1)-0.054 8，1.7

(7)

公式(7)的平均误差为4.5%。

图9 旋滚长度计算值与试验结果的比较

比较公式(5)和公式(6)，可得水跃长度和旋滚长度之间的关系为：

Lj=1.936Lr(Fr1-1)-0.096。

(8)

经计算，在弗劳德数为1.82～7.67时，水跃长度是旋滚长度的1.973～1.614倍。可见弗劳德数越小，水跃长度与旋滚长度的比值越大。

图10 水跃相对长度Lj/h1与(Fr1-1)的关系

4 结 论

本研究对国内外的43个水跃长度公式进行归纳整理，按照Bradley等[1]、Hughes等[6]、Francesco等[7]和作者对水跃长度和旋滚长度的试验资料以及公式(1)对43个公式进行了分类，认为与Bradley等[1]、Hughes等[6]和作者的水跃长度试验结果比较符合的为水跃长度公式，与Francesco等[7]和作者的旋滚长度试验结果以及公式(1)计算结果比较符合的为旋滚长度公式。分析表明，43个公式中，有12个公式的计算结果与Bradley等[1]、Hughes等[6]和作者的水跃长度试验结果吻合，可以作为水跃长度公式；有3个公式基本符合Francesco等[7]和作者的旋滚长度试验结果以及公式(1)的计算结果；其余大多数公式计算结果介于水跃长度和旋滚长度之间，但也有少数公式水跃长度的计算值大于Bradley[1]、Hughes等[6]和作者水跃长度的试验结果，或小于Francesco等[7]和作者旋滚长度的试验结果以及公式(1)的计算结果；而芦丁[8]公式与试验结果相差较大。显然，小于旋滚长度的公式在工程上应用是不安全的，为此推荐陈椿庭[2]、吴持恭1[10]、Bremen等[17]、张长高[3]以及作者提出的计算水跃长度的新公式为消力池自由水跃长度的计算公式，这几个公式适用的弗劳德数为1.70～19.55。对于旋滚长度，推荐采用作者提出的公式(5)进行计算。另外，本研究还分析了水跃长度和旋滚长度之间的关系，表明在弗劳德数为1.82～7.67时，水跃长度是旋滚长度的1.973～1.614倍。

[参考文献]

[1] Bradley J N,Peterka A J.The hydraulic design of stilling basins:hydraulic jump on a horizontal apron(BASIN 1) [J].Journal of the Hydraulic Division,1957,83(5):1-19.

[2] 陈椿庭.平底槽二元水跃长度公式的比较 [J].水利水电技术,1964(4):34-38.

Chen C T.Comparison of hydraulic jump length dyadic formulas in flat bottom flume [J].Water Resources and Hydropower Engineering,1964(4):34-38.(in Chinese)

[3] 张长高.平底矩形明槽中完整水跃的长度 [J].合肥工业大学学报:自然科学版,1979(1):15-34.

Zhang C G.The hydraulic jump length of horizontal bottom and rectangular cross-section [J].Journal of Hefei University of Technology:Natural Science Edition,1979(1):15-34.(in Chinese)

[4] Rajaratnam N.The hydraulic jump as a wall jet [J].Journal of the Hydraulic Division,1965,91(5):107-132.

[5] Hager W H,Bremen R,Kawagowshi N.Classical hydraulic jump:Length of roller [J].Journal of Hydraul Res,1990,28(5):591-608.

[6] Hughes W C,Ernest Flack J.Hydraulic jump properties over a rough bed [J].Journal of Hydraulic Eng,1984,110:1755-1771.

[7] Francesco G C,Vito F,Vincenzo P.Hydraulic jumps on rough beds [J].Journal of Hydraulic Eng,2007,133(9):989-999.

[8] 郭子中.消能防冲原理与水力设计 [M].北京:科学出版社，1982:348-374.

Guo Z Z.Principle of energy dissipation and hydraulic design [M].Beijing:Science Press,1982:348-374.(in Chinese)

[9] 张迎春.自由临界水跃长度的探讨 [J].中国农村水利水电,1997(10):38-41.

Zhang Y C.Study on the length of free and critical hydraulic jump [J].China Rural Water and Hydropower,1997(10):38-41.(in Chinese)

[10] 吴持恭.水力学(上册) [M].北京:高等教育出版社，2008:284.

Wu C G.Hydraulics(One volumes) [M].Beijing:Higher Education Press,2008:284.(in Chinese)

[11] 阿格罗斯金.水力学(下册) [M].清华大学水力学教研组,天津大学水力学教研室,译.上海:商务印书馆,1954:537-539.

Αгроскин.Hydraulics(Two volumes) [M].Hydraulics Department of Tsinghua University,Hydraulics of Tianjin University translated.Shanghai:The Commercial Press,1954:537-539.(in Chinese)

[12] 李 炜.水力计算手册 [M].2版.北京:中国水利水电出版社,2007:107-108.

Li W.Handbook of hydraulic calculations [M].2nd edi.Beijing:China Water & Power Press,2007:107-108.(in Chinese)

[13] 吴持恭.明渠水力学 [M].上海:龙门联合书局,1952:86.

Wu C G.Hydraulics of open channels [M].Shanghai:Longmen Joint Press,1952:86.(in Chinese)

[14] 基谢列夫.水力学-流体力学原理 [M].北京:水利电力出版社,1983:250-254.

Киселев.Hydraulics-principle of fluid mechanics [M].Beijing:Water Resources and Electric Power Publishing House,1983:250-254.(in Chinese)

[15] 倪汉根,刘亚坤.击波,水跃,跌水,消能 [M].辽宁大连:大连理工大学出版社,2008:134-139.

Ni H G,Liu Y K.Shock wave,hydraulic jump,hydraulic drop and energy dissipation [M].Dalian,Liaoning:Dalian University of Technology Press,2008:134-139.(in Chinese)

[16] 刘沛清.矩形明渠水跃段速度分布的理论分析 [J].水利学报,1993(9):48-54.

Liu P Q.Theoretical analysis on rectangular open channel velocity distribution in hydraulic jump region [J].Journal of Hydraulic Engineering,1993(9):48-54.(in Chinese)

[17] Bremen R,Hager W H.T-jump in abruptly expanding channel [J].Jour of Hy Res,1993(1):61-78.

[18] 沈 波.水跃跃长理论研究 [J].重庆交通学院学报,1998,17(3):98-101.

Shen B.Theoretical study on hydraulic jump length [J].Journal of Chongqing Jiaotong Institute,1998,17(3):98-101.(in Chinese)

[19] Richard H.Open-channel hydraulics [M].New York:Mcgraw-hill Book Company,1985:89-91.

[20] 基谢列夫.水力学计算手册 [M].北京:电力工业出版社,1957:321-323.

Киселев.Handbook of hydraulic calculations [M].Beijing:Electric Power Industry Press,1957:321-323.(in Chinese)

[21] Hager W H.Impact hydraulic jump [J].Journal of Hydraulic Res,1994,120:633-637.