基于虚拟目标的导弹越肩发射初制导轨迹优化*

金一欢,雷叶红,冯　昊,彭继平,田　野

0　引　言

大离轴角发射的导弹制导一般可分为初制导阶段和末制导阶段两个阶段.大离轴发射后，初制导应当完成导弹的快速转弯，减小离轴角，从而进入末制导阶段.大离轴发射制导律设计方法大致分为两类，一类是改进比例导引形式，另一类是将制导律设计问题看作优化问题，采用求解最优控制问题的方法求解制导律.

文献[1-3]通过在传统的比例导引律中引入减小离轴角的补偿项，改进了传统比例导引律，具有良好的导引性能.文献[4]基于最优控制的思想设计在线次优全向攻击导引律，在大离轴角情况下具有不错的导引特性.文献[5]通过对导弹转弯特性分析，设计出实时制导律，满足了越肩发射转弯末速和姿态角需求.但是越肩发射初期，导弹只装订发射时目标的位置和速度信息，导引头无法获取目标信息时，实时计算的制导律存在缺少信息的难题.文献[6]将转弯时间作为优化指标，完成转弯的最优轨迹规划，比较了不同初始速度转弯时间；文献[7]将转弯完成导弹末速作为优化指标，设计了最佳推力角.以上文献并没有对转弯完成后的弹轴指向进行讨论.程序导引作为初制导段导引方式，应为末制导段提供良好的交班条件，研究初制导转弯后的弹轴指向具有重要的意义.

通常，越肩发射初期，目标未进入导引头视场角，导弹需利用程序指令完成转弯.本文引入虚拟目标，研究了存在攻角约束的转弯轨迹，分析了虚拟目标位置、空域及速度对指令的影响.对所提出的基于虚拟目标的三段式导引指令进行了三通道仿真验证.

1　问题描述

1.1　导弹动力学模型

本文将直接力引流装置作为执行机构.装备直接力引流装置的导弹模型见图1所示，图1中l为直接力作用力臂，直接力装置阀门可开关控制.俯仰方向设置两个大推力引流喷管3和6，控制弹体俯仰.4个小推力喷管(1,2,4,5)稳定弹体的偏航和滚转通道.

图1　直接力执行机构位置Fig.1　The position of direct force actuator

假设目标在导弹俯仰平面内，导弹通过控制俯仰通道完成转弯，为了简化模型提出如下假设：

1) 转弯过程中，侧向状态量恒为0；

2) 推力以及质量流率为常值；

3) 直接力引流装置产生推力；

4) 转弯过程中，设高度为常值；

5) 控制量u为[-1,1]之间连续控制输入.

基于上述假设，选取攻角、俯仰角、俯仰角速度、速度和质量作为研究变量，可获得导弹俯仰通道动力学模型如下：

(1)

式中：α、θ、ϑ分别为攻角、弹道倾角、俯仰角;P、Fx、Fy分别为发动机推力、空气阻力与升力;m为弹体质量；v、ωz分别为弹体速度和俯仰角速度；Maz为气动力矩在弹体系轴方向投影；Tz为3,6喷管产生的直接力；l为直接力作用力臂；Jz为弹体绕z1轴的转动惯量；c1、c2为正常数；u为[-1,1]之间连续控制输入.

1.2　弹目相对运动模型

程序指令转弯过程中不接收目标信息，需在模型中引入虚拟目标.假设：载机能够预测目标8s内惯性系下的运动轨迹，将目标预测轨迹以及弹道优化轨迹进行对比，预测转弯完成后指向误差，取指向误差最小时目标位置为虚拟目标位置.将虚拟目标位置代替目标实时位置后，二维平面内弹目追逐微分方程组简化为下式

(2)

式中，qε、r分别为视线高低角即弹目连线与水平面夹角和弹目相对距离，初值由虚拟目标位置确定.

1.3　约束条件

为了获得导弹转弯的最优程序指令，需要设计优化函数以及约束条件[8].为使导弹速度矢量尽快指向目标，设置目标函数如式(3)所示

(3)

式中η为导弹速度矢量高低前置角，二维平面内计算公式为η=qε-θ.

为保证导弹在飞行过程中受控，攻角和速度要求满足一定约束.考虑到与末制导段交班时导弹的机动和攻击能力，初制导结束时速度与攻角应满足一定的约束.根据以上要求，设置约束条件如下：

(4)

式中tf为转弯结束时刻.

结合目标函数、约束条件和导弹模型，可求解最优控制指令.状态受约束的最优控制问题的解析解一般很难获得，可利用数值方法求解最优控制问题.求解最优控制问题的数值方法一般分为间接法和直接法.高斯伪谱法是直接法的一种，与间接法相比具有不需要估计协态变量的优点[9-10].文献[11]基于最优中制导律问题，将高斯伪谱法与比例导引、打靶法进行了比较，仿真结果表明综合考虑计算精度和计算效率等因素，高斯伪谱法具有明显优势.

2　数值仿真及分析

2.1　高斯伪谱法

高斯伪谱法的基本原理是在Legendre-Gauss配置点上离散状态变量和控制变量，并以离散点为节点构造Lagrange插值多项式来逼近状态变量和控制变量.通过对全局插值多项式求导来近似状态变量的导数，从而将微分方程约束转换为一组代数约束.

引入新的时间变换t=(τ+1)tf/2,将时间区间[0,tf]变换到[-1,1].将状态变量x(τ)用Lagrange插值多项式Li(τ)(i=0,1,…,N)逼近，即

(5)

(6)

式中,

x(τ)在LG点的导数可通过微分矩阵近似为：

(7)

式中,Dki为N×(N+1)维微分矩阵，其中元素为

(k=1,2,…,N;i=0,1,…,N)

利用上式，连续系统的状态方程被离散为代数方程

(8)

这里状态方程仅在LG点配置，边界点变量X0由初始条件确定，Xf和Uk由高斯积分确定，如式(9)所示

(9)

式中，ωk为高斯积分权值.

可利用高斯积分，求取性能指标，如式(10)

(10)

端点约束为：

G(X0,Xf)=0

(11)

状态约束沿LG点离散为

C(Xk,Uk)≤0(k=1,2,…,N)

(12)

基于以上对状态量和控制量的离散，得到可用于非线性规划求解的代数表达式.

2.2　问题求解

利用非线性规划算法SQP对通过高斯伪谱法获得的非线性规划问题进行解算，初始条件设置如下：

表1　计算初值Tab.1　Initial value for computation

仿真结果如图2.

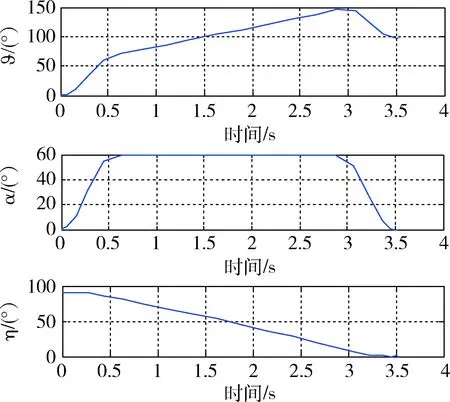
图2　优化结果曲线Fig.2　Results of optimization

导弹速度高低前置角曲线可见，导弹速度矢量前置角在转弯完成时趋于0，满足设计期望.俯仰角曲线图中曲线呈明显的分段特点，由三段斜率不同的线段连接而成.利用攻角曲线对俯仰角曲线特点进行分析可得：第一段为攻角建立期，以最大控制能力快速建立攻角，俯仰角曲线表现为快速增加的特点；第二段为攻角维持期，攻角到达并维持在约束值，俯仰角曲线表现为缓慢增加特点；第三段为攻角回落期，该阶段导弹速度高低前置角趋于0，攻角回零.俯仰角在这一阶段为负斜率曲线.本文将利用三段式特点，设计俯仰角指令.为了说明三段式指令的特点，取指数指令ϑc=ϑf·(1-e-at)进行仿真对比，式中ϑf=138°,a=1.单通道数值仿真结果如下图：

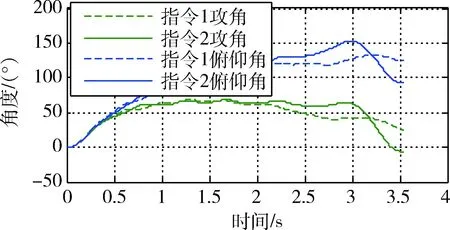
图3　俯仰角与攻角仿真结果对比图Fig.3　Pitch angles and angles of attack under exponent command and three-segment command

图3中指令1为指数指令仿真结果，指令2为三段式指令仿真结果.到位角误差分别为：指令1为0.332°，指令2为0.006°.图中指令1的攻角曲线在转弯完成时没有收敛到0附近，指令2在转弯完成时攻角收敛到0附近.可见指令2的形式具有良好的攻角回零效果.

2.3　初值影响分析

不同初始高度条件下，计算所得俯仰角指令见图4.对比不同曲线可见，随着高度的增加，转弯完成所需时间增加.在攻角建立期，不同高度的俯仰角指令上升斜率一致.在攻角维持期时，发射高度越小的俯仰角指令斜率越大.不同高度的俯仰角指令在攻角回落期下降速度一致.

高度不同的俯仰角指令峰值和终值相差不大，而峰值和终值的时间有显著差异.由图5中曲线变化趋势可见，两个到达时间与高度呈线性相关.利用线性拟合公式，可计算不同高度下的俯仰角指令到达时间.

图6为10 km下不同初始速度俯仰角指令曲线.根据不同速度曲线的变化可知，随着速度的增加，转弯完成所需时间增加.

不同速度下，俯仰角指令峰值和终值相差不大，指令差异主要表现在峰值时间和终值时间.不同初始速度俯仰角指令达到峰值和终值时间曲线如图7所示.

图4　不同高度俯仰角优化结果图Fig.4　Optimal results at different heights

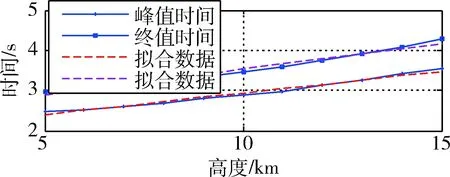
图5　峰值时间和终值时间随高度变化图Fig.5　Chart of peak and final time influenced by height

图6　不同速度俯仰角优化结果图Fig.6　Optimal results with different initial velocity

图7　峰值时间和终值时间随速度变化图Fig.7　Chart of peak and final time influenced byinitial velocity

根据图7可知，随着初始速度增大，到达时间线性增大.

图8给出了不同转弯角度的俯仰角指令曲线.

图8　不同转弯角度俯仰角优化结果图Fig.8　Optimal results with different turning angle

通过分析差异可知，初始离轴角不同影响了转弯指令的峰值时间.当转弯角度小于20°时，俯仰角指令没有出现三段式特点，这是由于转弯角度过小导致转弯时间短，攻角未达到约束值便回零所致.由此可知，本文设计的三段式转弯指令不适用转弯过小的情况.不同俯仰角指令的峰值时间和终值到达时间线性拟合结果如图9.

利用图9，对比数值仿真结果与线性拟合曲线可见，峰值时间和稳定时间与初始视线角呈线性相关.可通过线性插值对不同转弯角度的俯仰角指令进行计算.

2.4　三通道仿真验证

为了验证三段式指令以及以上分析的有效性，

图9　峰值时间和终值时间随转弯角度变化图Fig.9　Chart of peak and final time influenced by turning angle

利用线性插值计算程序指令并进行三通道仿真.三维空间中式(3)可表示为式(13)

(13)

仿真验证时令虚拟目标与导弹速度矢量位于同一水平面，即可验证以上分析内容的准确性.使用结束时攻角α、离轴角σ、速度矢量前置角φ作为评定导引指令好坏的标准，其中离轴角为转弯结束时，弹轴与弹目连线夹角，速度矢量前置角为速度矢量与弹目连线夹角，仿真原理图如图10.

图10　三通仿真流程图Fig.10　Flow chart of three channel simulation

将v0=210 m/s、H0=10 km、qε0=90°作为标准状态.分别利用高度差、速度差和视线角度差对标准状态的俯仰角指令进行修正， 特征时间计算公式如下：

t1=2.877+0.108 1×dH+0.002×dv

t2=3.454+0.129 7×dH+0.002 3×dv

(14)

导引指令计算公式如下：

(15)

式中，tdot为上一线段末点值.为了保证攻角回零，在导引指令后增加0.1 s维持俯仰角指令不变.利用上式计算程序指令，视线角为100°仿真结果如表2.

由三通道仿真结果可见，攻角误差最大值为-6.20°，离轴角误差最大值为8.56°，速度矢量前置角误差最大值为6.38°.一般的红外导引头视场跟踪角为±35°，对比仿真结果可知，本文设计的程序指令可以导引导弹发现目标.

表2　转弯误差Tab.2　Error of the command

2.5　实时误差修正

程序指令对飞行过程中产生的误差并没有修正作用.由于不确定扰动的存在，导弹会逐渐偏离飞行平面，从而降低转弯末端的指向精度.本文基于预测控制的思想，根据预测误差定时调整程序指令以及转弯平面.指令更新步骤如下：

1) 基于导弹当前速度和姿态计算tf内转弯轨迹Cm,tf为转弯剩余时间；

2) 对比Cm与目标预测轨迹CT,预测转弯完成时速度倾角误差Δθc(0);

3) 分别计算转弯完成时间tf-0.1 s,tf+0.1 s的速度倾角误差 Δθc(-1)、Δθc(1);

4) 根据Δθc更新虚拟目标位置与程序指令.利用选定的虚拟目标位置，确定射面，修正导弹转弯指令以及姿态.

由于实际飞行过程中存在模型不确定以及干扰不确定因素，这种建立在实际反馈信息基础上的迭代优化过程，能引入不确定性的影响，并实时修正.通过引入实时更新的算法，使得程序指令在飞行过程中更能适应实际过程.

选取t=2,t=2.5两个时间点对俯仰角指令进行定时修正，初始条件10 km，210 m/s，修正前后误差对比如表3所示.

通过数值仿真可见，定时修正可以使转弯完成时速度矢量前置角误差减小，提高程序指令转弯的抗干扰能力.

表3　误差对比Tab.3　Compare of the results

3　结　论

本文求解了具有攻角约束的空空导弹越肩初制导轨迹规划问题.通过引入虚拟目标，研究了导弹转弯完成后速度矢量指向与转弯指令的关系.轨迹优化结果表明，满足导弹快速转弯以及攻角回零约束的俯仰角指令具有明显的三段式特点.通过分析不同空域、初始速度以及转弯角度的俯仰角指令，发现这三者对指令的影响呈线性.利用分析结果，本文给出了基于虚拟目标的三段式程序指令的计算方法，并利用三通道仿真对导引指令的有效性进行验证.同时，在优化结果的基础上，基于预测控制思想对转弯平面和转弯指令进行在线修正，使得程序指令能够适应实际过程.仿真结果表明本文设计的程序指令效果良好，对空空导弹越肩发射导引指令设计具有一定的参考价值.