类IXV飞行器初期再入制导与姿态控制方法研究*

黄盘兴，何英姿，杨　鸣，郭敏文

0　引　言

“过渡试验飞行器”(intermediate experimental vehicle, IXV)是欧洲未来运载器预备工程(future launch preparatory program, FLPP)框架下研发的再入技术验证试验平台，主要用于验证升力式自主再入飞行器从近地轨道无动力再入返回的高超声速飞行关键技术和关键系统，降低未来可重复使用运载器的研制风险.经过近10年研制，2015年2月11日，IXV在法属圭亚那库鲁航天发射中心由“织女星”(Vega)火箭成功发射，飞行试验取得圆满成功，其为欧洲未来自主研制可重复使用航天运输系统奠定了基础.

IXV的气动外形与再入控制机构不同于传统的再入返回器(包括返回舱、航天飞机类升力体)：其采用无翼升力体设计(如图1所示)，升阻比0.7，兼具有翼升力式飞行器的可控性高和返回舱系统简单的优点；在大气层内采用反作用发动机(RCS)和气动尾襟翼进行混合姿态控制.其中，两片尾襟翼同向偏转可作为升降舵控俯仰，异向偏转作为副翼可控制滚转(横向).再入过程中俯仰、横向通道采用RCS/气动舵复合控制；偏航通道则全程采用RCS进行控制.

IXV需要精确的在海上伞降着陆，需要高精度的制导-控制律作支撑.本文根据类IXV飞行器的再入特性，开展鲁棒性较强的高精度再入制导律与控制律设计研究，为未来先进返回器的研制提供技术参考.

图1　IXV升力体外形Fig.1　The shape of IXV with lifting configuration

1　再入飞行器六自由度运动模型

飞行器在返回坐标系中的质心动力学方程为：

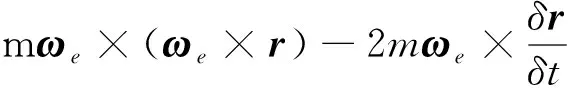
(1)

式中：m为飞行器质量；r为飞行器质心地心距矢量；P是作用在飞行器上的发动机推力矢量；R代表作用在飞行器上的气动力矢量；mg为作用在飞行器上的地球引力矢量；ωe为地球自转角速度.等号右边的后两项分别代表离心惯性力与哥氏惯性力.

本体坐标系上绕质心转动的动力学方程如下：

(2)

2　数值预测-校正制导方法

初期再入制导的任务是给出导引指令将飞行器从再入点导引到下一制导段的交班条件，期间必须满足指定的过程约束与终端约束条件.一般将初期再入制导分为两大类：标称轨迹制导和预测-校正制导.标称轨迹制导简单，适应线性扰动，但落点精度受再入初始误差以及再入过程环境扰动等因素的影响较大.预测-校正制导具有对初始误差不敏感的优点，抗干扰能力与适应性强，且数值预测-校正制导法的制导精度较高.

根据IXV类飞行器的中低升阻比特性，为提高再入任务的灵活性与适应性，初期再入段采用数值预测-校正制导律.采用“离线给定参考攻角剖面，在线生成倾侧角指令”的制导方案，预测-校正制导实现对倾侧角指令的在线调节.

2.1　标称倾侧角剖面设计

飞行器的倾侧角大小剖面由初始下降段、拟平衡滑翔段与常值飞行段组成，如图2所示.

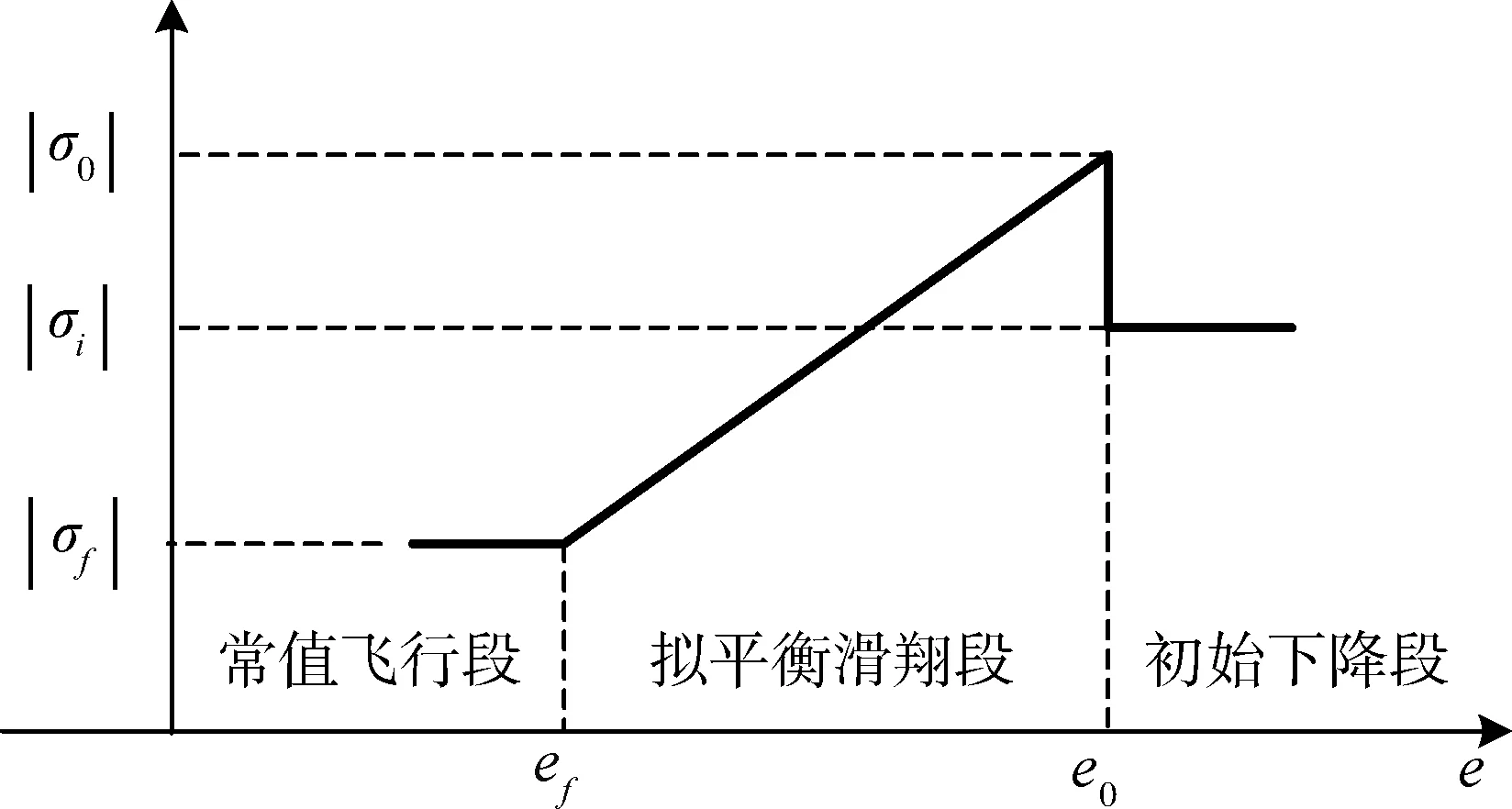
图2　初期再入倾侧角剖面Fig.2　Reentry bank angle profile

在初始下降段飞行器速度大但大气稀薄，倾侧角调节对轨迹影响小，故其大小取为常值σ0,并采用开环制导模式.当飞行器达到拟平衡滑翔边界或指定高度、能量时，进入拟平衡滑翔段，倾侧角剖面|σ|取为能量的线性参数化函数：

(3)

其中：|σ0|为倾侧角剖面的初始值；|σf|是拟平衡滑翔段的末端倾侧角；e为实时的单位质量能量.

在后期飞行引入了常值飞行段是为了避免较大的姿态角速率，能为下一段制导提供较好的交班姿态.

2.2　纵向预测-校正制导

在拟平衡滑翔段，对纵向轨迹的导引采用预测-校正制导算法：每间隔一定制导周期，以当前状态参数为初值，以标称倾侧角(以|σ0|为自变量的剖面)为控制变量，通过积分纵向微分方程得到终端状态(预测)；根据积分得到的终端预测值与期望终端值之间的偏差对倾侧角剖面进行校正.

再入段特定时刻的标称倾侧角剖面形态由剖面的初始值|σ0|唯一确定，在攻角剖面一定的条件下，制导末端剩余航程Stogo(ef)(或末端能量ef(Stogof))为|σ0|的隐函数，纵向再入轨迹规划问题转化为一个单参数搜索问题.以剩余航程为自变量积分纵向微分方程进行数值预测，需要求解的非线性方程为：

f(x)=0

(4)

其中，x表示|σ0|,f(x)表示预测的能量偏差，即预测能量减去期望能量.进行积分的纵向轨迹微分方程为：

(5)

式中：L、D为飞行器受到的升阻力；Δψ为航向角与目标视线角的差值.

式(4)采用牛顿迭代法求解，当过若干次迭代后，仍不能得到收敛解，制导算法将停止该迭代进程，将上一个制导周期的收敛值作为指令输出.

上述制导过程仅匹配了终端约束，未匹配过程约束，需要进一步对σ(V)进行满足过程约束的边界判断：

(6)

2.3　侧向制导

纵向制导仅给出倾侧角σ的大小，倾侧角σ符号由侧向制导决定，控制量为航向角偏差Δψ(也可采用横程)，即采用航向角误差门限Δψthreshold(V)确定倾侧角的符号.航向角偏差Δψ定义为

(7)

其中，(θT,φT)为目标点经纬度.

航向角偏差门限Δψthreshold(V)设计为速度的分段线性函数：

Δψthreshold=

(8)

门限选取原则为既要使再入轨迹满足终端横向位置和角度约束，又要保证滚转反向不过于频繁，易于工程实现.倾侧角符号反转逻辑的数学表达式为：

sign(σi(V))=

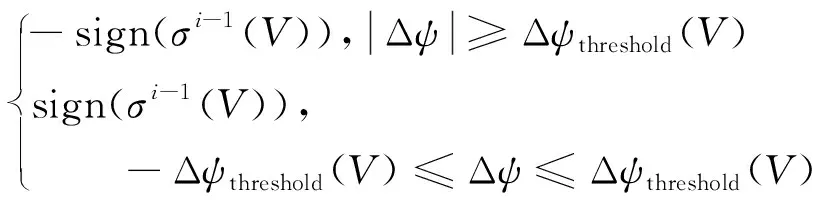
(9)

3　RCS/气动舵组合姿态控制方法

与传统飞行器不同，IXV再入采用RCS与气动尾襟翼混合控制姿态：在再入初期，3通道均采用RCS进行姿态控制；进入稠密大气层后，俯仰、滚动通道采用尾襟翼控制，而偏航通道则仍采用RCS控制.此种控制方案偏航通道的控制能力弱，但也避免了传统方向舵偏转引起的横侧向耦合.

3.1　RCS控制律

飞行器再入初期空气稀薄，气动舵面效率不足，要采用RCS完成俯仰、滚转通道的姿态控制任务.由于初期再入段侧滑角指令为0，无侧滑机动，可全程采用RCS完成偏航通道的控制.

不同于气动舵面的偏转在时域上是连续的，RCS推力器只有开启和关闭两种状态，在时域上是离散的.为此采用基于脉宽调制(PWM)的控制方案：先根据飞行器当前姿态偏差确定所需要控制力矩，再把控制所需力矩调制成不同脉冲宽度的RCS力矩，确定RCS开关时间.

再入初期各通道独立，控制力矩指令生成采用PD控制算法：

(10)

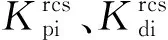
将控制所需力矩调制成不同脉冲宽度的RCS力矩，输出RCS开关时间的PWM调制算法如下：

(11)

Mri为RCS产生的固定力矩，Tsam为控制周期，τi为每个控制周期RCS的开启时间.

为了避免RCS的反复开启，并考虑RCS的最小开启时间限制，引入RCS的控制死区，当RCS离散控制律解算的RCS开启时间小于门限值τdi时，RCS不开启：

(12)

3.2　气动舵面控制律

当飞行器高度下降到60 km以下时，进入高动压区，气动舵面效率较高，可完全采用气动舵面进行俯仰、滚转通道的姿态控制.

针对飞行器模型参数变化剧烈、动力学非线性与不确定性强等问题，采用增益调度测量实现自适应控制，且控制器采用传统的PID控制结构：在控制器设计时选择高度、攻角、马赫数、动压等状态量作为增益变量，在飞行全包络线内将非线性的飞行器模型在不同的配平条件下直接线性化，然后针对每个线性模型设计控制参数，再采用插值策略把各个单独的控制器综合完成飞行器在整个飞行包线内的控制.

飞行器再入攻角大，为使舵面迅速达到标称状态，减小反馈回路的负担，俯仰通道增加前馈环节进行攻角配平.因偏航通道采用RCS控制，执行机构对滚转通道不产生气动耦合，故未设计协调支路，控制结构较为简单.气动舵面姿态控制系统结构如图3所示：

图3　气动舵面姿态控制结构Fig.3　Attitude control block diagram with aerodynamic flaps

基于根轨迹与频域法的传统控制参数设计过程复杂、耗时长，引入积分型LQR进行控制参数的快速设计.一般LQR控制可设计PD控制参数，积分型LQR则将状态偏差量也引入到系统中，可设计PID控制参数[15].采用LQR技术设计控制参数存在的难点在于如何根据系统的实际要求选择加权矩阵的诸元素，Bryson准则虽然是较为有效的方法，但根据其设计出的参数可能不满足系统的时域和频域指标要求.因此，根据时域和频域指标的满足情况进行反馈设计，其设计流程如图4所示：

图4　基于鲁棒伺服LQR的控制参数设计流程Fig.4　Flow chart of control parameters design with robust servo LQR method

3.3　复合控制策略

在整个再入过程中，随着动压增加，气动舵面控制能力由弱到强，因此气动舵面承担的控制负担也随着动压逐渐增大，相应的RCS承担的控制负担随着动压逐渐减弱.由于初期再入段侧滑角指令为0，无侧滑机动，经分析可完全采用RCS完成偏航通道的控制.为了减小舵面偏转带来的气动耦合，初期再入段偏航通道单独使用RCS控制，俯仰通道与滚转通道根据动压条件进行切换控制.

在切换控制过程中应考虑两套执行机构复合控制的控制分配问题，这里采用控制加权的方法实现执行机构的平滑切换：

(13)

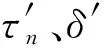
(14)

式中，q1和q2为复合控制阶段的起始、终止动压值，其结合各通道舵效与控制品质要求确定，q为当前动压.

4　数值仿真验证

一类IXV再入飞行器再入初始条件及过程约束、终端约束如表1所示.

飞行器再入飞行过程考虑干扰项，各项干扰均服从均值为0的正态分布.各项干扰的3σ值为：初始速度偏差20 m/s、飞行路径角偏差0.05°、航向角偏差0.1°、高度偏差200 m、东向位置偏差2 km、北向位置偏差2 km；气动力系数偏差15%、气动力矩系数偏差30%；大气密度偏差15%、风干扰的风速50 m/s.RCS最小开启时间10 ms，预测校正制导周期5 s，姿态控制周期0.01 s.

进行1 000次蒙特卡洛打靶仿真.绘制前400条的高度-速度、攻角、侧滑角、倾侧角、三维轨迹曲线，如图5～9所示；末端状态偏差及最大驻点热流、过载的散布如图10所示.

表1　类IXV飞行器再入初始条件及过程约束、终端约束Tab.1　Initialization, trajectory constraints and terminal conditions of a class-IXV aircraft

图5　高度-速度曲线Fig.5　Curves of velocity with height

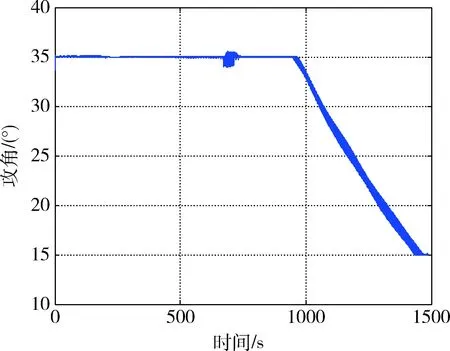
图6　攻角随时间变化曲线Fig.6　Time histories of attack angle

图7　侧滑角随时间变化曲线Fig.7　Time histories of sideslip angle

图8　倾侧角随时间变化曲线Fig.8　Time histories of bank angle

图9　经度-纬度-高度三维曲线Fig.9　The three-dimensional trajectory

图10　末端状态偏差及最大驻点热流、过载散布Fig.10　Deviations of terminal condition errors,and maximal heat rate,maximal aerodynamic load

图5可知飞行器在初始再入过程中有一次较大的跳跃，尔后飞行器达到准平衡飞行状态，高度平滑下降.从攻角、侧滑角、倾侧角曲线可知：因存在气动耦合，倾侧角执行翻转机动时会对俯仰与偏航通道造成影响，尤其是采用舵面进行滚转通道控制时；偏航通道因全程采用RCS进行控制，控制能力较弱，滚转机动时造成的侧滑角控制偏差较大，但控制在±5°以内；再入过程中倾侧角符号翻转不大于4次，经统计其控制偏差小于2°，攻角控制偏差小于1°.

图10表明：末端高度偏差小于1.5 km，速度偏差小于35 m/s，航向角偏差小于4°，剩余航程偏差小于4 km；驻点热流小于5 MW/m2，气动过载小于1.8 g.在各项干扰条件下飞行器满足过程约束要求，且具有较好的制导精度，制导与姿态控制系统的鲁棒性较强.

5　结　论

类IXV飞行器兼具有翼升力式飞行器的可控性高和返回舱系统简单的优点，是未来先进可重复使用返回器的可选方案之一.本文结合类IXV飞行器的再入特点，采用数值预测校正制导策略及俯仰与滚动RCS/气动舵复合控制、偏航全RCS的姿态控制策略完成了其再入飞行制导控制系统的设计及仿真验证.仿真结果表明，在各项干扰条件下，所设计的制导控制律取得了较好的姿态控制精度及制导精度.后续将结合导航方案继续深入研究.