带柔性载荷超静平台的模型参数在轨辨识*

2018-07-12齐田雨张科备

空间控制技术与应用 2018年3期

齐田雨，汤　亮,2，张科备

0　引　言

天基天文观测和极高分辨率对地观测等任务，对航天器光学载荷的指向精度和指向稳定度等性能提出了更高的要求[1-2].主动指向超静平台通过六作动杆的主被动一体控制，实现光学载荷在工作空间范围内的高精度指向.主动指向超静平台具有控制精度高、承载能力强、动态响应速度快等优点，可广泛应用于对地观测和天文观测等极高精度指向领域.

主动指向超静平台模型参数中，作动杆刚度影响系统的固有频率，阻尼参数影响载荷整体的振动衰减速率，这两个参数将影响载荷控制器的稳定性.航天器发射过程中的剧烈振动，及在轨热环境的改变，会引起主动指向超静平台模型参数的变化.在线辨识主动指向超静平台模型参数，可以为载荷控制器设计奠定良好的基础.光学载荷口径变大，柔性特性表现越来越明显，在主动指向超静平台模型参数的辨识中，需要考虑载荷柔性振动的影响.因此有必要研究考虑载荷柔性振动情况下，主动指向超静平台的模型参数辨识方法.

目前国内外对超静平台的研究主要集中在设计控制算法[3-4]和装配结构[5-6]上.对模型参数的分析也有一些研究[7-8].辨识方法上，HUANG[9]等基于卡尔曼滤波和能量平衡原理，实现了多参数(刚度系数、质量和阻尼系数)在线辨识，进行复杂结构构件损伤识别.CHEN[10]提出一种混合优化算法，对六自由度电动液压平行机构的动力学参数进行辨识.WILSON等[11]提出多变量并发递推最小二乘法，用以解决无法直接应用线性回归的未知参数辨识问题.这一算法将单一问题划分为多个独立的线性问题，这些子问题除了包含被辨识参数之外，还包含未知参数.通过为未知参数设定标称值，并在后续并发运行的辨识过程中更新、共享运算结果，实现航天器质量特性的在轨准确辨识.

本文针对带柔性载荷的超静平台模型参数辨识问题，采用多变量并发递推最小二乘辨识方法，实现了超静平台模型参数的在轨辨识，为载荷的控制器设计打下基础.

1　动力学模型的建立

图1给出了带有超静平台和柔性载荷的卫星结构简图，柔性载荷与星体平台之间通过超静平台的6根作动杆连接.

图1　带超静平台的卫星结构简图Fig.1　Satellite structure with ultra-quiet platform

考虑柔性载荷振动的超静平台动力学方程

(1)

2　模型参数辨识的多变量并发递推算法

最小二乘辨识方法通过最小化误差的平方找到对一组数据拟合最佳的函数，已成为动态系统辨识的主要手段.本文中由于式(1)中存在未知的振动模态坐标，无法直接进行递推最小二乘辨识.

2.1　模型参数的最小二乘辨识

改写式(1)，将待辨识模型参数表示为最小二乘辨识的标准形式.

此时，可以将式(1)展开为

(3)

(4)

(5)

(6)

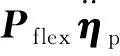
2.2　振动模态的卡尔曼滤波估计

将考虑载荷柔性振动的超静平台动力学模型写成状态方程形式，为

(7)

其中

令

Axf(Kp)=D-1A,Bxf=D-1B

则

(8)

采用差分近似将方程离散化，离散时间Δt,有

(9)

整理得

xkf(k+1)=Φ(k)xkf(k)+G(k)u(k)

(10)

其中

Φ(k)=ΔtAxf(Kp)+E

G(k)=ΔtBxf

同理，观测方程为：

ykf(k)=Ckfxkf(k)

(11)

载荷的转动位移和转动角速度可以通过星敏感器和陀螺直接测量得到.根据测量得到的作动杆长度变化，结合式(2)和动量定理解算得到载荷的平动位移，并通过一次差分得到平动速度.

在获得式(10)～(11)的离散状态方程后，采用卡尔曼滤波方法实现超静平台状态量xkf的准确估计，进而获得柔性载荷振动模态坐标的估计值.

卡尔曼滤波是去除噪声还原真实数据的一种数据处理方法，在测量方差已知的情况下能够从一系列存在测量噪声的数据中，估计动态系统的状态.采用卡尔曼滤波估计超静平台状态量xkf的过程如下：

(12)

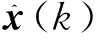
综上所述，得到带柔性载荷的超静平台模型参数辨识的算法流程如图2所示.

1) 根据k时刻模型参数辨识值Kp(k)和Cp(k),更新状态转移矩阵Φ(k+1,k);

图2　辨识算法流程图Fig.2　Identification process

3　仿真分析

仿真参数：载荷质量为mp=1 012.6 kg,三轴主惯量为

[IxIyIz]=[1 434.21 342.8514.8]kg·m2

柔性载荷以相机及其遮光罩为例.柔性载荷的一阶模态是影响超静平台参数辨识精度的主要因素[12].因此在本文计算中，只考虑载荷振动的一阶振动模态对超静平台和载荷组合整体的影响.载荷一阶模态频率为2.92 Hz，模态阻尼比为0.005.柔性载荷相对于超静平台的平动刚柔耦合系数和转动刚柔耦合系数分别为

Ptran=[1.716.61.6]T,

Prot=[16.21.716.1]T

作动杆阻尼系数标称值ci=800 N/(m/s),i=1,2,…,6,即最小二乘递推算法中，辨识初值

作动杆刚度系数标称值为ki=25 728N/m,i=1,2,…,6,即辨识初值

图4给出了辨识过程中作动杆伸长量变化曲线.作动杆位移最大不超过4 mm，在作动器行程允许范围内.

图3　作动杆输入力Fig.3　Input forces of actuators

图4　作动杆行程Fig.4　Displacements of actuators

图5和图6分别给出了考虑与不考虑柔性载荷振动影响的两种模式下，主动指向超静平台模型参数中刚度系数的辨识结果.分析图5和图6的仿真结果可知，考虑柔性载荷振动的多变量并发递推最小二乘法，能够实现超静平台模型参数辨识误差快速收敛，超静平台模型参数辨识误差优于2.22%.而不考虑柔性载荷振动的传统递推最小二乘法，由于柔性载荷振动模态的影响，辨识结果在标称值附近较大范围波动，模型参数辨识相对误差达到15.41%(3σ).

图7中给出了考虑与不考虑柔性载荷挠性振动，和考虑20%刚柔耦合系数误差等3种情况下，超静平台刚度系数辨识的误差对比.仿真结果表明，通过卡尔曼滤波估计柔性载荷一阶模态坐标的变化，能够降低柔性振动对超静平台模型参数辨识的影响，柔性振动耦合系数的变化对辨识精度影响很小.

图5　考虑柔性载荷振动时辨识误差Fig.5　Identification error considering vibration

图6　不考虑柔性载荷振动时辨识误差Fig.6　Identification errors without considerationof vibration

图7　不同耦合系数下辨识误差对比(作动杆1)Fig.7　Identification error under different situations(actuator 1)

不同仿真条件下的辨识结果对比如表1所示.仿真结果表明，本文方法可以充分考虑柔性载荷振动影响，能够快速准确辨识出超静平台模型参数.在考虑20%的刚柔耦合系数误差时，模型参数辨识误差仍优于10.20%(3σ).

4　结　论

本文针对超静平台模型参数在轨辨识精度受到柔性载荷振动影响的问题，建立了考虑柔性载荷振动的超静平台动力学模型，设计了一种考虑柔性载荷振动影响的多变量并发递推最小二乘辨识方法，能够提高超静平台模型参数辨识精度，提高模型参数误差收敛速度，可以实现带柔性载荷的超静平台模型参数高精度辨识.辨识过程中首先利用卡尔曼滤波估计柔性载荷振动模态；其次利用多参数并发递推最小二乘法实现超静平台模型参数辨识，辨识误差优于2.22%.在考虑20%刚柔耦合系数误差时，算法辨识效果仍优于传统递推最小二乘法，验证了本文提出方法的有效性.