高精度星相机光学系统像质评价及实现*

贾永丹, 王伟之,孙　建,王　妍,宗云花,曹桂丽，康少英

0　引　言

星敏感器因具备姿态测量精度明显高于其他姿态敏感器的优势，为空间飞行器的姿态测量开辟了一个新途径[1-2].星相机属于广义星敏感器[3]，用于拍摄、处理星图，与高分辨率对地观测相机进行联合处理，形成用于确定地相机光轴指向的姿态数据，从而提高高分辨率相机影像地面定位精度[4-5].传统星敏感器主要用于卫星姿态控制，需要兼顾动态性能、卫星机动、安全等多种模式和环境的适应性，姿态测量精度一般为几角秒到几十角秒[3].星相机主要配套为高分辨率相机服务，随着地相机光轴指向精度的提高，星相机较星敏感器的测量精度大幅提高，对星相机光学系统设计提出了更高要求.

目前国内外对星敏感器光学系统的研究较多，近年来逐渐对对星相机光学系统的各项指标形成共识[6-10]，但对星相机光学系统像质评价方法和标准不尽相同[3,6,10-12].星相机作为一种角距测量系统，其像点在像面上的位置精度是一个核心指标，从传统点目标及空间成像系统角度考虑能量集中度、畸变、倍率色差、温度稳定性因素基本都有所提及.文献[6]和[10]均未能兼顾考虑色温及温度变化情况下，各项指标的变化.文献[3]认为星点位置精度是光学系统设计时像质评价过程中必不可少的评价方法，尤其是恒星色温及温度变化对该精度的影响，但其未考虑恒星色温及温度变化情况下质心位置与理想像高之间的偏差，即未考虑质心位置畸变；同时对于温度变化的条件也仅限于均匀温升的考虑.然而实际光学系统在轨控温过程中，将不可避免地存在径向梯度温度变化，故光学系统设计过程中还应考虑径向梯度温度对光学系统质心位置精度的影响.

本文针对高精度星相机光学系统的应用需求，从星相机光学系统设计过程中的像质评价方法和标准出发，对星相机光学系统像质评价指标进行分析，并给出设计实例.

1　评价指标分析

1.1　星点质心位置指标分解

在轨/地面对星图进行处理计算星相机姿态信息时，要根据获取的星图提取星点的质心位置信息，星点质心位置的准确性很大程度决定星相机的精度[14].影响星点质心位置确定精度的主要因素包括光学系统设计、星点质心提取精度、地面/在轨标定精度，限于篇幅，后两者不做讨论.

如图1所示，从光学系统角度考虑，星点质心位置精度包含如下几个要素：

1) 基准恒星自身的质心位置精度

通常根据星相机星等探测能力分析确定基准恒星类型，光学系统设计时主要以基准恒星光谱作为设计输入，考虑到其星点质心位置与光斑形状有关，为便于质心提取，设计过程中需使光学系统的弥散斑形状尽量接近圆形，而光斑形状与光学系统的非对称像差相关，因此，对于星相机设计过程中需考虑倍率色差；此外，畸变的存在同样影响轴外星点在像面上的成像位置，设计过程中亦需考虑.

2) 其他恒星与基准恒星的位置精度

其他恒星与基准恒星间的质心位置差异本质是不同类别恒星间色温不同导致的波长权重的区别，推演到像差本质主要还是倍率色差的影响，此时畸变亦同样存在.

3) 星点质心位置精度和质心位置与理想像点位置之间关系

理想像点通常为高斯像点，其在高斯像面上的垂轴高度就是理想像高[17].一般星相机内方位元素标定过程中是以靶标点质心位置代替实际像高，通过其与理想像高之间的偏差最小二乘进行数据拟合，此过程中只近似考虑了主光线的畸变像差，未考虑质心位置畸变的影响，如不对该指标进行评价，对星相机而言其光学系统性能将不能准确标定.

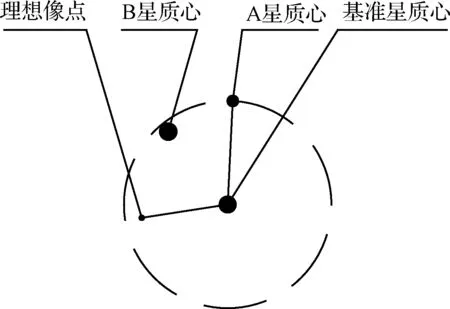
图1　星点质心位置分解示意图Fig.1　Schematic diagram of the star’s centroid position decomposition

1.2　星相机光学系统性能评价方法

传统的像质评价方法只有5种，分别是适用于小像差光学系统的Reyleigh判断、中心点亮度，适用于大像差光学系统的分辨率、点列图及两种光学系统均适用的光学传递函数[18].其中前4种评价方法是以点源目标成像时的能量集中程度来表征光学系统的成像质量的.在不考虑衍射的情况下，光学系统的成像质量主要与系统的像差大小有关，而像差理论是光学设计的理论基础.考虑衍射现象时，可以通过实际成像波面或光学传递函数评价.所以，星相机光学系统设计阶段需通过光学传递函数曲线、能量集中度曲线、色温及温度变化(均匀温升和温度梯度变化)情况下星点质心位置精度、质心位置与理想像高的偏差、光学系统像差(倍率色差、畸变)来评价星相机光学系统.当然，这使星相机光学系统的设计提升到了前所未有的难度.

基于上述评价指标，光学系统设计之初先综合权衡光学系统的MTF，同时考虑要求像元内的能量集中度，当规定像元对应的频率处光学系统传递函数达到一定程度时，对光学系统的倍率色差和畸变进行校正，当畸变和倍率色差校正到技术指标要求范围内时，可以认为基准恒星质心位置已经确定.当基准恒星质心位置相对固定后再考虑其与高斯像点之间的偏差.其他恒星相对于基准恒星的质心位置偏差此时也不会很大，可进行适当校正.最后基于初始结构确定前的消热差理论综合考虑消热特性[19-20].

2　光学系统设计实例

根据上述光学系统设计评价方法及思路，在给定光学系统设计指标的前提下进行星相机光学系统设计，最后对光学系统成像质量通过各类曲线及质心位置精度进行了评价.

2.1　设计指标

设计指标如表1所示.

表1　光学系统设计指标Tab.1　Parameters of optical design

2.2　设计结果及像质评价

根据设计指标要求，选取有利于校正轴外像差的对称式双高斯系统为初始结构，并进行复杂化.设计过程中结合消热差理论主要保证光学系统弥散斑形状，当光学系统MTF接近衍射极限后，对光学系统的非对称像差及畸变进行控制，最终得到一个八片球面镜有利于工程实现的光学系统.设计结果如表2所示.

光学系统结构形式如图2所示.

表2　光学系统设计结果Tab.2　Results of optical system design

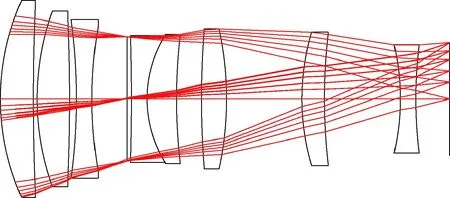
图2　光学系统结构示意图Fig.2　Schematic diagram of the optical system

光学系统场区及畸变曲线如图3所示.中心设计波长畸变小于等于0.5 μm，最大畸变小于1.8 μm.倍率色差曲线如图4所示，倍率色差小于0.8 μm.能量集中度曲线如图5所示，3×3像元内能量集中度均值>90%.点列图如图6所示，除边缘视场外系统点列图基本接近圆形.

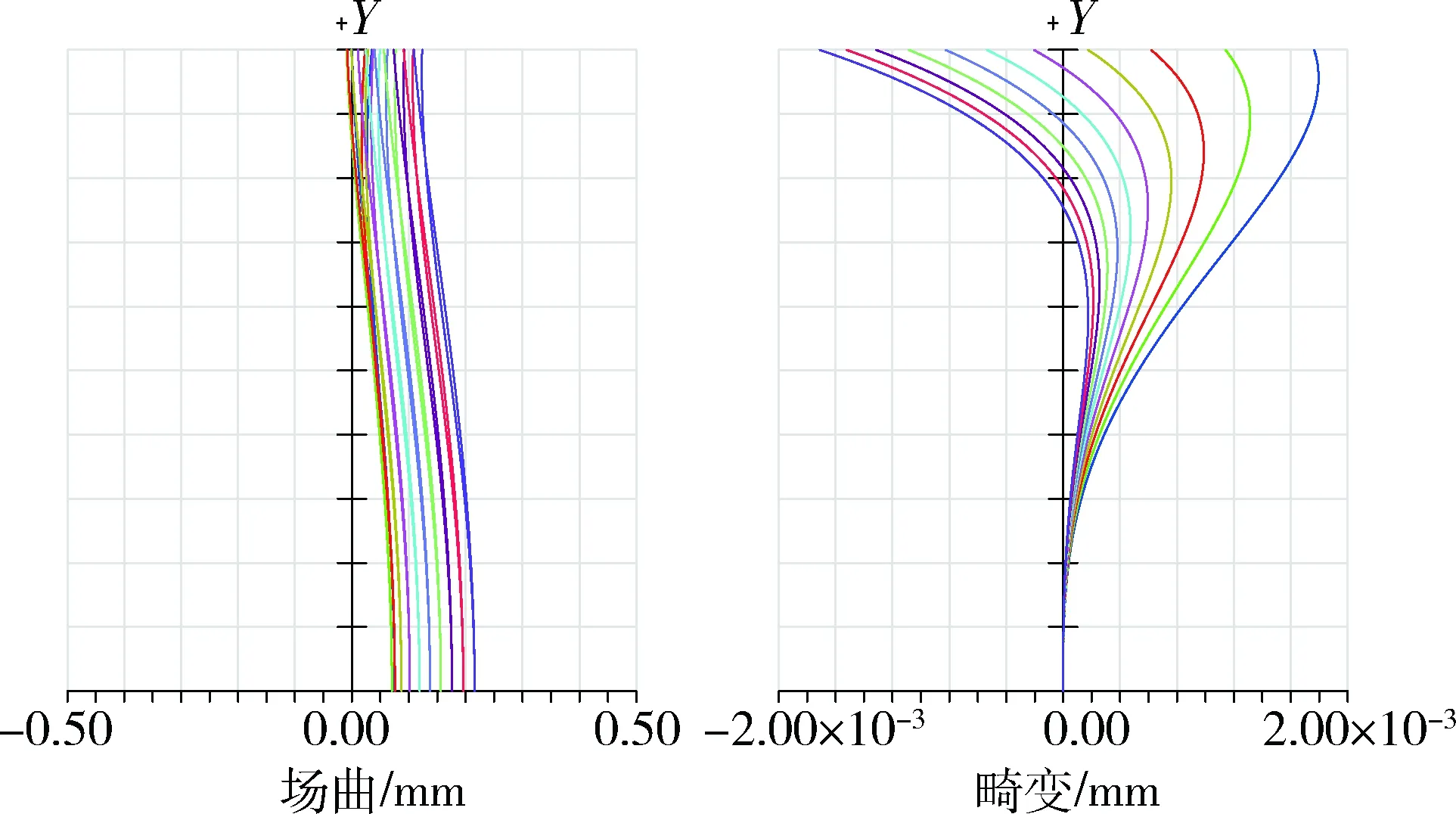
图3　光学系统场曲畸变曲线Fig.3　Field curve/distortion of the optical system

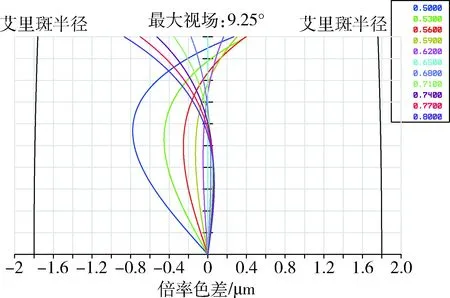
图4　光学系统倍率色差曲线Fig.4　Lateral color of the optical system

2.3　质心位置精度分析

2.3.1其他恒星与基准恒星间的质心位置偏差

根据目标星等在天区中的分布情况，选取K类恒星为基准，计算其他各类恒星的质心位置相对于基准恒心的质心位置偏差如表3所示，全视场范围内恒星色温变化导致的质心位置偏差最大值为0.33 μm，对于大视场星相机光学系统而言，该值很小.

2.3.2质心位置与理想像高偏差

各种类别恒星质心位置相对于中心设计波长光线理想像高的偏差如表4所示，全视场范围内恒星色温变化导致的质心位置与理想像高的最大偏差为0.65 μm.

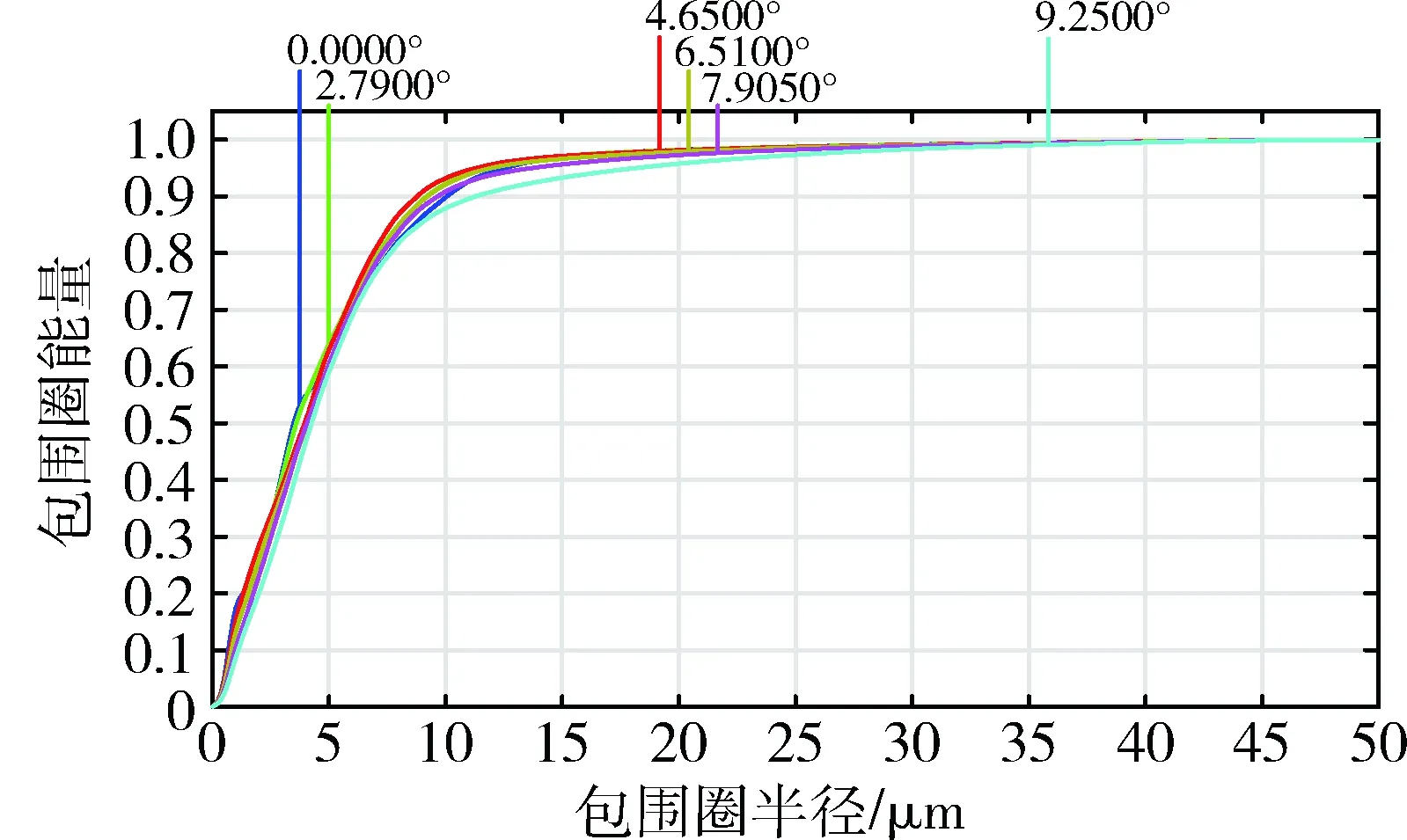
图5　光学系统能量集中度曲线Fig.5　Encircled energy of the optical system

图6　光学系统点列图Fig.6　Spot diagram of the optical system

表3　各类恒星与基准恒星的质心偏差Tab.3　Centroid deviation of distinguished and fixed star

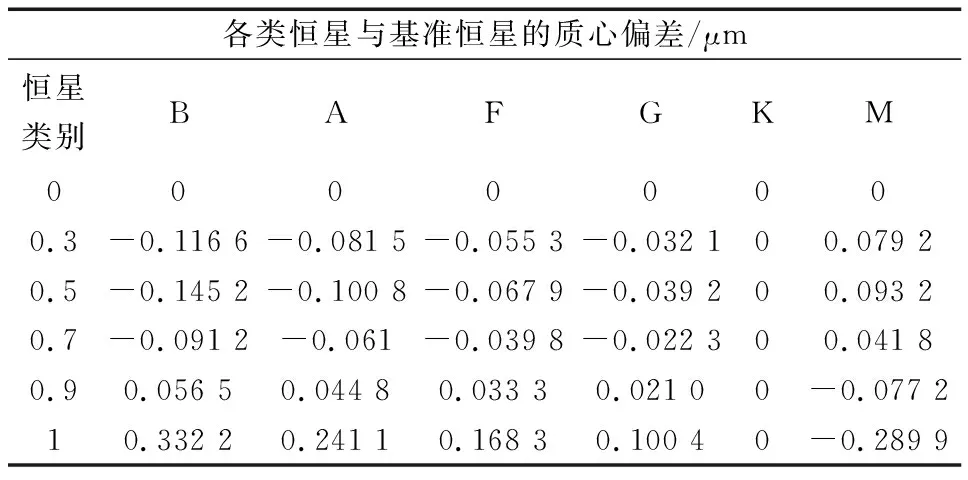
各类恒星与基准恒星的质心偏差/μm恒星类别BAFGKM00000000.3-0.116 6-0.081 5-0.055 3-0.032 100.079 20.5-0.145 2-0.100 8-0.067 9-0.039 200.093 20.7-0.091 2-0.061-0.039 8-0.022 300.041 80.90.056 50.044 80.033 30.021 00-0.077 210.332 20.241 10.168 30.100 40-0.289 9

2.4　温度稳定性分析

温度稳定性分析过程以光学系统第一片透镜位置作为固定端，焦面位置根据实际温变情况自由膨胀.光学系统结构件采用铝合金(线胀系数为23.1×10-6/K)材料，计算15 ℃、20 ℃、25 ℃ 3个温度条件下光学系统的质心位置偏差及质心位置与理想像高的偏差.分析结果表明光学系统焦距变化量小于等于4.5 μm.

2.4.1均匀温度分析

以20 ℃条件下基准恒星质心位置为基准，评价温度改变后，光学系统各类恒星质心位置与基准位置之间的偏差如表5、6所示.15 ℃条件下，全视场范围内各类恒星与20 ℃基准恒星的质心位置偏差最大值为0.32 μm；25 ℃条件下，全视场范围内各类恒星与20 ℃基准恒星的质心位置偏差最大值为0.36 μm.可见，温度变化情况下各类恒星与基准恒星间的质心位置偏差较小.

以20 ℃条件下理想像高为基准，评价温度改变后，光学系统各类恒星质心位置与中心设计波长理想像高之间的偏差如表7、8所示.15 ℃条件下，全视场范围内各类恒星与20 ℃理想像高偏差最大值为0.66 μm；25 ℃条件下，全视场范围内各类恒星与20 ℃理想像高偏差最大值为0.64 μm.可见温度变化情况下，质心位置畸变变化不大.

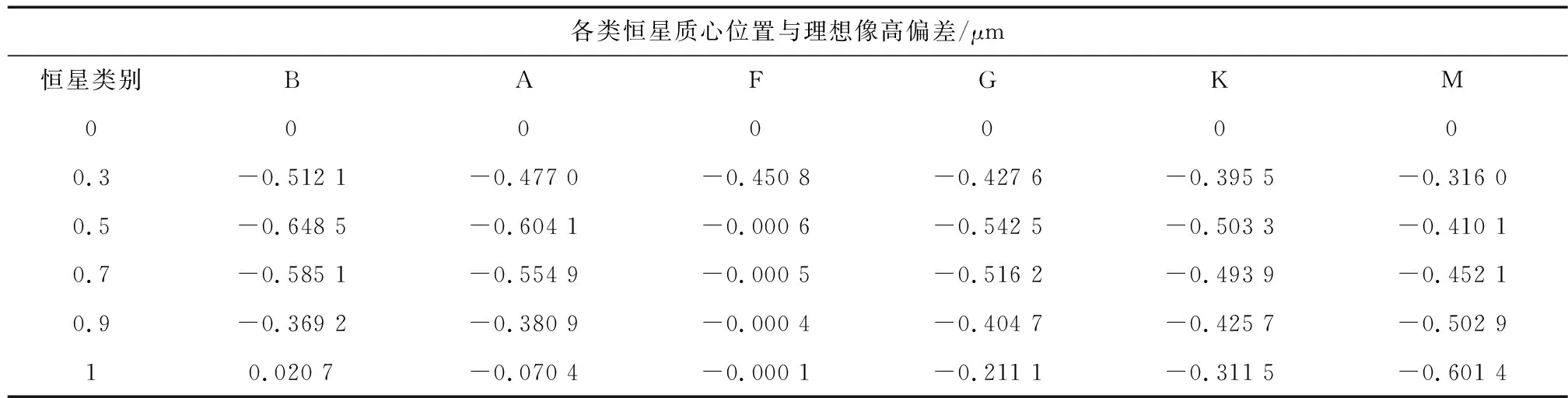
表4　各类恒星质心位置与理想像高的偏差Tab.4　Deviation of centroid position of distinguished star and ideal image height

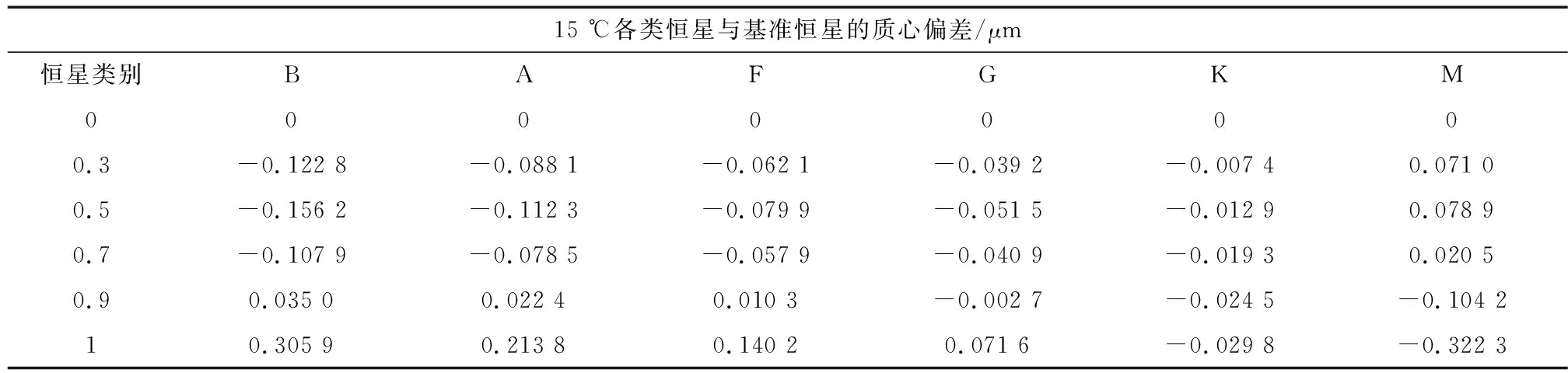
表5　15 ℃各类恒星与基准恒星的质心偏差Tab.5　Centroid deviation of distinguished and fixed star at 15 ℃

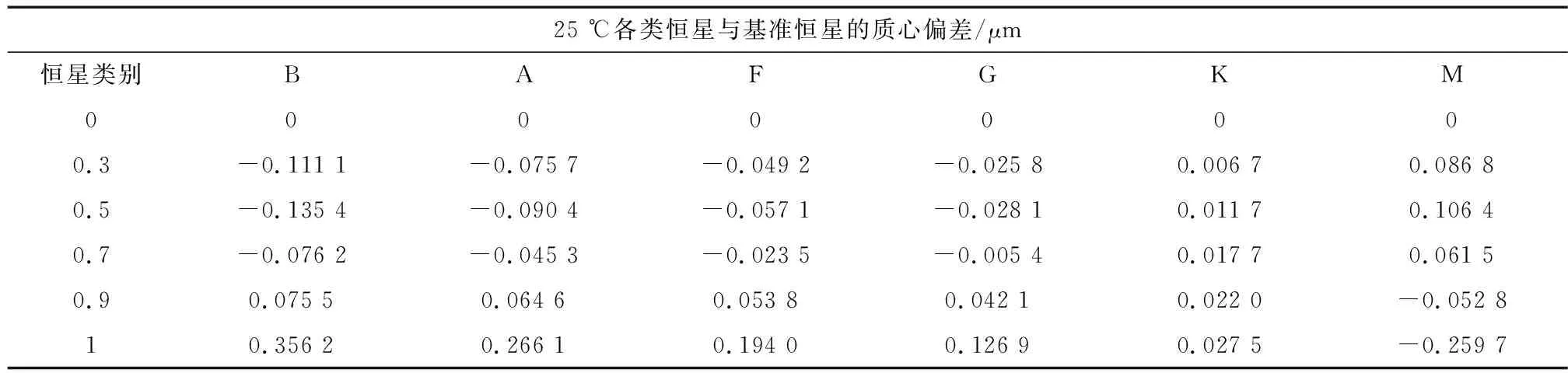
表6　25 ℃各类恒星与基准恒星的质心偏差Tab.6　Centroid deviation of distinguished and fixed star at 25 ℃

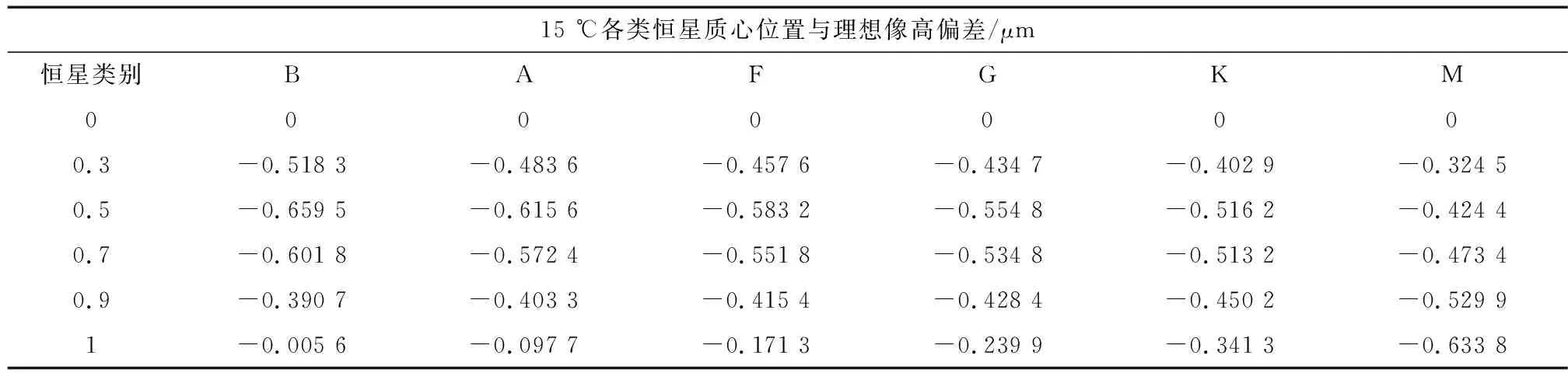
表7　15 ℃各类恒星质心位置与理想像高偏差Tab.7　Deviation of centroid position of distinguished star and ideal image height at 15 ℃

表8　25 ℃各类恒星质心位置与理想像高偏差Tab.8　Deviation of centroid position of distinguished star and ideal image height at 25 ℃

2.4.2梯度温度分析

以20 ℃条件下基准恒星质心位置为基准，评价温度改变后，光学系统各类恒星质心位置与基准位置之间的偏差如表9所示.其中梯度温度指沿光学系统径向存在的温度梯度差异.0.5 ℃梯度温度条件下，全视场范围内各类恒星与20 ℃基准恒星的质心位置偏差最大值为0.34 μm.可见，梯度温度变化情况下各类恒星与基准恒星间的质心位置偏差较小.

以20 ℃条件下理想像高为基准，评价温度改变后，光学系统各类恒星质心位置与中心设计波长理想像高之间的偏差如表10所示.0.5 ℃梯度温度条件下，全视场范围内各类恒星与20 ℃理想像高偏差最大值为0.65 μm.可见温度变化情况下，质心位置畸变变化不大.

表10　0.5 ℃温度梯度各类恒星质心位置与理想像高偏差Tab.10　Deviation of centroid position of distinguished star and ideal image height at 0.5 ℃ gradient

2.5　设计小结

3　结　论

针对高精度星相机光学系统的实际使用需求，对影响其性能的星点质心位置指标进行了系统分析，阐述了星相机光学系统设计过程中分析质心位置与理想像高间的偏差、不同温变条件下各类恒星相对于基准恒星质心位置的稳定性的必要性，并以大视场无热化星相机光学系统设计为例，按照相应的评价指标分析了其质心位置精度及温度稳定性，为高精度星相机光学系统设计提供了有益参考.