含有多级驱动机构卫星的多变量频域稳定性分析方法*

刘　磊

0　引　言

当前空间激光通信、天文观测以及极高分辨率对地观测等未来先进航天器对指向控制的精度、稳定度都提出了更高的需求[1-3].一方面，星上帆板、控制力矩陀螺等扰动源产生的低频振动和高频抖动会严重影响指向精度和稳定度.另一方面，敏捷卫星对任务的快速响应要求机动后载荷指向快速稳定.因此，卫星控制正在探索由平台控制和含有多级机构的复合控制，来实现精确指向、扰振补偿和振动隔离.运用多级复合控制方法，解决航天器控制中的“准、稳、快”的突出矛盾问题.

近年来，COBB等[4-5]采用多级驱动机构实现了精密有效载荷的主动指向调节与振动隔离.VALLONE等[6]针对未来空间天文观测ACCESS任务，研制并验证了多级驱动机构的精确指向和主动隔振能力.CHEN等[7]通过试验对比多级驱动机构不同控制方法的优缺点.MCINROY等[8]研究了容错、精确指向鲁棒控制方法，并给出了系统化的分析流程.以上研究从多级驱动机构的设计、研制、建模、控制方法等方面取得很大进展，但对一体化模型的稳定性分析研究涉及甚少.

含有多级驱动机构卫星在多自由度控制器增加的同时也引入了星体和载荷之间的多回路耦合，是典型的多输入多输出耦合的系统，给系统稳定性分析带来较大困难.此外，虽然理论建模通常采用时域方法得到状态空间描述的一体化模型，但实际应用模型的结构模态特性多以频域方法分析.因此有必要针对一体化模型，采用物理意义的多变量频域方法进行稳定性分析研究.

基于上述研究现状和存在问题,本文提出一种针对含有多级驱动机构卫星多级复合控制系统的多变量频域稳定性分析方法.首先，建立含有多级驱动机构卫星一体化线性模型，设计线性反馈控制器.在此基础上，利用多项式矩阵变换得到多通道闭环系统极点分布规律，确定闭环系统多变量频域输入输出稳定性条件.最后，针对方法的正确性和有效性进行了算例和模型仿真验证.

1　含有多级驱动机构卫星一体化建模

1.1　运动学模型

如图1所示的含有多级驱动机构卫星，由星体、挠性附件、多级驱动机构和载荷组成.

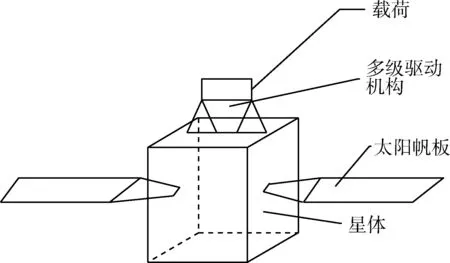
图1　含有多级驱动机构卫星示意图Fig.1　Schematic diagram of satellites with multi-stage drive mechanism

图2给出了一般构型的多级驱动机构平台坐标系示意图.定义各坐标系如下：

整星坐标系(o-xyz，简称O系)：坐标原点o固定于整星质心，坐标轴平行于卫星本体坐标系.

卫星本体坐标系(ob-xbybzb，简称B系)：固定在卫星本体上，坐标系原点ob为卫星本体质心，obxb指向卫星飞行方向，obzb指向地心，obyb与obxb和obzb构成右手直角坐标系.

载荷坐标系(op-xpypzp，简称P系)：固定在载荷上，坐标系原点op为载荷质心，三轴方向定义同卫星本体坐标系.

轨道坐标系(oor-xoryorzor，简称Oor系)：xor轴指向轨道运动前方，zor轴方向指向地心.

针对如图2所示的多级驱动机构的一般构型，运动学关系可表示为

(1)

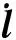
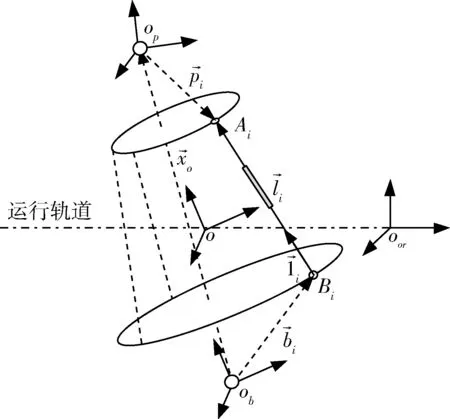
图2　一般构型的多级驱动机构坐标系示意图Fig.2　Schematic diagram of a multi-stage drive mechanism in general configuration

因此，在位移量很小的条件下

(2)

由虚功原理可得力/力矩传递关系为

(3)

其中，Fl,Plp,Tlp,Plb,Tlb分别为驱动输出力、驱动器对载荷的合力、驱动器对载荷的合力矩、驱动器对星体的合力、驱动器对星体的合力矩.

1.2　动力学模型

动力学建模考虑载荷、星体以及挠性附件的整体动力学模型.由Newton-Euler法得到动力学方程并写成状态空间表达式.由于平台相对位移较小，状态方程形式对动力学方程进行了简化(如忽略了二阶小量、状态变量近似等).首先对单自由度驱动器的动力学模型进行建模.

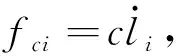
(4)

根据式(4)可得驱动机构的输出力向量可表示为

(5)

式中，Fl,Fa,Fk,Fc分别表示输出力、控制力、弹性力、阻尼力向量，K,C分别表示刚度矩阵和阻尼矩阵.

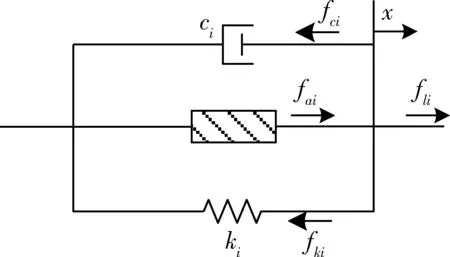
图3　单自由度驱动器的动力学模型Fig.3　Dynamic model of single degree of freedom actuator

首先将载荷视为刚体，在o-xyz坐标系中，载荷动力学方程为

(6)

将星体视为刚体，其受到的外力/力矩包括驱动机构的作用力/力矩、直接作用在载荷上的控制力/力矩和直接作用在载荷上的扰动力/力矩.在o-xyz坐标系中，星体动力学方程为

(7)

以上是将载荷和星体等效为纯刚体模型，考虑挠性附件影响，采用混合坐标法建立包含挠性附件的整个航天器系统有限自由度的动力学模型.

考虑载荷和星体上的挠性附件，根据混合坐标法可知，载荷动力学方程可写为

(8)

星体动力学方程可写为

(9)

式中，m,n分别为载荷和星体上挠性附件个数，ηpi,ηbj分别为载荷和星体上第i个挠性附件的M、N维模态坐标，M、N为模态阶数，Ptrani,Btranj分别为载荷和星体的平动耦合系数矩阵，Proti,Brotj分别为载荷和星体的转动耦合系数矩阵，ξpi,ξbj分别为载荷和星体的结构阻尼系数矩阵，Ωpi,Ωbj分别为载荷和星体的模态频率对角矩阵.

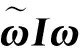
Xp=[xp,yp,zp,θxp,θyp,θzp]T,

Xb=[xb,yb,zb,θxb,θyb,θzb]T,

(10)

其中，状态变量x为

(11)

状态矩阵A,B,C,D分别表示为

Ψ2=

输出变量表示为

(12)

输入变量表示为

u=[udpudb+ucFa]T

(13)

式中,udp,udb分别为作用在载荷和星体上的扰动力/力矩，uc作用在星体上的控制力/力矩列阵，Fa为驱动器的控制力.需要注意的是，载荷控制器的输出量为载荷的控制力矩，因此将式(10)中的输入矩阵改写为

(14)

系统输入变为

(15)

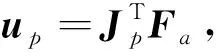
2　单通道控制器设计

通过动力学建模可知，含有多级驱动机构卫星多级姿态控制系统对象是多输入多输出系统.针对多输入多输出系统首先应考虑解耦控制，由多输入多输出系统解耦条件可知，输入输出维数相同是能够通过输入变换和状态反馈矩阵进行解耦的必要条件，因此系统无法实现动态或静态解耦.

为便于控制器设计，在控制器设计时将系统简化为多个单通道的单输入单输出系统，即只考虑一个输入与一个输出之间的传递函数.

针对式(10)所示的线性时不变系统的第i个输入ui至第j个输出yj的传递函数为Gji(s),则系统的传递函数G(s)可写为

(16)

式中，b为输入变量维数，a为输出变量维数.

考虑载荷控制力矩到载荷姿态，星体控制力矩到星体姿态之间的传递函数，只针对六路单通道输入输出系统进行控制器设计.例如，对于载荷x轴姿态yx(s)与x轴转矩ux(s)的单通道系统的传递函数为Gxx(s).需要注意的是，这里的单通道系统仅表示单输入和单输出之间的传递函数，实际的x轴姿态输出为多个输入作用的叠加，只不过这里ux(s)Gxx(s)为yx(s)的主要部分.

针对单通道系统Gji(s),可以采用PID控制器进行控制.由于控制器设计基于简化控制器设计和小位移内不同变量之间耦合较小的假设，将含有多级驱动机构的多输入多输出系统简化为单输入单输出系统.此外，这里只讨论了载荷姿态的控制器设计方法，对于星体一级控制，可采用传统的卫星姿态控制方法设计控制器.

3　多变量频域稳定性分析方法

上述控制器设计方法是基于耦合量较小的实际工况和简化控制器的应用需求对多输入输出系统简化，并对载荷和星体分别设计控制器的方法.该方法能方便地对控制器参数进行设计，并直接得到单输入单输出通道的稳定性分析结果.但是由一体化建模和控制器设计过程可知，各通道之间存在耦合且控制器包含多个回路，单输入单输出系统稳定的结论并不能从理论上保证多输入输出系统的稳定性.本小节将采用多变量频域稳定性分析方法，对以上存在耦合多回路的含有多级驱动机构卫星多级姿态控制系统进行稳定性分析.

首先，线性系统的稳定性可分类为基于状态空间描述的内稳定性和基于输入输出描述的外稳定性.对于n维连续时间线性时不变系统(16)，稳定性分析基于以下定理：

定理1[9].外稳定即输入输出稳定(BIBO)的充分必要条件为真或严真传递函数G(s)所有极点均为负实部.

以上控制器可等价为单通道线性反馈回路，如图4所示.因此考虑任意单通道线性反馈回路对系统稳定性的影响.由式(16)得开环系统可表示为

(17)

设单通道线性反馈后的输入为

(18)

将式(18)带入式(17)并作行列变换可得

(19)

从式(19)可以看出系统增加了一路单通道输出线性反馈，即

(20)

对式(20)进行化简得

(21)

则输入输出可描述为

(22)

图4　单通道线性反馈系统框图Fig.4　Single-channel linear feedback systemblock diagram

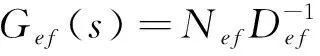
(23)

其中ρefgh(s)=φ/(DefDgh)为φ除以DefDgh的余数多项式.因此，G(s)中任意两个不同行且不同列的元传递函数的乘积，分母为特征多项式φ(s).进而，式(22)元传递函数分子中包含线性反馈的因式可表示为

(24)

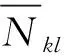
(25)

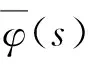
定理2.若多输入多输出开环系统是BIBO的，引入一路单通道输出线性反馈且该单通道闭环系统是BIBO的，则得到的多输入多输出闭环系统也是BIBO的，且系统闭环极点满足式(25)所示的特征多项式.

因此，含有多级驱动机构卫星可通过对控制回路中的所有单通道进行逐次稳定性设计，最终得到的多级姿态控制器可以保证多输入多输出闭环系统的稳定性.相比状态空间法，该多变量频域方法具有物理直观性强、便于控制器设计和调整的特点.

4　仿真分析

4.1　简化算例验证

取传递函数矩阵输入输出描述的系统如式(26)所示，系统输入维数为3，输出维数为2

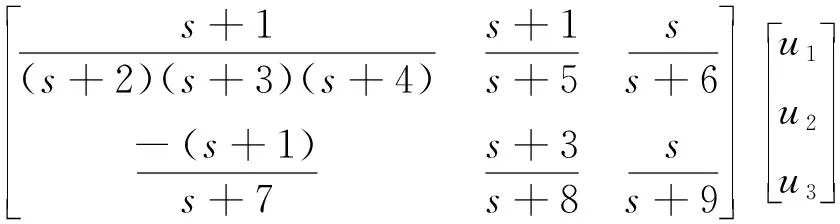
(26)

在输入u1到输出y1之间的单通道中引入输出线性反馈H11(s),令H11(s)=(s+10)-1,则有

(27)

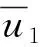
(28)

其中由式(26)得，式(28)中D11=(s+2)(s+3)(s+4),DH11=(s+10),N11=(s+1),NH11=1.

因此可得系统特征多项式为

(29)

其中，ρ11(s)=(s+5)(s+6)(s+7)(s+8)(s+9),即开环系统其余通道的极点多项式.通过图5中极点分布可知，相比开环系统，该通道输出线性反馈后的系统闭环极点保留了开环系统其余通道的极点(-5，-6，-7，-8，-9)，其余为该通道闭环系统极点(-1.946，-3.0354±0.5091i，-10.03).

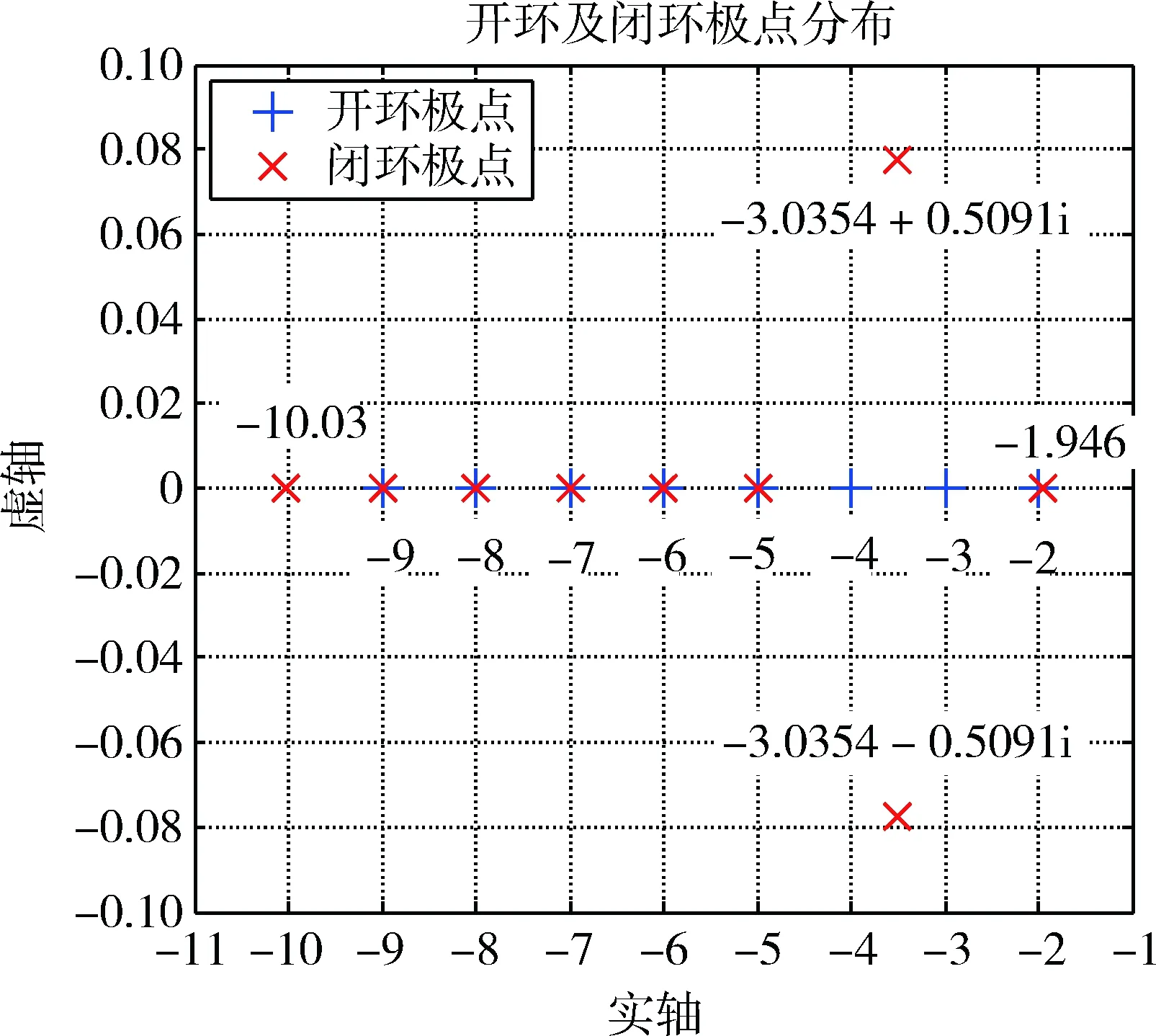
图5　算例开环及闭环极点分布图Fig.5　Open-loop and closed-loop polar distributions of the examples

4.2　含有多级驱动机构卫星模型仿真

采用式(10)得到的含有多级驱动机构卫星模型进行仿真验证.模型参数如表1所示.

表1　含有多级驱动机构卫星模型仿真参数Tab.1　Simulation parameters of satellites with multi-stage drive mechanism

为简化分析首先采用纯刚体模型，得到开环系统极点分布如图6所示，开环系统极点均在左半平面或原点处.该极点分布表明开环系统是BIBO的.

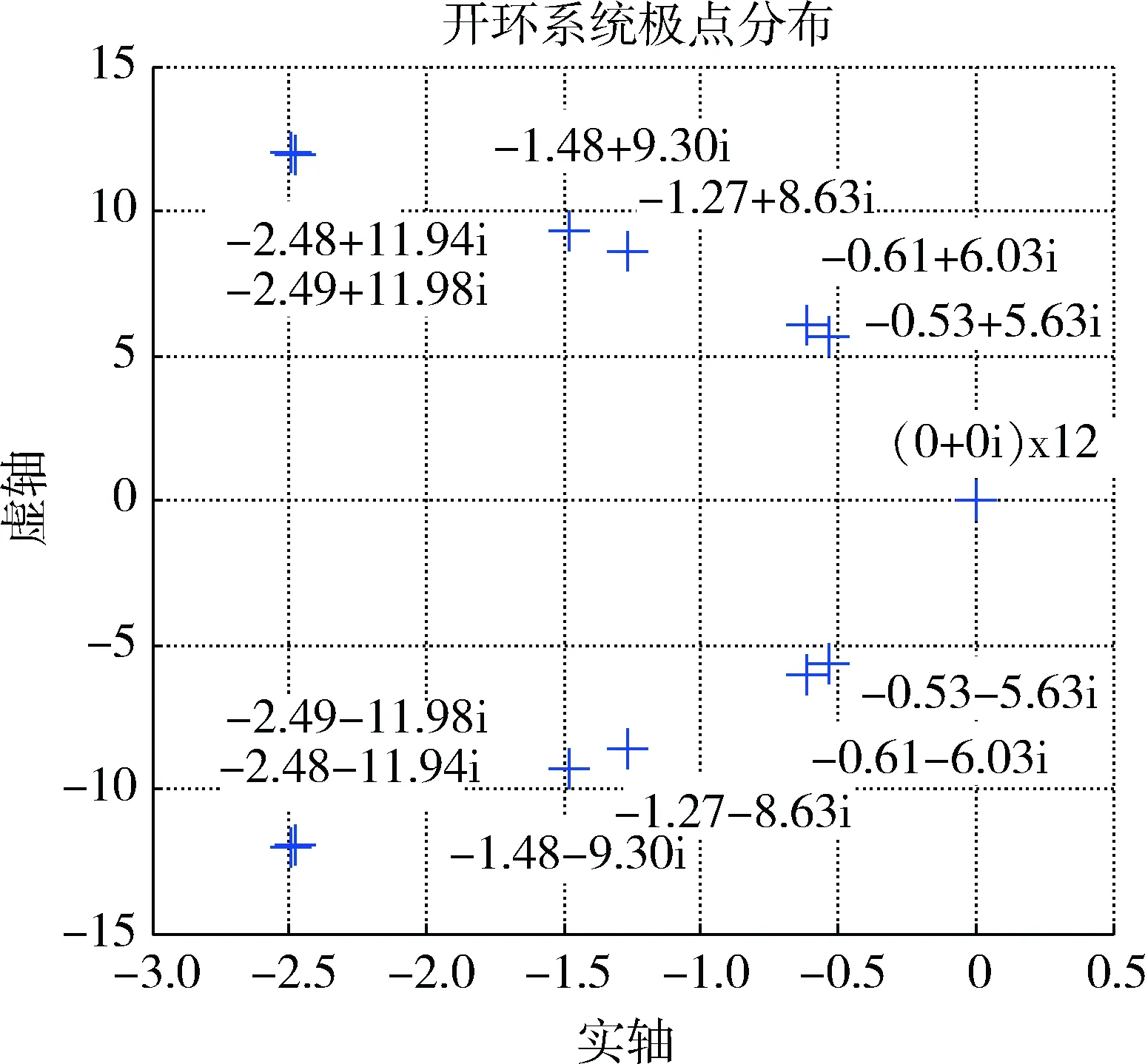
图6　开环系统极点分布图Fig.6　Polar distribution of open-loop system

对单个驱动器进行闭环控制，得到系统极点分布与开环极点分布比较，如图7所示，其中上图表示仅对1个驱动器进行闭环后的极点分布.驱动器闭环即在驱动器单通道增加了输出线性反馈，取该线性反馈的传递函数为314 169.0(s+31.4)-1.从图7中可看出，每个通道的闭环会增加一个极点，且由于该通道开环极点不包括非零极点(即整星转动和平动模态)，因此驱动器闭环后保留了为零极点，仅使非零极点向左移动.

在驱动器闭环的基础上，按照表1中星体和多级驱动机构的控制参数进行控制器设计，得到星体和载荷控制闭环后的极点分布如图8所示.以星体单轴通道比例-微分控制器为例，控制器传递函数为NHij=1 035s+464.6,DHij=1.由式(25)可知，由于该通道传递函数具有严真性即degDji>degNji,因此极点个数没有增加.多级驱动机构控制器传递函数为NHij=s2+10s+42.5,DHij=0.000 125s.从图8中可以看出，在负实轴上增加了两个稳定的极点.

图7　驱动器闭环与开环系统极点分布Fig.7　Pole distribution of open-loop system and drive closed-loopsystem

图8　闭环系统与开环系统极点分布图Fig.8　Pole distribution of open-loop system and closed-loop system

为进一步验证星上挠性附件对稳定性的影响，将包含挠性附件的模型进行仿真，得到如图9所示的包含挠性附件极点的极点分布图.由于挠性附件模态频率较高、极点的阻尼比较小，因此与刚体模型得到的开闭极点距离较远，针对中心刚体模型设计的反馈通道对挠性附件极点的改变很小，可近似解耦.然而，当挠性附件模态分布与包含多级驱动机构的刚体模型模态分布近似时，控制器设计需要同时考虑挠性附件对稳定性带来的影响.

以上针对简化算例和实际模型的仿真分析，验证了式(25)给出的多输入多输出开环系统极点与输出反馈闭环系统极点的分布关系.因此，该方法可作为含有多级驱动机构卫星闭环系统稳定性的验证依据，也为控制器参数稳定性分析提供了简单有效的工具.

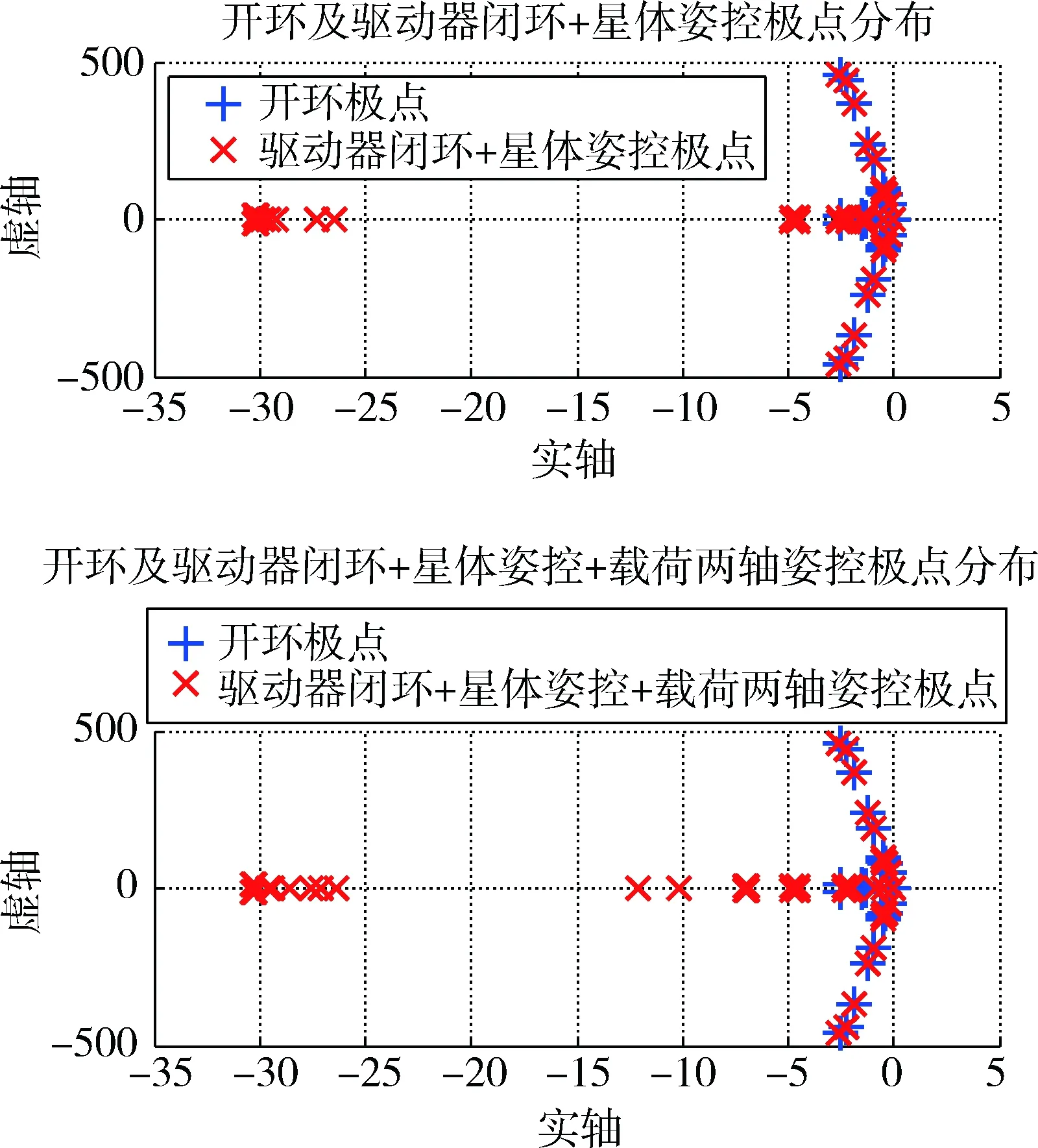
图9　包含挠性附件系统极点分布图Fig.9　Pole distribution with flexible accessories system

5　结　论

针对含有多级驱动机构卫星多级复合控制系统稳定性分析问题，本文提出了一种多变量频域分析方法.建立了含有多级驱动机构卫星一体化线性模型，针对星体和载荷姿态设计了单通道输出线性反馈控制器.对传递函数矩阵变换，得到多通道闭环系统极点分布规律，为含有多级驱动机构卫星闭环系统稳定性分析和参数设计提供了有效工具.

本文提出的针对多输入多输出系统的多变量频域稳定性分析方法可进一步推广应用于其它多输入多输出线性系统的稳定性分析问题中.