再入飞行器末端能量管理段纵向剖面优化方法*
2018-07-12龚宇莲陈上上
龚宇莲,陈上上
0 引 言
可重复使用的轨道再入飞行器是近年来国内外航天航空领域的研究热点之一.以航天飞机为代表的轨道再入飞行器,其再入返回一般包括初期再入段、末端能量管理段(terminal area energy management, TAEM)以及进场着陆段.末端能量管理段是初期再入段与自动着陆段之间的过渡,这一阶段的飞行任务是消除初期再入段结束时飞行状态的大范围散布,利用该飞行阶段的机动能力,将飞行状态调整到满足进场着陆起点的精度要求.末端能量管理段GNC系统的任务是规划并跟踪一条合理的轨迹,将飞行器的飞行高度从距机场水平面约30 km降到约3 km,速度从约2.5 Ma降到满足着陆起点的要求,并且使飞行器航向对准机场跑道,航迹倾角,横侧向位置满足自动着陆要求[1].
对于飞行器末端能量管理段的研究,主要集中在轨迹规划与制导律设计问题.以航天飞机为基础的制导策略,是基于标称条件下的设计,其核心是离线设计的能量-航程剖面.文献[1]详细描述了航天飞机TAEM段制导控制方案及其历史发展.航天飞机采用了标称轨迹法,根据不同状态预先设计了不同的标称能量和标称高度剖面.航天飞机多次飞行的成功也证明了该方法具有很强的鲁棒性.除标称轨迹方面的研究外,在线生成轨迹以及自适应轨迹生成方法方面近年来也有大量学者研究.文献[2~5]中,采用了不同的方式通过在线递推,确定地面轨迹.文献[2]的地面轨迹利用可调整参数的螺旋线,通过在线确定螺旋线的3个参数确定最终的轨迹.文献[3]中初期以固定的倾侧角飞行,中途修正一次倾侧角符号,从而调整航向使之对准航向校准圆(heading alignment cylinder,HAC)切线,作者通过在线反复迭代计算获得最优的倾侧角翻转时间以及HAC位置.文献[4]中通过在线确定3个圆弧的几何位置,使得地面轨迹满足预先计算的航程要求.文献[5]则是在线确定HAC圆的位置选择合适的航程.文献[6~8]中则考虑为飞行器设计一个合适的高度动压剖面,对飞行器纵向轨迹进行优化.对于无动力轨道再入飞行器,其飞行能力很大程度受制于飞行器的自身气动特性.对于飞行器轨迹优化的方法有很多,但不管哪种方法,都需要知道飞行器的能力限制以及最优的纵向轨迹策略.文献[9~10]提出energy-tube的概念,能量截面包含了可达到一定航程的高度和速度的组合,并在此基础上研究最优的HAC圆策略,但其并未严格约束TAEM末端点的状态量.本文对飞行器的纵向轨迹优化问题进行研究,算法中对飞行器TAEM段初末状态都进行了严格的约束.
本文首先给出了单条TAEM段纵向轨迹数值递推及调整方案,而后提出了一种TAEM段航程的优选方法,以阻力板控制裕度最大为优化目标,优选出最适合飞行器升阻特性的航程以及相应的高度动压剖面.最后通过考虑初期状态散布以及气动不确定性情况下的六自由度动力学打靶仿真,对通过优选确定的纵向轨迹的鲁棒性进行验证.
1 可行轨迹分析
忽略地球自转的无动力飞行器纵向动力学方程可以表达为[2]:
(1)
式中:h,V,γ,s分别为飞行器的高度,速度,爬升角以及待飞距.r为地心距,g为引力加速度,φ为飞行器的倾侧角.L和D分别为升力加速度和阻力加速度,L=qSrefCL/m,D=qSrefCD/m.其中CL,CD为升力系数与阻力系数,q=0.5ρV2为动压,Sref为飞行器参考面积,m为飞行器质量.
对于无动力轨道再入飞行器,其航程能力受限于飞行器的升阻特性.因此,这类飞行器轨迹设计的首要问题是明确飞行器的航程能力.在准平衡滑翔等近似条件下可以推导出飞行器按最大升阻比飞行时达到最长航程.因此,在TAEM段轨迹设计中,研究者一般使飞行器攻角保持在最大升阻比条件下开环仿真,得到最长航程.但采用最大升阻比飞行所确定的最长航程,其末端点一般不能满足飞行器着陆起点的高度速度需求.因此最大升阻比航程仅能反映飞行器的极限飞行能力,而不能反映完成TAEM段任务需求的航程能力.飞行器的最短航程通过最陡下降弹道获得,最陡下降弹道由飞行器的动压及过载约束决定.开环仿真中,令飞行器沿最大动压剖面飞行,可获得最短航程.实际操作中,由于动压的变化与高度和速度变化密切相关,受升力与阻力综合作用,跟踪一条动压剖面可选择的控制量的自由度较大.如通过调整攻角改变升阻比实现动压的跟踪,或调节阻力板改变阻力实现动压跟踪,也可以通过变化倾侧角改变升力方向实现动压跟踪.不同的动压跟踪方法将产生不同的航程长度,因此,仅考虑动压跟踪所得到的航程并不惟一.
对于类似航天飞机的轨道再入飞行器,其末端能量管理段的终点对飞行器的动压、高度、高度下降率均有要求.满足飞行任务的剖面需考虑的条件如下:
(1) 初末状态的高度、速度、航迹倾角满足设计要求.TAEM段剖面设计时,将初期再入段末端点作为状态初值,末端点状态则由自动着陆需求给出:
初始状态:V0=VE,h0=hE,γ0=γE;
末端状态:qend=qf,hend=hf,γend=γf;
其中VE,hE,γE,qf,hf,γf为确定值.
(2) 飞行过程不超过最大动压及最大过载限制.飞行器的动压和过载约束由结构强度所决定.由于侧向过载在保持侧滑角为零时通常较小,所以设计中只需考虑法向过载nz.因此在整个飞行剖面内需要满足q (3) 飞行轨迹是物理可实现的.这项约束是指飞行轨迹需满足公式(1)所示的状态方程. 任何一条弹道如果满足上述3个条件,即可以认为是满足TAEM段任务需求的弹道.可见,飞行器的纵向剖面不需要始终沿着一条标称的动压剖面飞行,只需在末端点达到需要的动压.同样,飞行器也不需要始终沿着规划的参考高度剖面飞行,只需在末端点达到需要的高度以及高度下降率.因此本文的轨迹生成以满足TAEM初末状态和飞行器动压限制为目标进行纵向递推,并优选出不同航程对应的纵向参考轨迹,从而给出一种鲁棒性最强的TAEM段标称航程,为初期再入段的末端点的选取提供依据. 本文最核心的问题是期望确定出一个无动力飞行器末端能量管理段飞行的最优航程以及对应的最优动压剖面.为实现航程优化,本文对各种航程进行遍历递推,而后通过指标优选出鲁棒性最强的航程.为实现单条轨迹的推衍,确定好待飞航程后首先确定一条参考高度-动压剖面以及一条高度-航程曲线,并在递推过程中根据飞行器实际的升力阻力限制对预置的剖面进行动态调整. 类似于航天飞机采用的三次曲线[5]本文采用如式(2)所示的分段二次曲线作为参考高度曲线. (2) 假定初始的待飞距为s0,Sm∈(0,s0)为两段二次曲线的分段点,sm是一个可调参数.根据已知的初末高度以及初末爬升角,以及设定的待飞距s0可以确定出剖面的参数如下: (3) 除高度-航程参考曲线h(s)外,还需预先选定一条参考高度-动压剖面q(h).动压剖面的设计,可以在动压限制范围内以任意路径到达末端点.本文选择如图1所示的高度动压剖面形态.初末点已确定的前提下,通过3个参数(h1,h2,q1)确定动压随高度变化的曲线.其中,h1,h2如图1所示,q1表示高度h1,h2之间一段恒定的动压取值.本文采用固定h1,h2两点,仅通过调整q1来确定一条高度动压剖面. 图1 高度动压剖面Fig.1 Dynamic pressure profile 在给定的h(s)和q(h)下,按照待飞距等步长递推,首先解算出每一递推周期维持剖面所需的升力和阻力大小.对于无动力飞行器,其升力阻力受限于气动外形,很难保证递推过程处处严格按照设计的动压剖面运动,但纵向轨迹的设计目标需保证纵向剖面最后一阶段能满足末端约束.为此,后文描述了递推过程中,纵向剖面随飞行器升阻特性动态调整的具体方法. 递推过程中每周期由当前待飞距s,根据式(2)得到当前参考高度href.通过高度与待飞距的微分dh/ds=-tanγ,可以得到当前爬升角: Lref=(g-V2/r)cosγref/cosφ (4) 所示动压剖面给出了高度href对应的qref,可解得升力系数需求为:CLref=mLref/(Srefqref). 在忽略侧滑角及舵面影响时,飞行器的升力系数由攻角(α)、马赫数(mach)决定,升力系数为 CL=CL(mach,α) (5) 因此在空速给定的情况下,任一时刻的升力系数范围可知,当升力系数在飞行器能力范围内时,可以由式(5)反解出此时对应的攻角需求αref.记录本周期攻角α=αref,并根据剖面记录本周期的高度h(n)=h(s(n)).当升力系数的需求超过了飞行器能力范围时,需要对预设的高度参考剖面进行动态调整,具体调整步骤如①~⑤所示: ① 如果Lref ② 如果Lref>Lmax;令L=Lmax;计算对应的α. ④ 估算出本周期的高度值: ⑤ 令h0=h(n),γ0=γ(n),按式(3)更新高度剖面参数a10,a11,a12,a20,a21,a22. 完成高度剖面的一步递推/调整后,对动压剖面进行分析.递推过程中每周期根据预设的动压剖面qref=q(h(n)),可算出速度参考值Vref.近似求出阻力加速度的需求如下: 得到相应的阻力系数:CDref=mDref/(Srefqref). 在TAEM段可以通过阻力板偏转角(δSB)来调整阻力大小,从而实现对动压的控制,因此阻力系数是由马赫数、攻角和阻力板展开角度确定的: CD=CD(mach,α,δSB) 由于求解升力需求时已计算出相应的α,因此可以通过上式反解出CDref对应的δSB取值.当需要的阻力在飞行器能力范围之内时,则记录下本周期的V(n)=Vref、q(n)=qref及δSB.如果需要的阻力大小,超过了阻力板可控的范围,则按照如下步骤进行计算: ① 如果Dref ② 如果Dref>Dmax;令D=Dmax;计算对应的δSB. ③ 近似计算当前的速度和动压值: 为了保证递推末端点的动压满足末端约束,与高度剖面调整后更新整条参考曲线不同,动压调整后参考剖面不更新,在后续递推周期中,仍然按照预设的动压剖面计算阻力需求. 根据以上的递推步骤,如果递推至待飞距为零(s=0)时,飞行器高度和动压均维持在预设或动态调整后的剖面,即飞行状态满足TAEM末端约束条件,则这条轨迹线便是可行的. 显然,由于无动力飞行器能力的限制,可能存在递推结束时高度或动压仍无法跟踪纵向剖面的情况,则认为此时的航程和能量不匹配,判断本次递推的轨迹无效. 终上所述,单次递推时首先选择一个初始的s0为待飞航程,选择一个初始的q1确定动压剖面.按单位航程递推,令总递推步数为N,则每递推一次步长为Δs=s0/N.单次推衍流程如图2所示. 图2 单次纵向轨迹推衍流程Fig.2 Flowchart of single vertical trajectory propagation 随着轨道再入飞行器航程接近终点,飞行轨迹可调整的范围越来越小,轨迹跟踪的精度要求也越来越高.末端能量管理段飞行时间只有几百秒,航程调整范围一般只有几十公里.而初期再入段由于飞行时间长、飞行速度高,飞行器具备几百公里的航程调整能力.但初期再入段的控制能力相对较弱,末端散布较大.因此,确定一个好的标称TAEM起点,使得初期再入结束点的状态散布都处在末端能量管理段飞行能力可达的范围之内是十分重要的.本节通过对一个具体的再入飞行器递推结果进行分析,给出选择一条最优航程的方法,同时给出相应的最优高度动压剖面. 本节对动压剖面的参数q1和初始待飞距s两个参数进行分析.本文算例中飞行器TAEM段初始标称状态为:VE=750 m/s,hE=29 km,γE=-6°;自动着陆起点状态:qf=10 kPa,hf=4 km,γf=-14°.递推过程中考虑如下的近似条件: (1) 升力系数只受攻角马赫数影响,阻力系数则同时考虑攻角、马赫数以及阻力板的影响. (2) 由于纵向轨迹递推过程不考虑地面轨迹,因此精确的倾侧角大小无法确定,递推过程中以均值近似. 设计动压剖面q1=12 kPa,分别在90 km,110 km,120 km航程情况下进行递推.曲线如图3~4所示.根据动压递推曲线可知在飞行初期,动压比较难维持在理想的参考剖面.但到TAEM中后期,高度低于13 km以后,90 km航程的动压曲线可以保持在预设的参考动压曲线上.高度10 km以下,110 km和120 km航程的递推曲线,也维持在了预设的动压曲线上.图5为递推过程中阻力板展开比例,其中阻力板展开比例的定义如下: κSB=(δSB-δSBmin)/(δSBmax-δSBmin) 式中δSB为阻力板展开角度,δSBmin及δSBmax分别为阻力板允许的最大展开角度和最小展开角度.当阻力板保持最大角度时κSB=1,反之κSB=0.从图5也可以看出,轨迹递推初期,阻力板较长时间处于极限展开值. 重新设定q1=8 kPa的动压剖面,针对以上3种航程递推,结果如图6~8所示.对8 kPa的动压剖面,航程120 km的轨迹比90 km和110 km的轨迹更早维持在了预设的动压剖面上.产生这个现象的原因在于,当飞行航程较短时,飞行器轨迹更陡,平均的航迹倾侧角γ更小,飞行器的平均下降率更快,因此动压处于较高的水平.反之,动压则处于较低的水平.综上可知:对于不同的动压剖面,存在不同的与之匹配的最优航程. 图3 高度-待飞距曲线(q1=12 kPa)Fig.3 Height range profile(q1=12 kPa) 图4 高度-动压剖面(q1=12 kPa)Fig.4 Aerodynamic press profile(q1=12 kPa) 图5 阻力板展开比例(q1=12 kPa)Fig.5 Speed brake ratio(q1=12 kPa) 图6 高度-待飞距曲线(q1=8 kPa)Fig.6 Height range profile(q1=8 kPa) 图7 高度-动压剖面(q1=8 kPa)Fig.7 Aerodynamic press profile(q1=8 kPa) 图8 阻力板展开比例(q1=8 kPa)Fig.8 Speed brake ratio(q1=8 kPa) 从实际飞行的角度考虑,飞行过程中阻力板尽量维持在中间状态,则飞行器的阻力系数在正负方向均具备一定的调节能力.这种情况下的弹道比阻力板始终处于极限情况的弹道更具有鲁棒性.因此阻力板状态可以作为对一条弹道是否具有鲁棒性的判据,本文选择如下所示的指标函数,以最小化指标函数为目标优选纵向弹道. 上式中CDMax,CDMiddle,CDMin分别为飞行器阻力板置于最大值,中点值以及最小值时对应的阻力系数.从上式可以看出,如果全程阻力系数参考值都处于中间值,则得到最理想的状况即J=0;如果全程都处于极大值,或极小值,则J=1.0.为得到最优的航程与最匹配的剖面,本文针对动压剖面参数q1和航程s双参数进行寻优.首先固定动压剖面参数q1,得到当前动压下指标最优的航程s,以及此时对应的指标值J.再以固定步长遍历q1,得到每一个动压下对应的最优航程和相应的J,从而得到全局最优的动压剖面和航程.本算例中选择以100 Pa为步长遍历q1,以1.5 km为步长遍历航程s0,按图2所示的流程递推纵向轨迹,若该条弹道为可行解,则存储相应的数据.图9~10为遍历的纵向剖面.图11为所有存储的可行弹道在不同动压下最优航程以及相应的J取值.根据递推的仿真结果可以看出,随着动压剖面参数q1取值增大,对应的最优航程大致趋势是减小.但不同动压剖面取得的最优指标值J的取值则是呈V型曲线,在约11 kPa的动压时取得最小值,此时对应的航程约117 km. 图9 遍历的高度动压剖面Fig.9 Aerodynamic press profile of ergodic propagation 图10 遍历的高度航程剖面Fig.10 Height range profile of ergodic propagation 综上,可以将此算例TAEM段的标称待飞航程设计为117 km,通过地面几何可以确定一个标称的起点.而标称的动压剖面则按图11所示的剖面形状,选择参数q1=11 kPa. 图11 不同动压剖面下最优指标航程曲线Fig.11 Best range for specified aerodynamic pressure 图12 地面轨迹几何示意图Fig.12 Ground trajectory geometry 本文的主要目标是优化纵向剖面,考虑到一个具有较强鲁棒性的纵向轨迹可以适应飞行器航程在一定范围内的调整,因此本文不再动态规划地面轨迹线. 为验证优化的纵向剖面的鲁棒性,本文对飞行器六自由度动力学进行打靶仿真.仿真初始状态和散布如表 1所示.仿真中,采用本文优化得到的纵向剖面为参考跟踪轨迹.飞行过程中,按PD控制律调整攻角以实现高度跟踪,动压跟踪则靠阻力板偏转角度实现.仿真结果如图13~15所示. 表1 偏差条件Tab.1 Windage condition 图13 打靶仿真地面轨迹线Fig.13 Ground trajectory of Monte Carlo simulation 图14 打靶仿真高度变化曲线Fig.14 Height profile of Monte Carlo simulation 图15 打靶仿真高度-动压曲线Fig.15 Aerodynamic pressure profile ofMonte Carlo simulation 对于无动力再入飞行器,其飞行轨迹的设计不管是在初期再入段、末端能量管理段还是着陆段,都需要在明确飞行器升阻特性的基础上进行优化.本文通过设计不同的动压剖面和待飞距,对飞行器纵向剖面进行数值递推.针对所有的可行轨迹,以阻力板控制裕度最大为目标优选出最合适的纵向剖面以及最优的待飞距.通过对考虑初始状态偏差、气动偏差情况下的六自由度打靶仿真,验证了本方法所确定的剖面的鲁棒性.2 轨迹递推方案
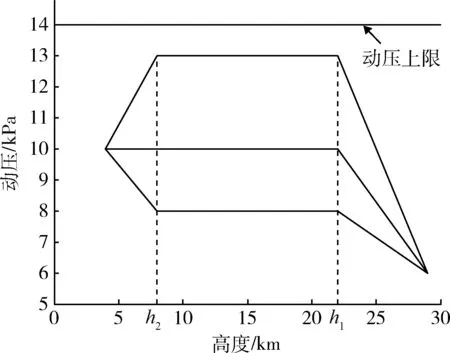
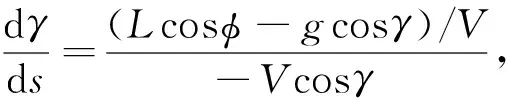
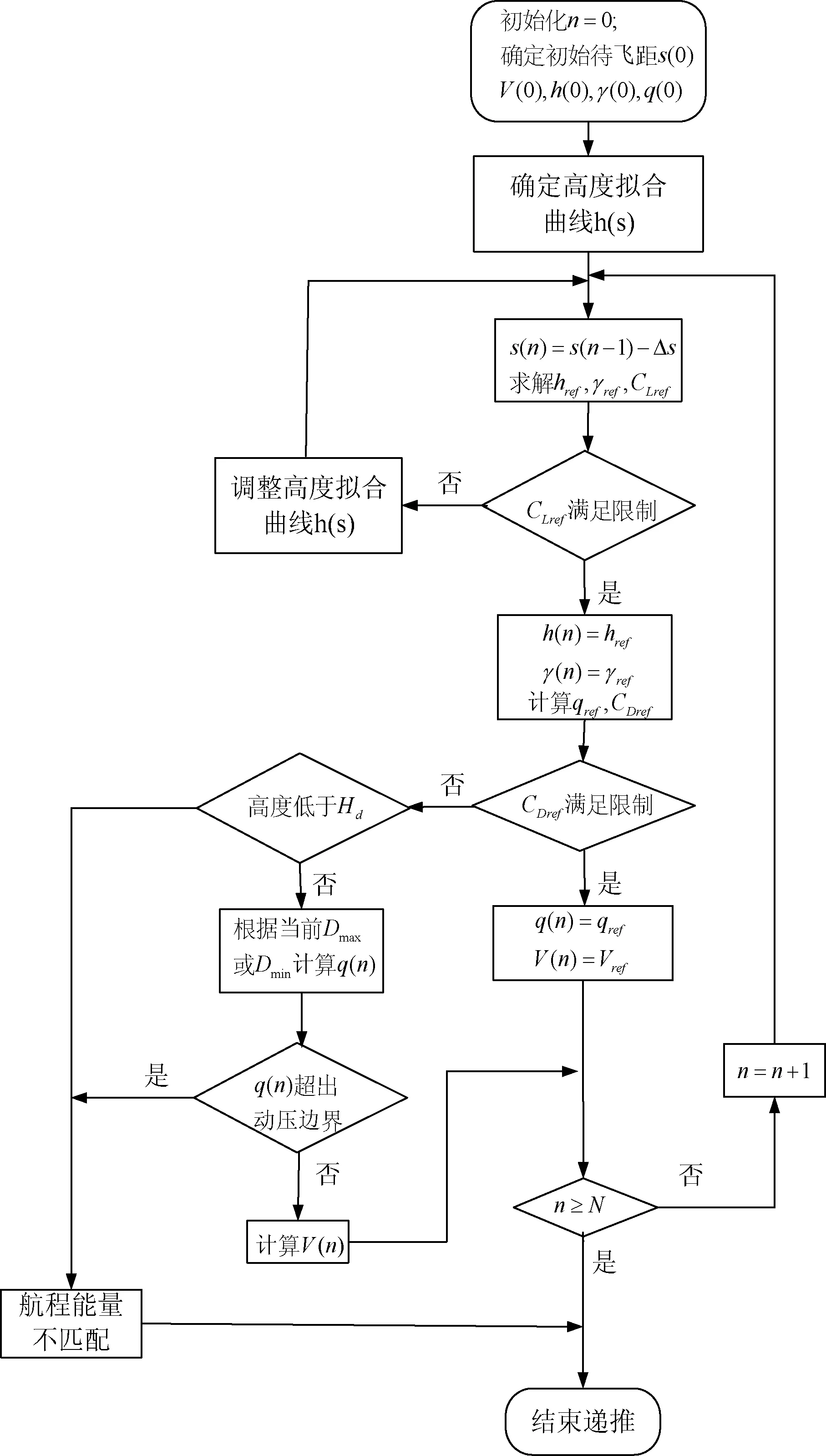
3 纵向剖面优选
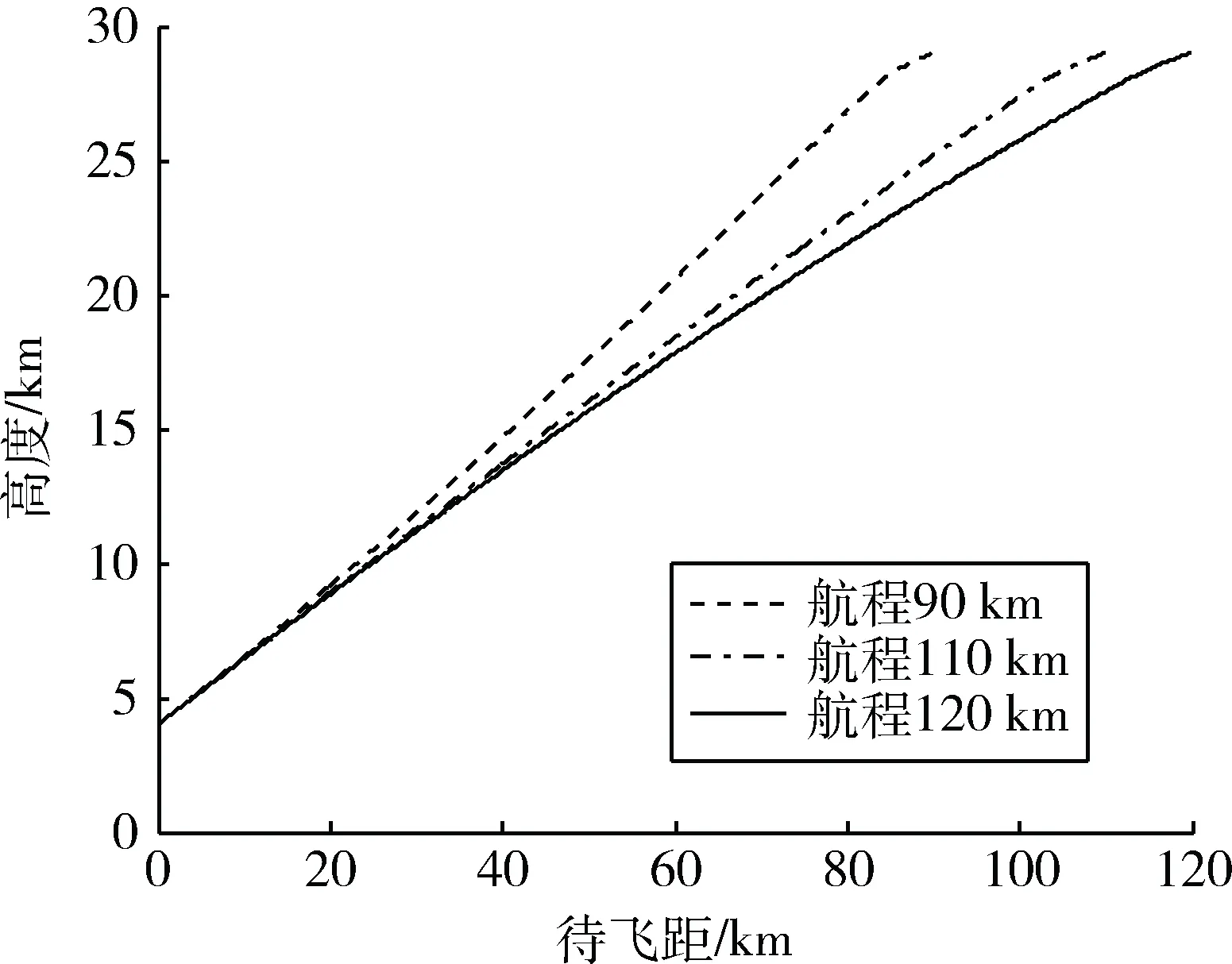
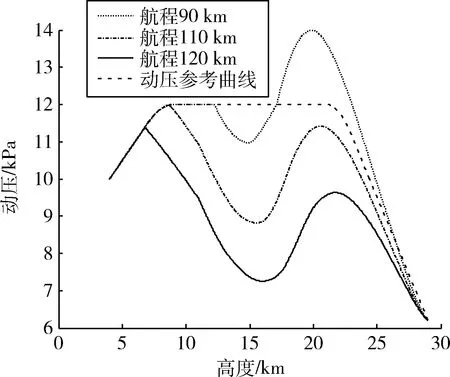
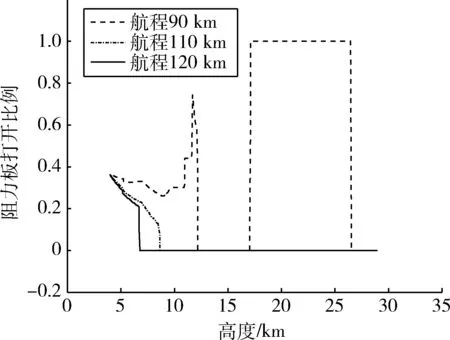
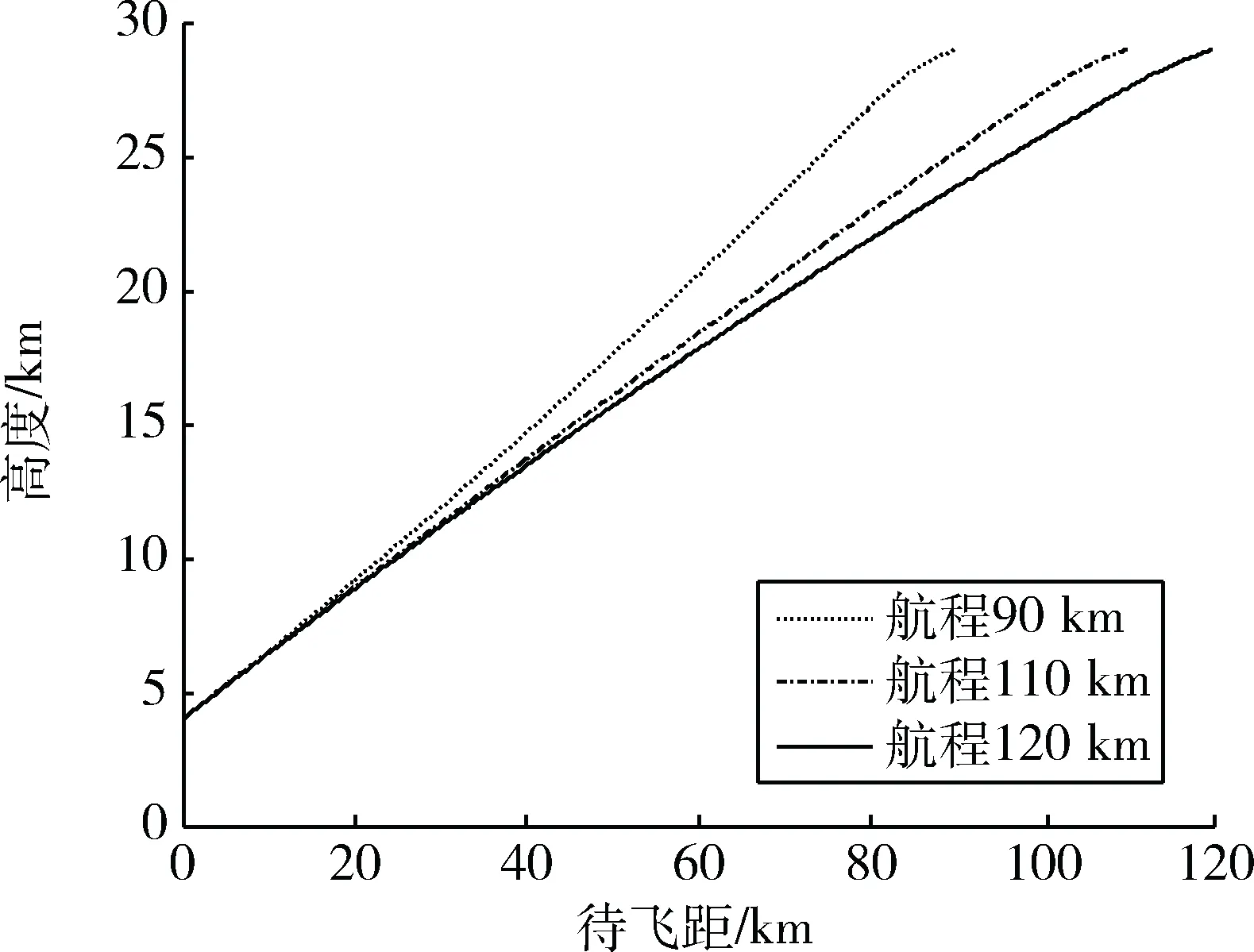
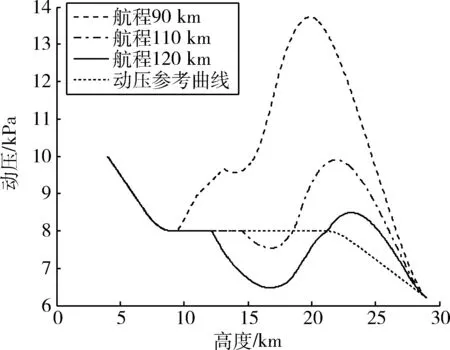
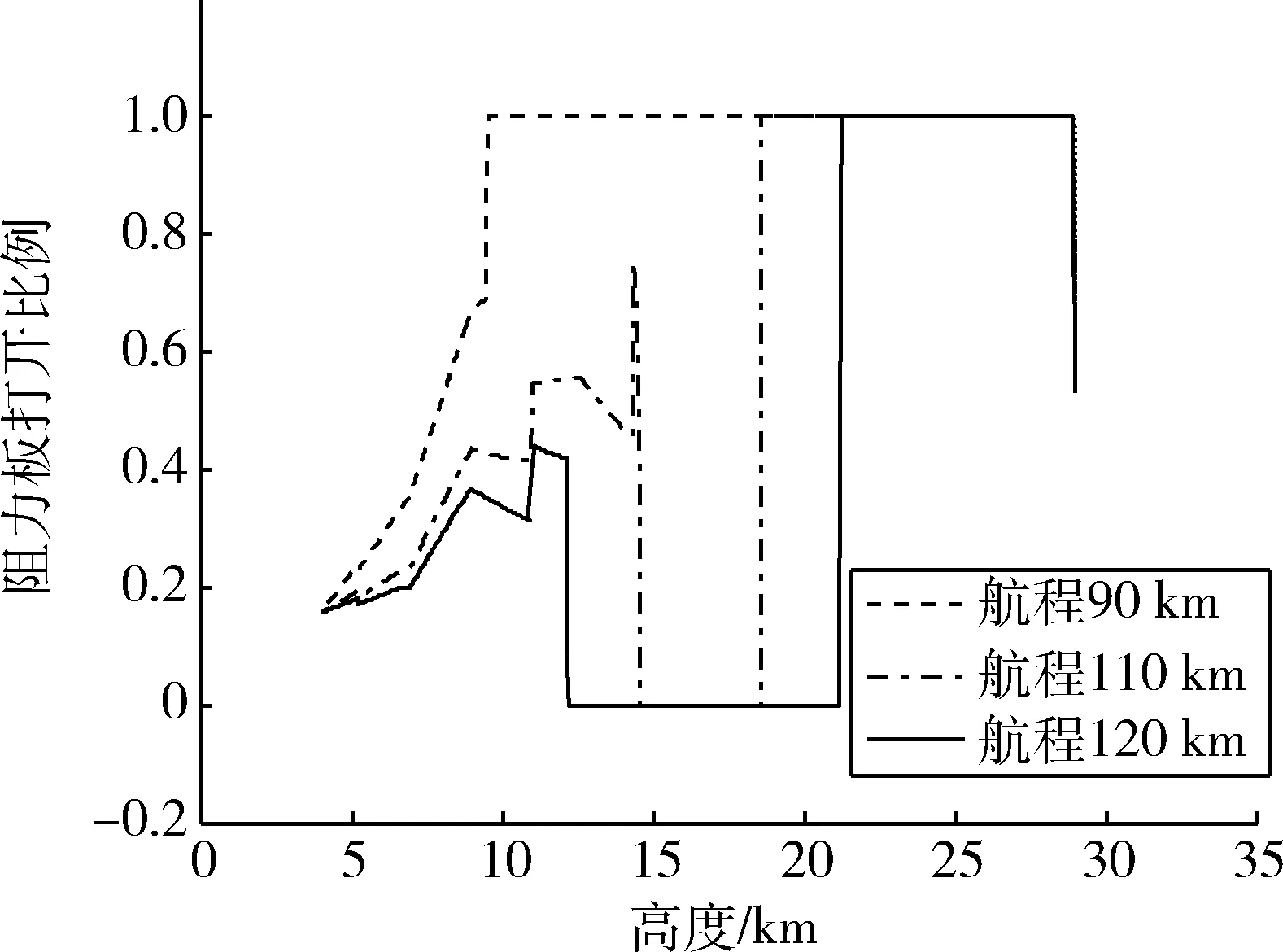
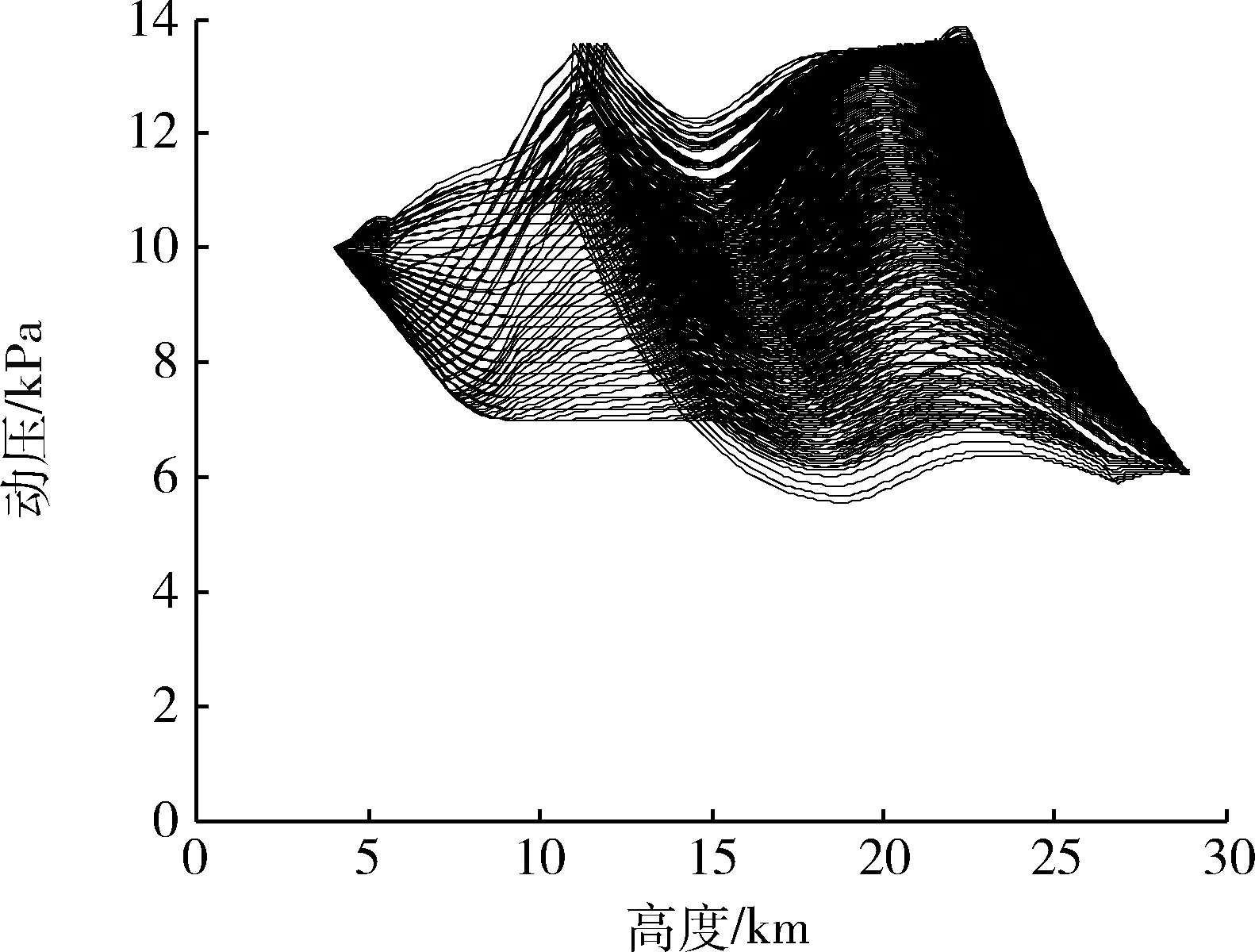
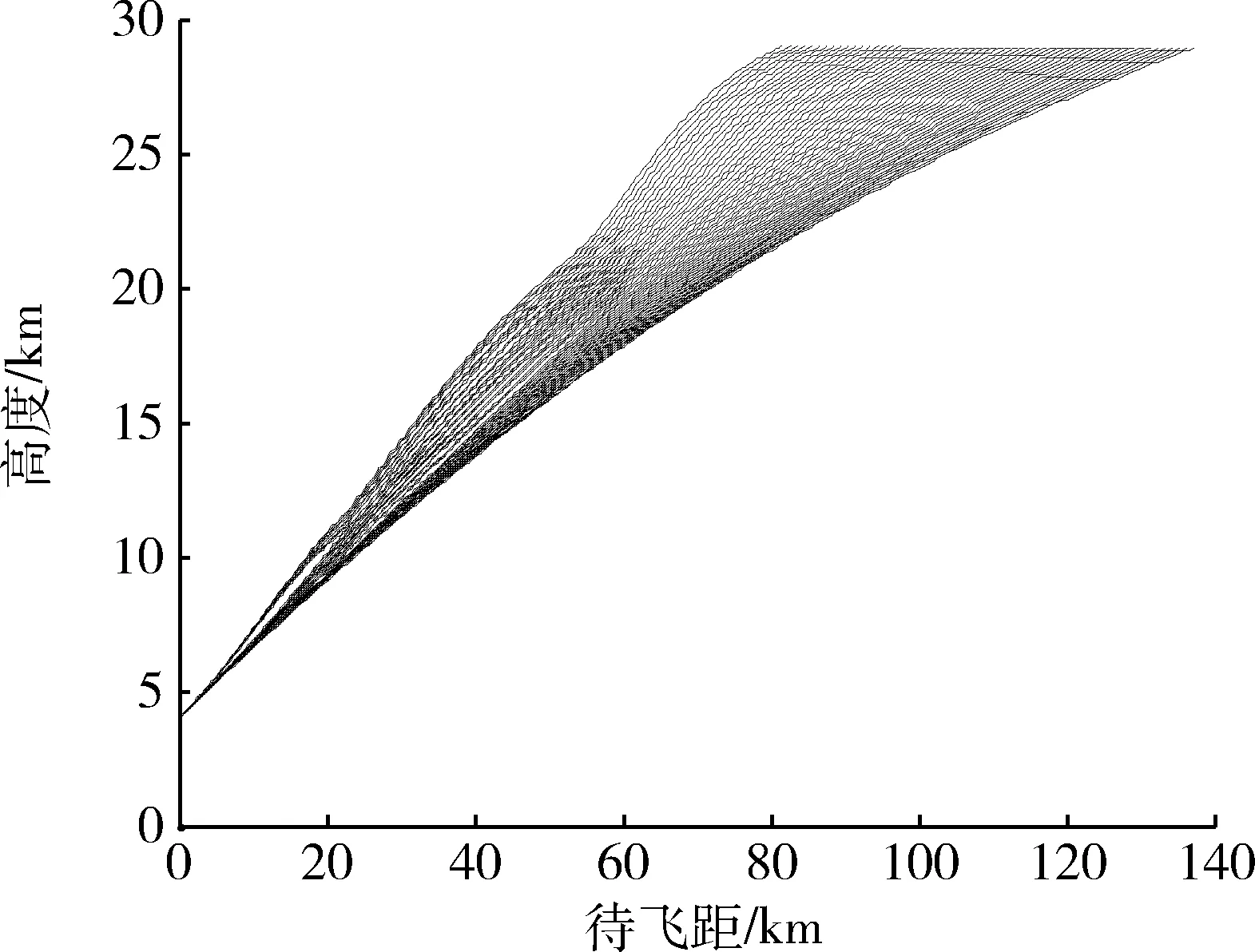

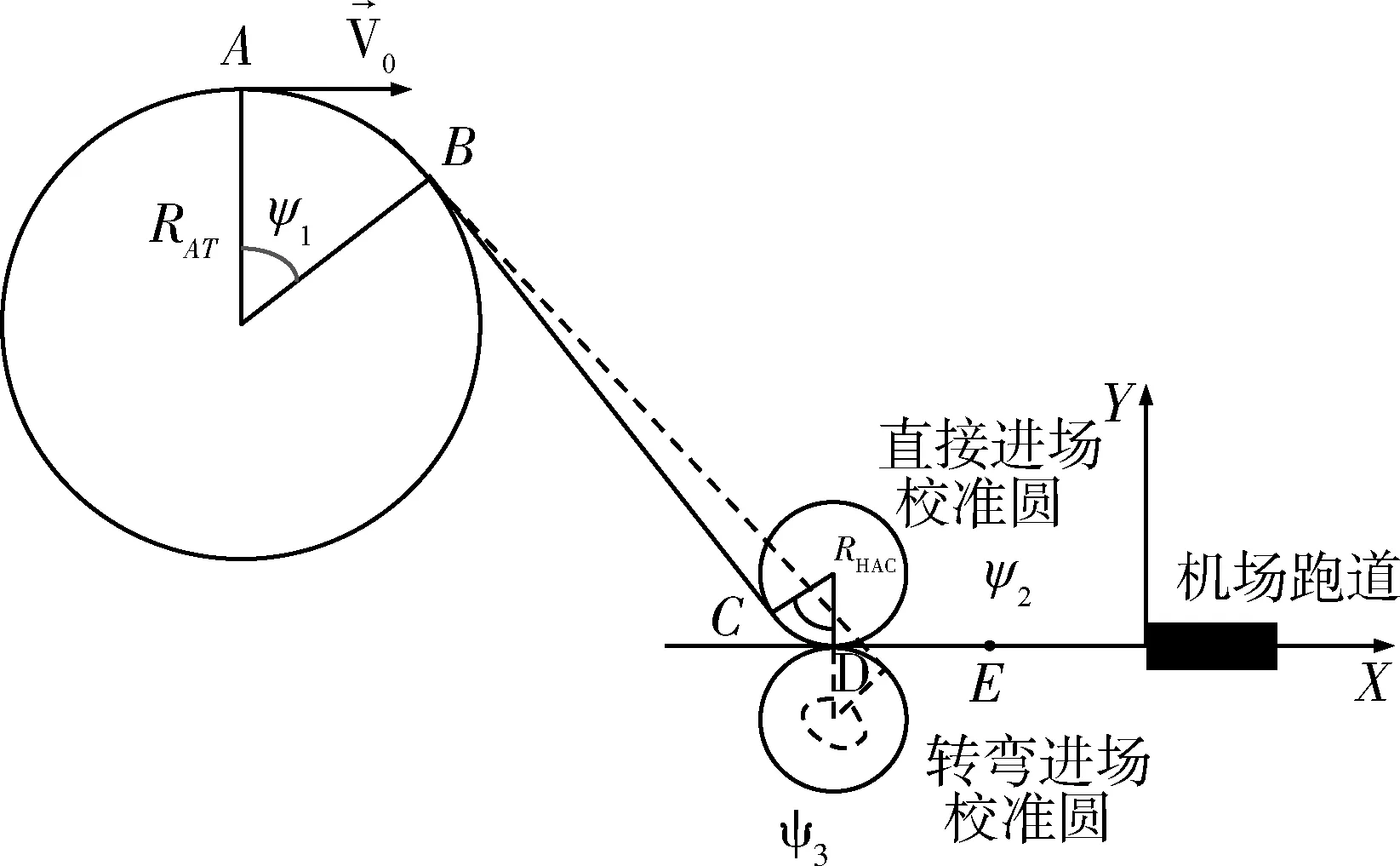
4 水平轨迹
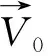
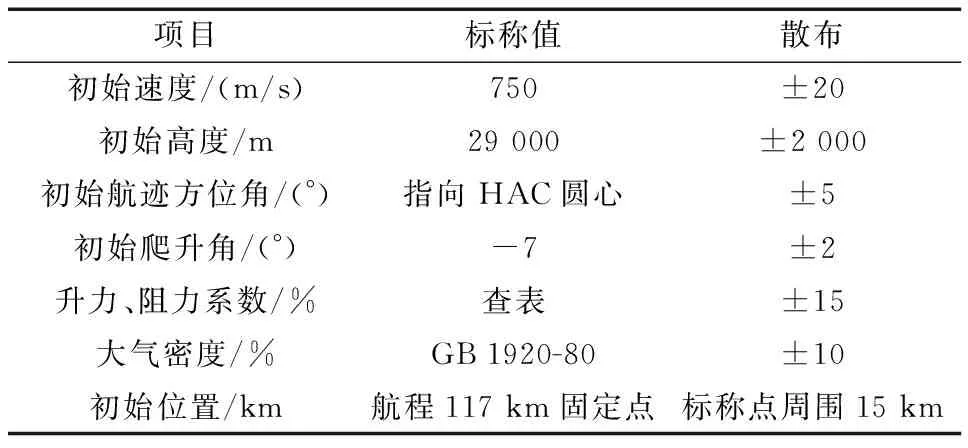
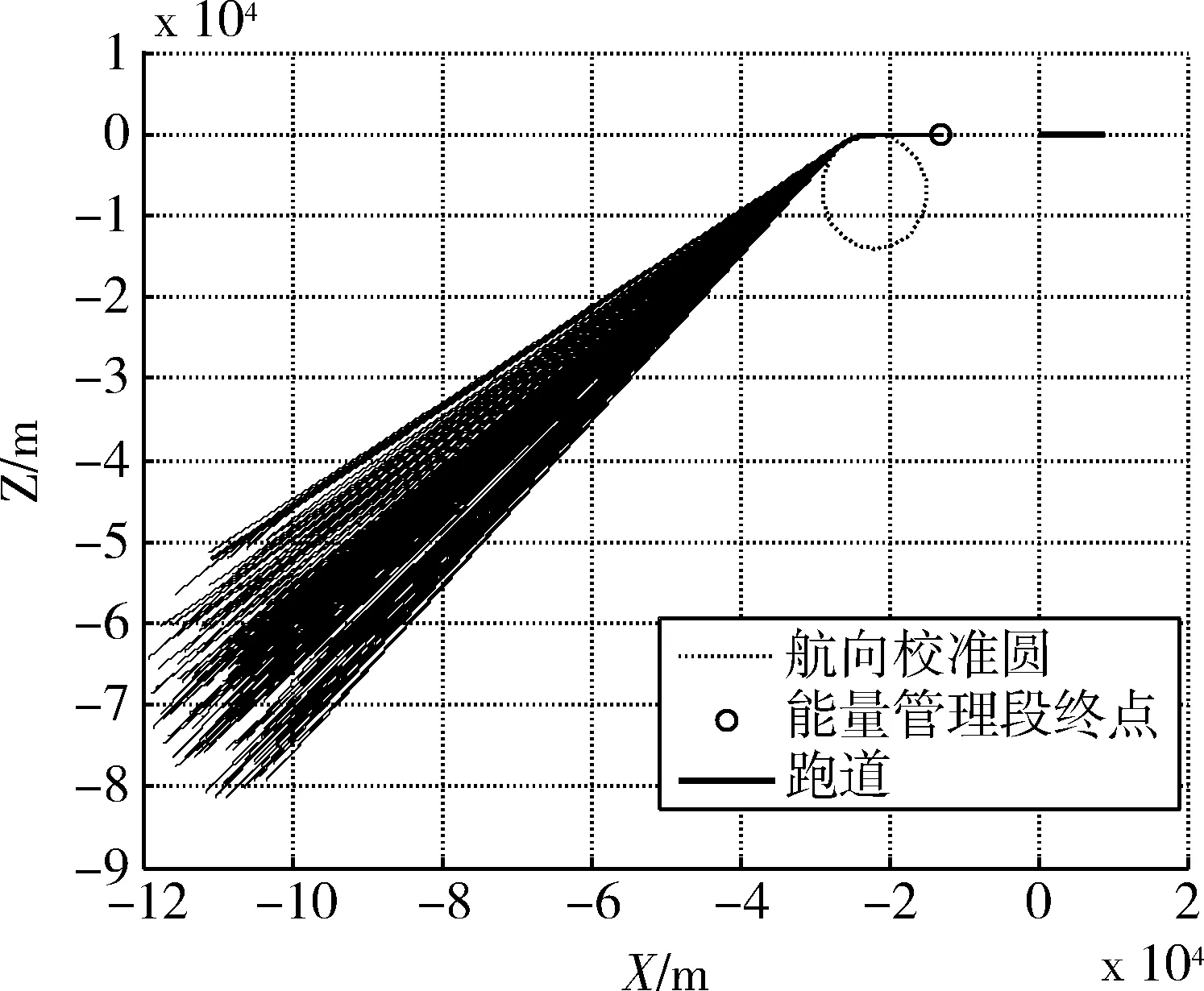
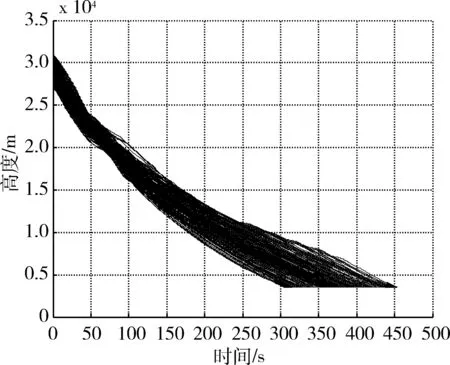
5 仿真结果
6 结 论
