基于多目标遗传算法的反舰导弹中制导惯组精度优化分配方法

王 兴 赵长见 梁 卓 吕 瑞

中国运载火箭技术研究院，北京 100076

采用“惯组中制导+主动雷达末制导”复合制导的机载反舰导弹，由于载机平台的姿态误差、传递对准误差、惯性器件误差、目标指示误差和目标逃逸误差等因素影响，可能导致导弹中末制导交班时不一定能捕获到目标[1]。因此，在研制阶段，需要对影响中末制导交班精度的误差源进行分析，并确定各项误差源的灵敏度，即进行制导精度分配。

目前精度分配方法主要有：蒙特卡罗法、协方差分析法和线性化伴随法。文献[2]将方差分析法与蒙特卡洛法结合，舍弃对精度影响较小的误差源，模型相对较简单。文献[3]将改进的粒子群优化算法与蒙特卡罗打靶结合，进行末制导精度分配，但目标函数设置简单。近年来还陆续出现了基于数学模型的精度分配方法、基于模糊综合评判的精度分配方法和基于价值分析的精度分配方法，但需要精确的模型来描述精度分配问题[4]。

中制导精度以顺利实现中末制导交班为约束，而影响中制导精度的因素有多项误差。在同一中制导精度条件下，精度分配有多种组合，如何在满足精度要求的前提下实现成本最优化是本文研究的问题。

中制导精度优化分配问题，可转化为求一系列允许最优误差指标，使导弹满足中末制导交班条件，本质是多目标优化问题。

遗传算法(Genetic Algorithm，GA)是模拟生物在自然环境中“物竞天择，适者生存”规则而演化形成的一种随机优化搜索算法，它具有较强的全局搜索功能和求解问题的能力[5]。常用的多目标遗传算法有向量评估多目标遗传算法、基于目标加权法的遗传算法、多目标粒子群算法、微遗传算法、非支配排序法(Non-dominated Sorting Genetic Algorithm， NSGA)以及带精英选择策略的快速非支配排序法(NSGA-II)等[6]。其中NSGA-II算法是K.Deb等学者[7]在NSGA的基础上改进的，改进主要体现在3个方面：1)采用了更为高效的排序过程；2)提出了拥挤度和拥挤度比较算子，使Pareto解集均匀分布，保持了种群的多样性；3)引入精英策略，扩大采样空间，使得最佳个体不会丢失；NSGA-II算法效率高、收敛性好，特别适合多目标问题求解[8]。

提出了一种基于多目标遗传算法的机载反舰导弹中制导精度优化分配方法。首先，分析影响中末制导交班的主要误差因素，将导弹自身的中制导误差、目标指示误差等效为目标机动误差，建立了中末制导交班模型；然后，依据误差实现的技术难度、成本等综合指标建立了指标实现的代价函数；最后，采用多目标遗传算法NSGA-II实现中制导惯组工具误差精度优化分配。

1 中/末制导交班建模

1.1 影响中末制导的主要因素分析

中末制导能否实现顺利交班，主要取决于末制导雷达开机时目标是否处于雷达视场中。影响导弹捕获概率的主要因素有：导弹自身的中制导误差、目标指示误差、目标机动误差以及雷达探测能力等。

1.1.1 导弹中制导误差

导弹中制导误差是指末制导雷达实际开机点相对理论开机点的随机误差，影响导弹自身中制导误差的主要因素包括：制导方法误差、载机平台误差、传递对准误差和惯组工具误差等。由于制导方法误差量级为米级，对中末制导影响较小，因此可忽略。

1)载机平台误差

载机平台上的输出信息的精度是影响传递对准性能的关键因素，载机平台精度主要包括：载机位置精度、载机速度精度、载机姿态精度。载机平台的位置和速度对准精度较高，误差可以忽略；而载机姿态(俯仰角精度φ′，航向角精度ψ′，载机滚动角精度γ′)误差对中制导误差影响较大，必须考虑。

2)传递对准误差

初始误差是惯导系统的一个重要误差来源，所以初始对准的精度直接影响惯导系统的性能[9]。位置和速度对准精度较高，误差可以忽略；姿态对准误差对中末制导精度的影响较大。在扣除载机误差的条件下，传递对准对误差角的精度为：俯仰角精度φ″，航向角精度ψ″，滚动角精度γ″。

3)惯组工具误差

导弹采用惯组中制导模式，中制导飞行时间长、距离远，制导系统的积累误差大，因此，必须考虑惯组工具误差对中制导的影响。惯组工具误差模型较为复杂，工程上常用简化的误差模型来分析惯组工具误差对导弹飞行的影响，惯组工具误差模型如下[10]：

陀螺误差的简化模型为：

(1)

式中，D0x，D0y和D0z为陀螺零漂；kgx，kgy和kgz为陀螺比例系数误差；Eyx，Ezx，Exy，Ezy，Exz和Eyz为陀螺安装误差。

加速度计误差模型为：

(2)

式中，k0x，k0y和k0z为加速度计零位误差；kx，ky和kz为加速度计比例系数误差；Eayx，Eazx，Eaxy，Eazy，Eaxz和Eayz为加速度计安装误差，k2x，k2y和k2z为加速度计二次项系数误差。

假设以上各项误差源之间不相关，则导弹中制导位置误差(ΔxM,ΔyM,ΔzM)服从高斯分布，由于高度方向的误差ΔyM较小，可不考虑。因此导弹自身中末制导误差在一个水平面上，圆的概率分布模型为：

(3)

其中，标准差σM为：

(4)

其中，N为误差源的总个数；i代表各项误差，分布参数可以根据蒙特卡洛仿真确定。

1.1.2 目标的指示误差

目标的指示误差主要由导引平台指示误差和时间延迟误差2部分组成。

1)导引平台指示误差

引导平台指具有超视距引导能力的飞机、舰艇、卫星等，导引平台指示误差是指导引平台的探测误差，导引平台最大误差为ΔRPT，则可设导引平台误差分布可近似为正态分布，即：

(5)

式中，σPT=RPT/3。

2)时间延迟误差

时间延迟误差指从探测到目标至上传信息到导弹的延迟时间所导致的误差。如果τ1为信息传输延迟时间，则时间延迟导致的误差半径ΔRYC可近似正态分布，即：

(6)

式中，σYC=Vmax·τ1/3，Vmax为舰船最大的航行速度。

1.1.3 目标机动误差

从导弹发射到末制导雷达开机，中制导飞行时间t较长，目标在此时间段内机动将导致的指示误差、目标机动误差的圆半径ΔRJD服从下列正态分布：

(7)

式中，σJD=Vmax·t/3。

1.2 中末制导交班时刻等效综合偏差

中末制导交班主要取决于导弹与目标之间的相对位置关系，因此，导弹自身的中制导误差和目标指示误差可等效为目标附加的机动误差。因此目标的等效机动圆的半径ΔR服从下列高斯分布：

ΔR～N(0,σR)

(8)

式中，

(9)

由于服从正态分布的N(μ,σ)的随机变量几乎不会在以(μ-3σ,μ+3σ)之外取值，因此中末制导交班目标相对导弹的位置可以近似降落在一个圆形范围之内，圆半径R为：

R=3σR

(10)

1.3 雷达探测能力

中末制导交班时刻等效综合偏差为半径为R圆域，雷达视场范围如图1所示。

图1 末制导雷达探测区域示意图

图中，Rmax为雷达导引头最大作用距离；η为雷达半视场角；H为导弹飞行高度。导引头探测的椭圆区域ABCD的长半轴a和短半轴b为：

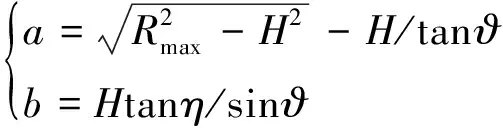
(11)

式中，ϑ=π/2-(arccos(H/Rmax)-η)，为雷达视线中心与水平面的夹角。

由图1可知，雷达导引头捕获目标的概率可近似为：

(12)

式中，Φ(x)表示正态分布函数。

由此可知，在雷达作用距离Rmax及半视场角η给定的情况下，目标等效误差圆半径的散布方差σR决定雷达捕获目标的概率。

2 制导精度优化分配方法

2.1 中制导精度优化分配问题的转化

基于中末制导交班建模研究可知，中末制导交班能力取决于中末制导交班时刻等效综合偏差和雷达探测能力的相对大小，而目标指示误差受探测平台精度的影响，目标机动误差与舰船机动能力相关，载机平台姿态误差受载机上的惯组器件精度影响，传递对准误差与对准算法能力有关，可认为其在当前阶段保持不变。以上各项误差都是外界对反舰导弹的设计约束，而反舰导弹无法改变；本文只针对影响导弹中制导误差的惯组工具误差进行优化分配，为惯组指标选型提供支撑。

2.2 基于权系数矩阵的指标实现代价建模

采用基于权系数矩阵方法对惯组指标实现代价进行建模，具体如下。

惯组工具误差指标实现的代价ci根据技术实现的技术难度、成本等综合指标确定，具体可以通过调研目前惯组产品的指标与技术难度、成本之间的关系，并通过函数关系拟合出来(本文不做详细研究)。本文将指标难度系数分为5个等级，代价系数在每一等级内线性变化，代价等级和代价系数关系如表 1所示。

表1 误差指标实现的代价等级和代价系数

误差指标实现的总代价Jc定义为各项误差指标难度系数加权平均数，即：

(13)

式中，ci为各项误差指标实现的代价；N为待分配误差指标个数。

精度分配问题等价为在满足中末制导交班条件的前提下，误差指标实现代价函数Jc取最小值。因此，可取下列两项指标为优化目标：

(14)

式中，J1为指标实现的总代价；P为中末制导交班成功概率；J2为中末制导交班失败概率。

2.3 基于多目标遗传算法的精度优化分配

本文提出的基于多目标遗传算法的机载反舰导弹中制导精度优化分配方法，首先建立机载反舰导弹中末制导精度优化模型，然后利用NSGA-II算法求解机载反舰导弹精度优化分配问题，具体方法如下：

1)建立中末制导精度优化模型。首先建立中末制导交班模型，然后依据惯组工具误差的技术实现难度、经济花费大小等建立实现代价模型；

2)初始化种群。随机初始化个体数为N的种群Pt，并将所有个体按非支配关系排序且计算适应度值；

3)利用遗传操作选择、交叉和变异产生新种群Qt；

4)种群合并得种群Rt。将种群Pt和种群Qt两个群体的次序打乱并合并成群体Rt，群体大小为2N；

5)非支配排序。采用快速非劣排序算法将种群Rt中的个体划分成不同的非劣级别；

6)产生新种群Pt+1。按非支配等级把分层的个体放入子代种群的容器中，该种群的大小为N；

7)判断是否满足遗传算法的终止条件，若满足，则退出遗传算法，并得到Pareto最优解；否则继续执行步骤3。

图2 遗传算法中制导精度分配计算流程图

3 仿真算例

以某反舰导弹为例，目标指示误差、目标机动误差及载机平台姿态误差是反舰导弹的外界设计约束，传递对准误差与对准算法能力有关，可认为其在当前阶段保持不变，仅对影响导弹中制导误差的惯组工具误差进行优化分配，为惯组指标选型提供支撑。

陀螺和加速度计的相对误差系数(以最大值为基准归一化处理)与代价系数之间关系如图3和4所示。

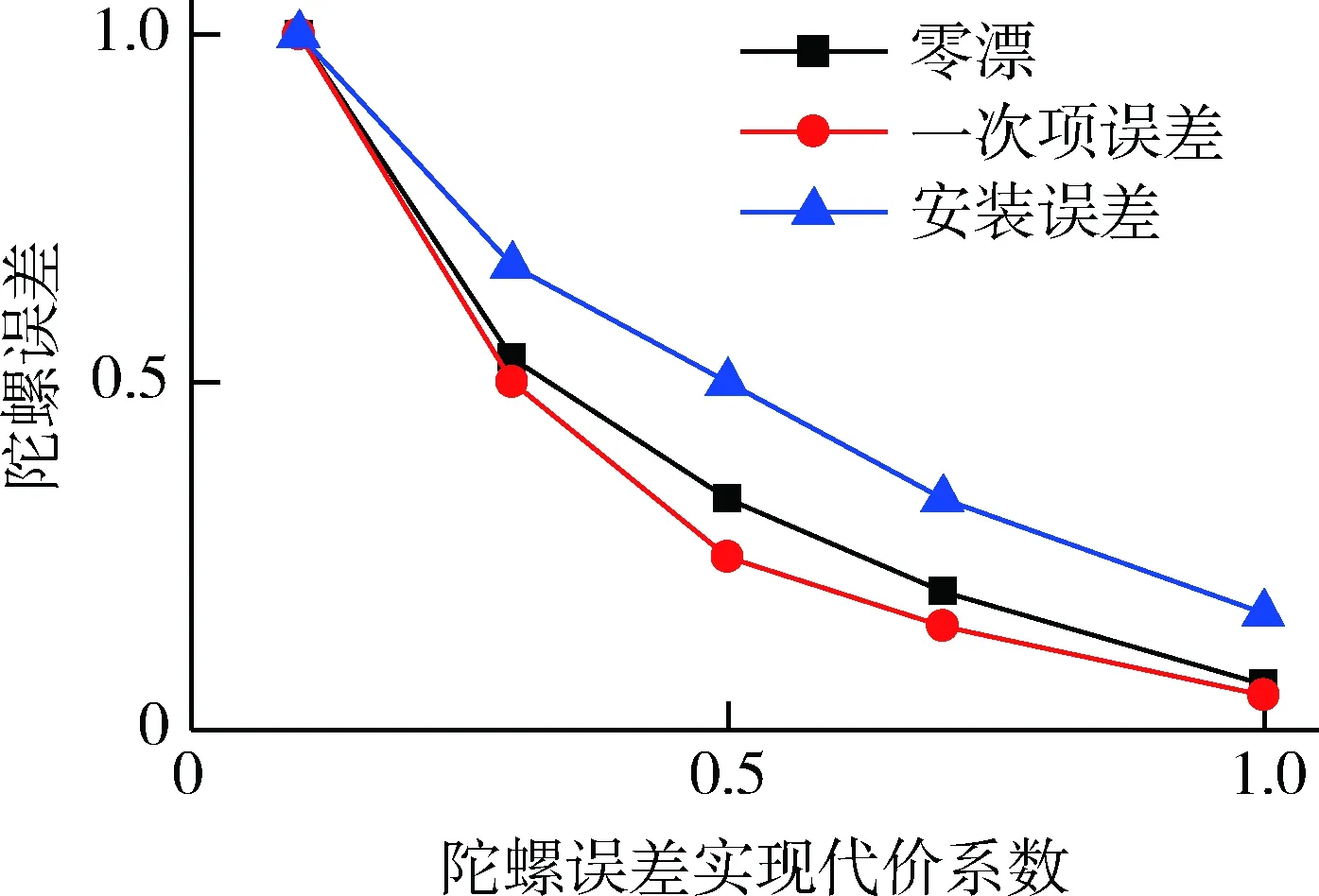
图3 陀螺相对误差与代价系数的关系

图4 加速度计相对误差与代价系数之间的关系

遗传算法的种群大小为100，最优前端个体系数为0.1。NSGA-II遗传算法得到的Pareto最优解如图5所示。

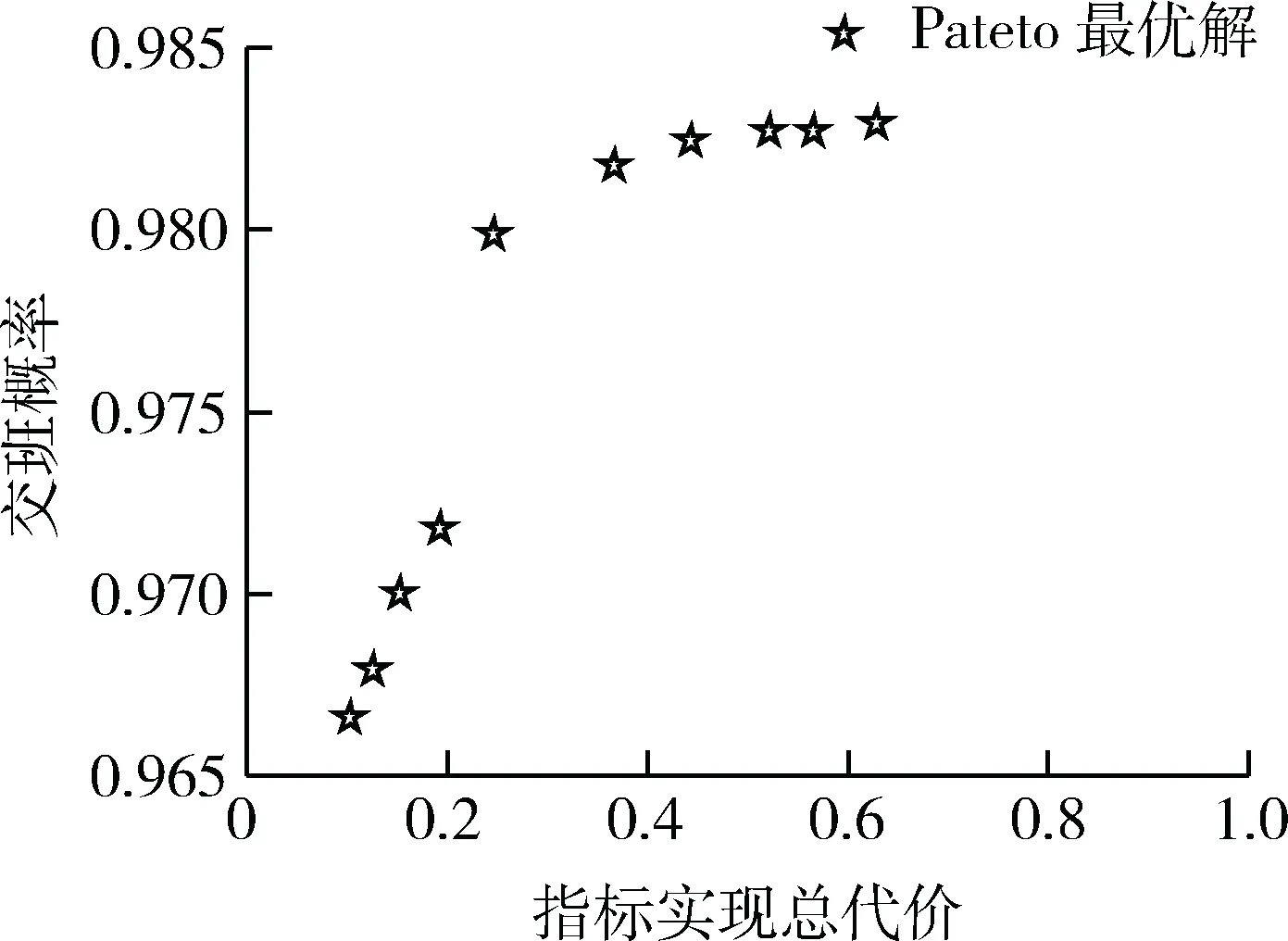
图5 指标实现总代价与交班概率的关系图

由图5可知，Pareto最优解的交班概率均在96.5%以上，中末制导交班概率较高。选取Pareto最优解中交班概率较高且指标实现总代价较小的个体3、4、5进行分析，其误差指标分配结果(已归一化处理)如表2所示。

由表2可知，Pareto最优解3、4、5中交班概率相差较小，但是Pareto最优解3精度要求相对低，指标实现代价更小。因此，选取Pareto最优解3为最优个体，其惯组工具误差指标为最优分配指标。

表2 Pareto解的误差指标分配结果

将最优个体3各项误差源加入模型中并进行蒙特卡罗仿真，仿真结果(以雷达探测半径为基准进行归一化处理)如图6所示。

图6 中末制导交班位置蒙特卡罗仿真结果

由仿真结果可知，中末制导的交班成功概率达98.2%，因此，基于遗传算法的惯组工具误差分配方案能满足中末制导交班要求。

4 结论

针对机载反舰导弹中制导精度分配方法进行了研究。首先，分析影响中末制导交班的主要误差因素，将导弹自身的中制导误差、目标指示误差等效为目标机动误差，建立了中末制导交班模型；然后，依据误差实现的技术难度、成本等综合指标建立了指标实现的代价函数；最后，采用多目标遗传算法实现中制导惯组工具误差精度分配。仿真结果表明，本文提出的基于遗传算法的反舰导弹中制导精度分配方法能保证中末制导交班条件和误差指标实现的代价最小。同时该方法简单、适用性强，能为实际工程的惯组的合理选型提供设计依据。

参 考 文 献

[1] 赵辉, 沈闽锋, 许士海. 反舰导弹超视距攻击捕捉概率模型研究[J]. 舰船电子工程, 2008(1)： 56-58. (Zhao Hui, Shen Minfeng, Xu Shihai. Studies on Model of Target-Catching Probability for Anti-ship Missle Over-the-horizon Attack [J]. Ship Electronic Engineeing, 2008(1)： 56-58.)

[2] 尚云磊, 唐硕. 基于方差分析的Monte- Carlo制导精度分配方法研究[J]. 飞行力学, 2009, 27(3): 93-96. (Shang Yunlei, Tang Shuo. Research on the Guidance Precision Distribution Method Based on the Variance Analysis [J]. Flight Dynamics, 2009, 27(3): 93-96.)

[3] 彭燕荣, 杜昌平, 王月星. 基于改进 PSO 的导弹制导精度分配[J]. 计算机应用, 2013, 33 (S2): 102-104.(Peng Yanrong, Du Changping, Wang Yuexing. Precision Distribution Method of Missile Guidance Based on Improved Particle Swarm Optimization [J]. Journal of Computer Applications, 2013, 33(S2): 102 -104.)

[4] 陈杰, 窦丽华, 张佳. 基于综合集成理论的一类典型复杂系统精度分配研究[C]. 第25届中国控制会议, 哈尔滨, 2006: 352-355.(Chen Jie，Dou Lihua，Zhang Jia. Accuracy Assignment Research of a Typical Complex System Based on Meta- Synthesis Theory [C]. Proeeedings of the 25th Chnese Control Conferenee, Harbin, 2006 :352- 355.)

[5] Holland J H. Adapation in Naturaland Artificial Systems [J]. The University of Michigan Press, 1975 (1) : 21- 24.

[6] 马小姝, 李宇龙, 严浪. 传统多目标优化方法和多目标遗传算法的比较综述[J]. 电气传动自动化,2010, 32 (3): 48-50.( Ma Xiaoshu, Li Yulong, Yan Lang. Comparion Review of Traditional Multi-objective Optimition Methods and Multiobjective Genetic Algorithm[J]. Electric Drive Automation ,2010, 32(3),: 48-50.)

[7] Deb K., Pratap A., Agarwal S., Meyarivan T., A Fast and Elitist Multiobjeetive Genetie Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2000, 6(2): 182-197.

[8] 张福威, 李军, 孟品超等. 多目标进化算法综述[J]. 长春理工大学学报,2012, 35(3): 103-105. (Zhang Fuwei, Li Jun, Meng Pinchao, et al. Survey of Multi-objective Evolutionary Algorithms [J], Journal of Changchun University of Science and Technology, 2012, 35(3): 103-105.)

[9] 宋嘉钰, 杨黎明, 李东杰．惯性导航传递对准技术发展现状与趋势[J]． 兵器装备工程学报, 2016, 37(2): 139-143. (Song Jiayu, Yang Liming, Li Dongjie. Development of Transfer Alignment for Inertial Navigation Systems [J]. Journa of Ordnance Equipment Engineering, 2016, 37(2): 139- 143.)

[10] 胡小平. 自主导航技术[M]. 北京: 国防工业出版社, 2016.(Hu Xiaoping, Autonomous Navigation Technology [M]. Beijing: Natianal Defense Industry Press, 2016.)