一种机械臂终端滑模控制方法*

崔 宁 王 博 毛 宁

1.珠海城市职业技术学院机电工程学院，珠海 519090 2.吉林大学珠海学院机械与汽车工程系，珠海 519041 3. 北京理工大学宇航学院，北京 100081

机械臂作为机器人最为重要的执行部分，在机器操作终端起着不可忽视的作用，其执行性能、反应速度等更是研究人员关注的焦点。

机械臂是一种具有强耦合性的非线性集成式MIMO系统，易受到外界环境干扰的影响。因此，需要设计一种具有强稳定性的机械臂控制方法。通常，机械臂可简化为二自由度连杆机构。针对这一结构，在已公开的文献中，有很多控制方法，例如模型预测控制[1]，离散控制[2]，线性反馈控制[3]，滑模控制等[4-13]。早期对于机械臂的控制系统通常采用开环系统进行设计，但其效果不尽人意，控制精度低且抗扰动能力差[14]。文献[15]应用PID控制理论，所提出方法在控制器设计中对模型参数不作要求，但其鲁棒性不够好。文献[16]应用自适应控制理论，所设计系统能够有效降低系统的参数不确定性对机械臂控制的影响。文献[17]考虑了机械臂控制的全状态约束，基于神经网络控制理论，可保证系统响应始终处于全状态约束中。文献[18]应用自适应神经网络控制理论，但采用神经网络控制的方法对参数的设计选取有较大难度。文献[4-13,19]应用滑模变结构控制理论，由于滑模控制具有强鲁棒性的特点，可有效抵御系统内部与外界干扰；通过合理的趋近律设计，亦可实现有限时间收敛的特性；结合自适应算法，可避免繁琐的参数调试。

考虑到以机械臂作为被控对象的非线性与强耦合性的特点，本文基于终端滑动模态控制理论，设计了一种新型机械臂终端滑模控制方法。提出了一种具有有限时间收敛特性的鲁棒控制器，对所设计方法的有限时间收敛性进行了验证，并采用李雅普诺夫方法证明了其稳定性。通过对采用所设计控制方法的控制器与经典线性滑模控制器进行仿真对比，证明了所述方法能够实现在有限时间内控制两杆角速度与角加速度收敛至期望值。

1 机械臂结构模型与控制模型

机械臂结构模型可简化为图1所示的平面二自由度连杆模型。该机械臂系统由连根细杆组成，质量分别为m1和m2，长度分别为l1和l2。A和B两点可视为销钉，杆1可绕A点做圆周运动，杆2可绕B点做圆周运动。

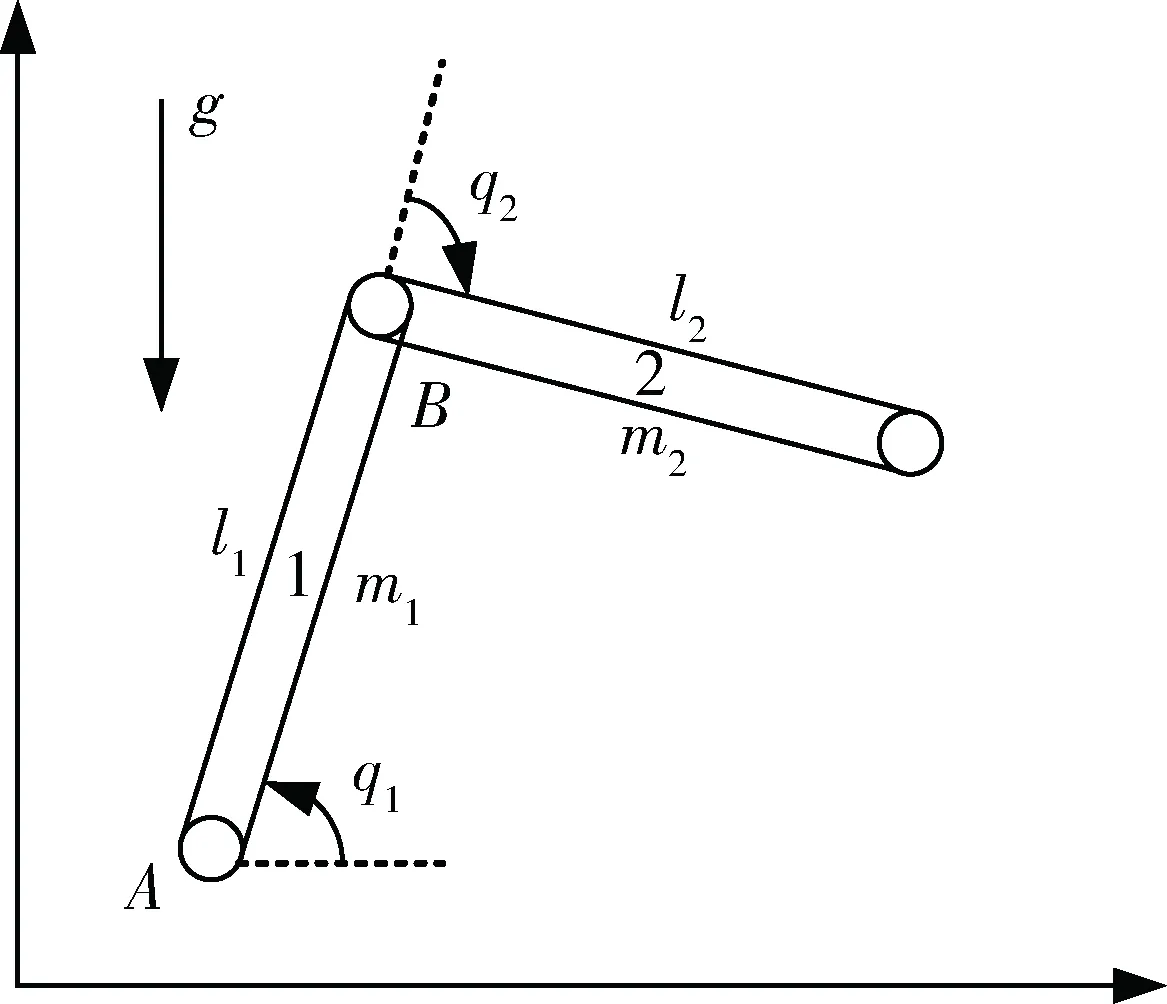
图1 二连杆机械臂平面模型

根据拉格朗日方程，可建立如下力学模型：

(1)

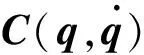
(2)

式中，g表示当地的重力加速度，J1和J2为绕其质心的转动惯量，满足以下关系：

(3)

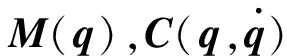
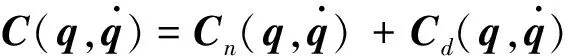
(4)

(5)

其中，

(6)

为系统的总不确定量。由文献[15]得，

(7)

其中，b0，b1和b2为正实数。

注1：由式(5)可以看出，该机械臂系统为一二阶系统，且杆1与杆2之间存在严重的控制耦合，解耦控制方法相当复杂。设计一种无需考虑解耦的非线性控制器，不失为一种高效的控制方法。

2 终端滑模控制器设计

定义期望角度向量为qd=[qd1,qd2]T,控制误差e1=q-qd, 则有

(8)

对于以上误差系统，定义终端切换函数

(9)

其中，α>0，β>0，γ∈(0,1)为切换函数的设计参数。趋近律可选取为

(10)

定理 1：考虑误差系统式(8), 切换函数式(9)以趋近律式(10)，式(11)所示滑模控制器可使系统式(8)在有限时间内渐进稳定且收敛至0。

(11)

式(9)～(11)中，sgn(·)为符号函数，其定义为

(12)

为进一步消除抖振，实际应用过程中，采用饱和函数代替符号函数。饱和函数的定义如下：

(13)

其中，δ>0为设计参数。不同的δ对应的饱和函数图像曲线如图2所示。

3 有限时间收敛性与稳定性分析

定理 2：考虑式(11)所示终端滑动模态鲁棒控制器，式(8)所示误差系统中状态量e1和e2可在有限时间内收敛至0；即系统式(4) 可在有限时间内收敛至预期。

图2 不同设计参数条件下的函数图像

证明：为分析该系统的有限时间收敛性与稳定性，有必要引入以下引理.

引理1[8]：对于C1型平滑系统f(x)∈，定义李雅普诺夫函数V(x)∈，如果该函数满足以下条件：

(14)

即式(14)不等号左侧半负定于实域空间，则有

(15)

式(14)和(15)中，β1∈+,β2∈+，η∈(0,1)。

选取如下李雅普诺夫函数：

(16)

(17)

可知在此控制器作用下，该系统稳定。

另外，

(18)

由引理1可知，系统会在有限时间收敛至滑模面。

(19)

式(19)中，Treach=[T1,T2]T∈+为双杆到达滑模面的之间，s0=[s10,s20]T为双杆滑模面的初值。

对切换函数式(9)应用引理1，显而易见的，切换函数式(9)可使控制误差e1及其导数e2在有限时间内收敛至0。

4 仿真实验与结果分析

为验证所述控制方法的鲁棒性，有限时间收敛性以及抖振抗性，将所述控制器与经典线性滑模控制器在相同初始条件、相同扰动条件下做仿真实验。仿真试验中，两杆的物理特性如表1所示。

表1 两杆的物理特性

期望的转角轨迹向量如下式所示：

(20)

扰动量选取为

(21)

作为对照，经典线性滑模控制器如下式所示：

(22)

s=e2+k1e1, sgn(s)=[sgn(s),sgn(s)]T

(23)

各控制器设计参数如表2所示

表2 各控制设计参数

仿真结果如图4～8所示。

图3 两杆期望角度与实际角度

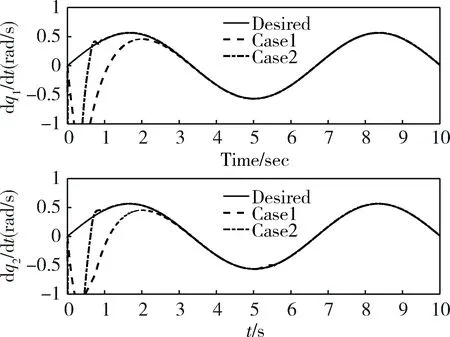
图4 两杆期望角速率与实际角速率

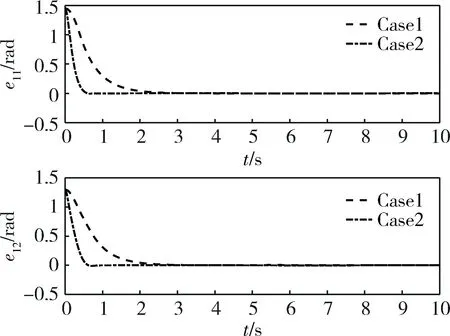
图5 两杆角度控制误差

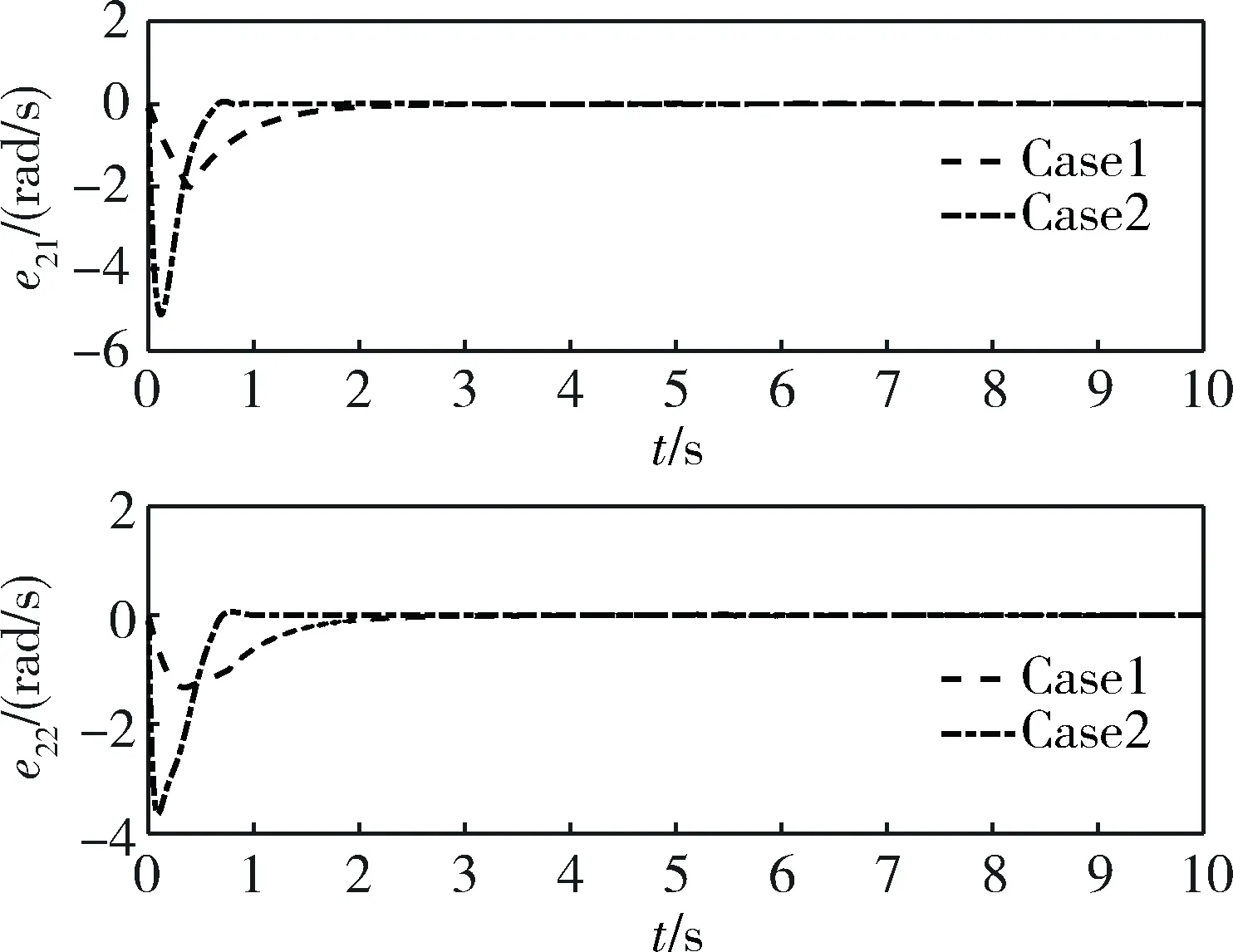
图6 两杆角速率控制误差

图7 两杆控制指令

由图3～7可知，在执行机构可以完全满足控制指令的条件下，本文所述控制器与线性滑模控制器均可满足控制需求。由图3可知，在2种控制器作用下，两杆角度均可收敛于期望角度，但本文所述控制器的收敛速度明显优于线性滑模控制器。如图4所示，在两杆角速率控制层面，本文所述控制器的收敛速度亦优于线性滑模控制器。图5和6分别显示了两杆角度与角速率层面，实际值与期望值之间的误差。由此二图得知，2种控制器均可使控制误差在一定时间之后收敛至0，但相对于线性滑模控制器，本文所述控制器收敛时间更短。

图7显示两杆的控制指令，在线性滑模控制器作用下，均会出现抖振现象，这对执行机构的高频特性要求很高，因而出现误差与错误的概率较高，不利于实际应用。相对于线性滑模控制器，本文所述控制器消除了抖振，易于实施。

为进一步探究设计参数对本文所述制导律的影响，分3种情况设计仿真实验，设计参数如表3所示。

表3 设计参数表

在两杆角度初值、扰动、误差和期望运动轨迹均与前文相同条件下，仿真结果如图8～12所示。

图8 两杆期望角度与实际角度

图9 两杆期望角速率与实际角速率

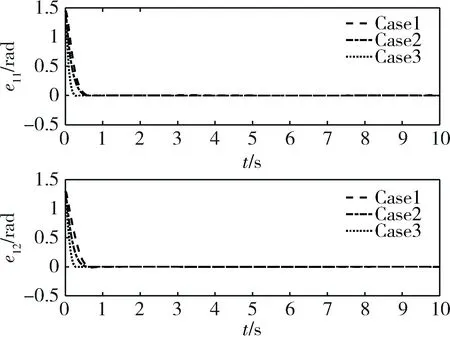
图10 两杆角度控制误差

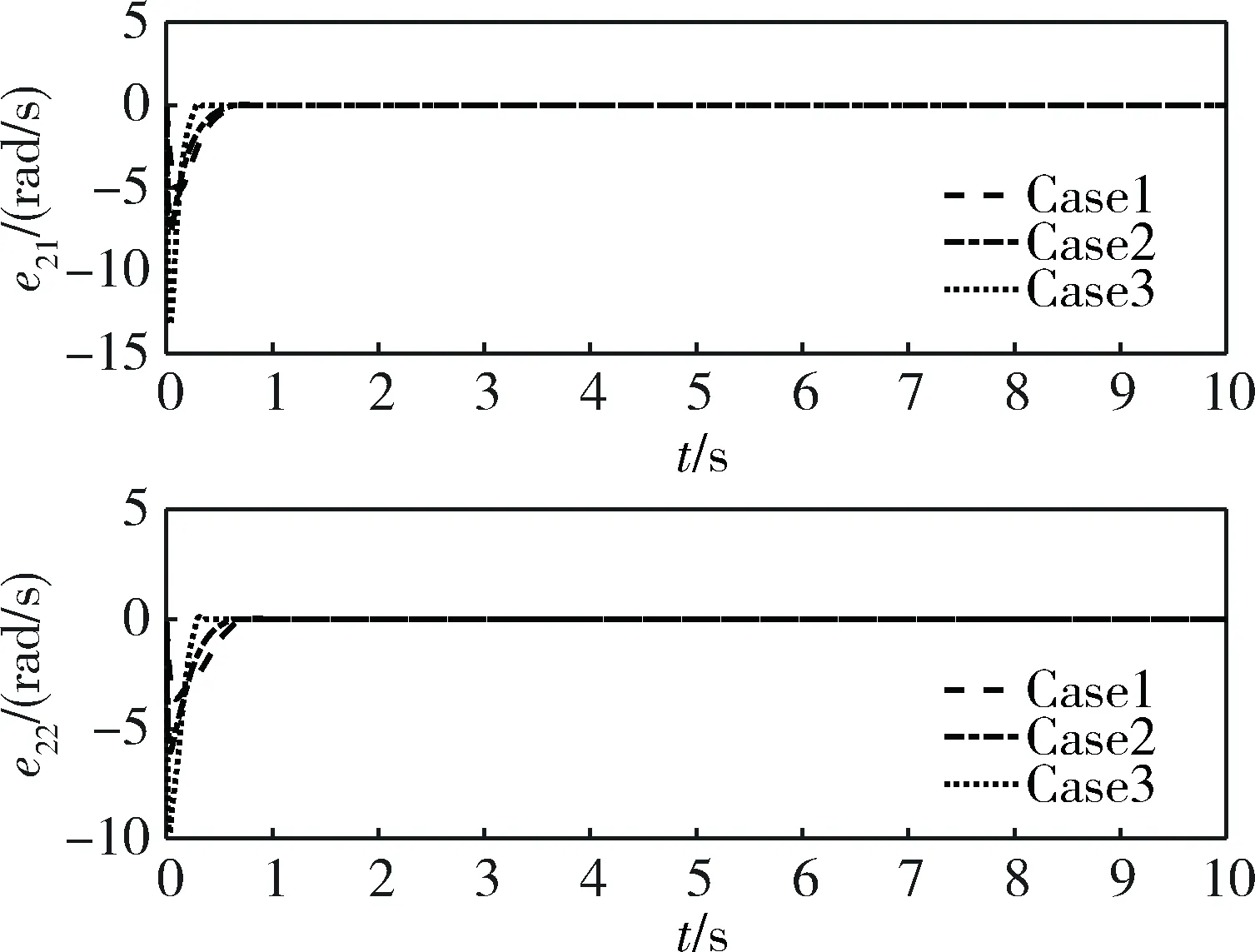
图11 两杆角速率控制误差

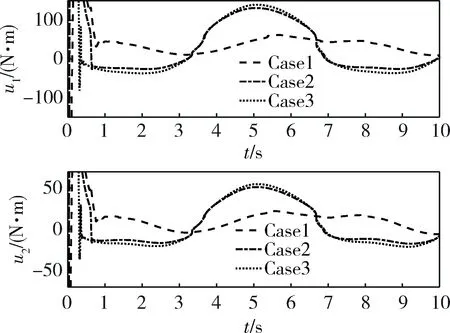
图12 两杆控制指令

由图8～11可知，在不同的设计参数下，两杆的角速度与角加速度均能迅速收敛至期望角速度与期望角加速度，角度控制误差与角速率控制误差均能迅速收敛至0，收敛时间小于1s，且抖振抑制效果良好，证明了所设计控制器的有限时间收敛性与鲁棒性。进一步通过对比可发现，当设计参数增大时，系统收敛速度亦随之增快。图12为两杆控制指令，从中可知，当设计参数增大时，控制指令波动幅度亦相对增大，从而产生更强有力的控制力。综上所述，在3种参数条件下，所述控制器均可完成控制任务，充分体现了所述控制器的参数普遍适应性。

5 结论

基于终端滑模控制理论，设计了一种可应用于普通机器人机械臂的控制器，该控制器具有以下优点：1)有效抑制了经典线性滑模控制中存在的控制指令抖振现象；2)适用于强耦合性与非线性系统，具有强鲁棒性；3)可控制系统于有限时间内收敛至期望状态。

参 考 文 献

[1] Poignet P and Gautier M. Nonlinear Model Predictive Control of a Robot Manipulator[J]. Proceedings of the 6thInternational Workshop on Advanced Motion Control, Nagoya, Japan, 2000:401-406.

[2] Chiacchio P, Pierrot F, Sciavicco L, et al. Robust Design of Independent Joint Controllers with Experimentation on a High-speed Parallel Robot[J]. IEEE Trans Ind Electron，2000， 40: 393-403.

[3] Kreutz K. On Manipulator Control by Exact Linearization[J]. IEEE Tans Autom Control，1989， 34: 763-767.

[4] Ferrara M and Magnani L. Motion Control of Rigid Robot Manipulators via First and Second Order Sliding Modes[J]. J Intell Robot Syst，2007， 48: 23-36.

[5] Wijesoma SW and Richards RJ. Robust Trajectory Following of Robots Using Computed Torque Structure with VSS[J]. Int J Control，1990， 52: 935-962.

[6] Liu M. Decentralized Control of Robot Manipulators: Nonlinear and Adaptive Approaches[J]. IEEE Tans Autom Control，1999， 44: 357-363.

[7] Feng Y, Yu X and Man Z. Non-singular Terminal Sliding Mode Control of Rigid Manipulators[J]. Automatica，2002， 28: 2159-2167.

[8] Yu S, Yu XH, Shirinzadeh B, et al. Continuous Finitetime Control for Robotic Manipulators with Terminal Sliding Mode[J]. Automatica，2005， 41: 1957-1964.

[9] Zhao D, Li C and Zhu Q. Low-pass-filter-based Position Synchronization Sliding Mode Control for Multiple Robotic Manipulator Systems[J]. Proc I Mech E, Part I: J Systems and Control Engineering，2011， 225: 1136-1148.

[10] Baek J, Jin M, Han S. A New Adaptive Sliding-Mode Control Scheme for Application to Robot Manipulators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6):3628-3637.

[11] Lee J, Chang P H, Jin M. Adaptive Integral Sliding Mode Control with Time-delay Estimation for Robot Manipulators[J]. IEEE Transactions on Industrial Electronics, 2017, (99):1-1.

[12] Gorji S, Yazdanpanah M J. A Robust Adaptive Sliding Mode Controller for Robot Manipulators[C]// Artificial Intelligence and Robotics. IEEE, 2017:170-176.

[13] Zhang F. High-speed Nonsingular Terminal Switched Sliding Mode Control of Robot Manipulators[J]. IEEE/CAA Journal of Automatica Sinica, 2017, PP(99):1-7.

[14] Youcef-Toumi K and Asada H. The Design of Open-loop Manipulator Arms With Decoupled and Configuration- invariant Inertia Tensors[C]// Proceedings of IEEE Conference on Robotics and Automation, 1986:2018-2026.

[15] Y. Su, D. Sun, L. Ren, et al. Integration of Saturated PI Synchronous Control and PD Feedback for Control of Parallel Manipulators[J]. IEEE Transactions on Robotics,2006，22(1): 202-207.

[16] Tomizuka M, Horowitz R, Model Reference Adaptive Control of Mechanical Manipulators[C]//Proceedings of the IFAC Symposium on Adaptive Systems in Control and Signal, 2014: 27-32.

[17] W. He, Y. Chen and Z. Yin, Adaptive Neural Network Control of an Uncertain Robot with Full-state Constraints[J]. IEEE Transactions on Cybernetics, 2016,46(3): 620-629.

[18] Sun C, He W, Hong J. Neural Network Control of a Flexible Robotic Manipulator Using the Lumped Spring-Mass Model[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2017, 47(8): 1863-1874.

[19] Islam S, P. X. Liu, Robust Sliding Mode Control for Robot Manipulators[J]. IEEE Transactions on Industrial Electronics, 2011,58(6): 2444-2453.

[20] He S, Lin D and Wang J. Chattering-free Adaptive Fast Convergent Terminal Sliding Mode Controllers for Position Tracking of Robotic Manipulators[J]. Proceedings of the Institution of Mechanical Engineers, Part C: J Mechanical Engineering Science, 2016; 230(4): 1-13.