采用自适应噪声估计的低轨卫星非差精密单点定位*

康国华 刘 瑶 金晨迪 杨炳辉 梁尔涛

1.南京航空航天大学航天学院微小卫星中心，南京210016 2.上海卫星工程研究所，上海201109

低轨卫星上的GNSS接收机处在一个高速运动状态，因此在定位过程中容易受到各种因素影响，导致定位产生系统性偏差。例如，GPS载波相位观测中的周跳、初始整周模糊度的确定误差、观测粗差等[1-2]。同时，低轨卫星在运行过程中，变轨、大气阻力或者姿态机动的干扰等都会给GNSS造成偏差项，从而导致定位精度下降，最终导致定轨精度不可靠。比如低轨卫星自主定轨，通常采用的大气模型是静态的，但实际上低轨大气环境变化明显，进而导致模型与实际情况不一致，构成模型误差。因此有文献提出对接收机输出信号的量测噪声进行实时估计[3]，修正测量误差从而提高定位精度。

对于这种随机的观测噪声，很难对每个时刻进行计算，只能通过长时间对观测数据的不断分析和统计来估计和修正观测噪声模型。基于上述分析，本文提出一种基于M-W组合观测值进行自适应估计观测噪声的方法。M-W组合观测值消除了电离层误差、对流层误差、卫星和接收机钟差影响等，剩下的主要有模糊度、观测噪声和相位硬件延迟影响[4-7]。M-W组合观测值中的模糊度是L1观测值和L2观测值的整周模糊度之差，为常整数，经过长时间的统计可以估计得到，接收机端相位硬件延迟影响可以通过星间单差消除，并采用IGS跟踪站组成的服务端观测网络提供的相应产品消除卫星端相位硬件延迟[8-9]。因此可以通过M-W组合观测值大致估计和统计观测噪声特性。

1 IGS精密星历辅助下的低轨卫星非差精密单点定位算法

非差精密单点定位算法是利用单台双频接收机的伪距和载波相位观测数据，结合精密的卫星轨道和卫星钟差产品，对影响定位的各种误差进行修正或者估计，利用载波相位的短波长特性，估计载波相位的模糊度，从而独立精确地确定该台接收机位置的方法[10]。

以GPS为例，其中以米为单位的伪距和载波相位观测方程可以表示为：

(1)

(2)

非差精密单点定位算法主要由3部分组成：观测数据和精密星历处理、参数估计以及模糊度固定。整个算法流程如图1所示。

整个算法，输入的数据源有2个：1)接收机收到的双频伪距和载波相位数据，2)通过卫星遥测通道上注的IGS精密星历。通过对IGS精密星历产品的分析可得，要得到实时的定位数据，只能采用超快预报星历，该星历比接广播星历精度高，略低于事后精密星历。广播星历提供的卫星轨道精度大概1m左右，而超快预报精密星历提供的轨道精度约为5cm，可大大提高定位精度。对于实时精密单点定位，需要地面测控支持，把当天需要使用的超快预报星历提前注入到星上。

考虑到星上计算能力有限，参数估计方法采用递推最小二乘法来估计参数，估计的参数主要有定位的位置，各颗卫星的模糊度和接收机钟差。

对于各颗卫星的模糊度确定，主要采用最小二乘模糊度降相关平差(Least Squares Ambiguity Decorrelation Adjustment, LAMBDA)算法，通过对原始模糊度参数进行整数变换，降低模糊度参数之间的相关性，从而达到缩小搜索范围的目的[10-12]。

2 非差精密单点定位中的噪声统计分析

在普遍的非差精密单点定位算法中，观测噪声R阵一般采取的是固定阵，但实际情况表明由于受接收机所处环境影响，接收机输出观测噪声的估计并不是定值。以诺瓦泰OEM617型号双频接收机为例。使用该型号接收机采集2017年3月12日12：00至17:00五个小时的静态数据，分析接收机输出的L1伪距和载波相位的标准差如图2和图3：

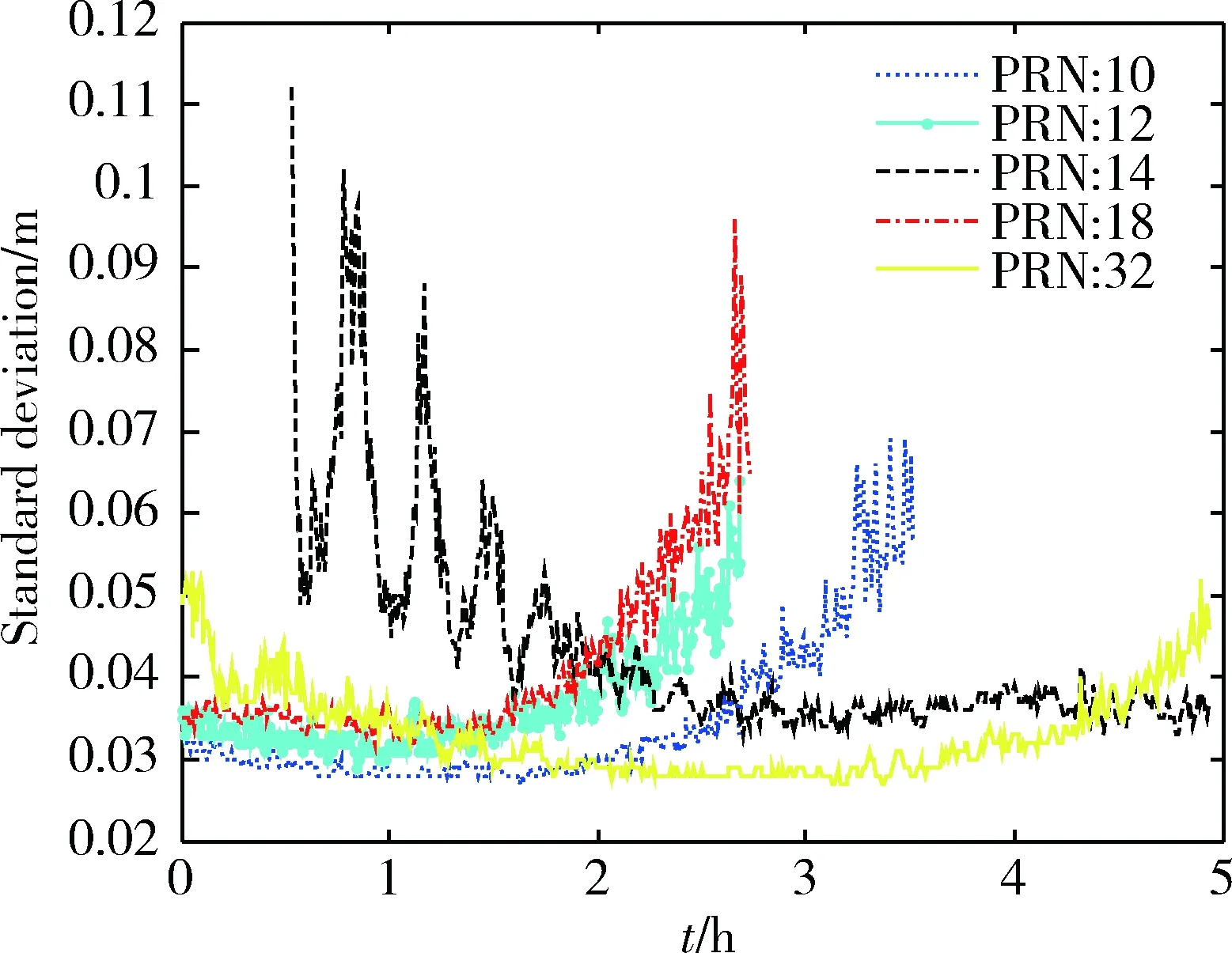
图2 L1伪距标准差

图3 L1载波相位标准差

图2和3中横坐标为接收机接收数据的时间，单位为小时，纵坐标为标准差，伪距标准差单位为米，载波相位标准差单位为周。图中分别画出了卫星编号(PRN)为10、12、14、18和32号的伪距和载波相位标准差。

由图可见观测噪声是时变的，不同卫星噪声特性不同。对于定位精度要求达到分米级甚至厘米级的高精度定位，如果采用的R阵是定常阵，将会严重影响结果的精度。

3 观测噪声对定位误差影响分析

在非差精密单点定位算法中，对于估计定位结果主要利用递推最小二乘算法，求解定位结果和大致模糊度，其中方程式如下[13]：

yk=Hkx+vk

(3)

式中，vk是测量噪声，且认为每一个测量噪声都是相互独立的；yk是新获得的测量值；Hk是测量矩阵。

递推估计值为：

(4)

上一步估计值；估计误差均值可以表示为：

(5)

式中，Kk为增益矩阵，由式(4)和式(5)可知每一次的测量噪声都会计入最后的估计误差中。

根据递推得到估计误差协方差矩阵Pk为：

(6)

(7)

由图1可知，最小二乘估计中的协方差矩阵Pk将继续带入LAMBDA算法中进行模糊度固定的求解，由此将测量噪声误差也引入整周模糊度估计误差中。

因此需要对伪距和载波相位组合观测值测量噪声进行准确估计，避免导致定位解算误差的增大甚至发散。由于不同观测历元模型下，误差具有不同的特性，而如何求解噪声的准确估计是一个难点。

4 观测噪声的误差估计

在非差精密单点定位中，常使用M-W组合确定周跳和粗差。因为M-W组合在一定程度上消除了大部分误差项，余下的主要是模糊度线性组合值、相位硬件延迟和观测噪声。M-W组合观测值的表示方程为：

(8)

式中，NΔ=N1-N2也叫做宽巷模糊度，是L1和L2频率的载波相位模糊度之差，具有整周特性，λΔ是宽巷模糊度波长，ε是观测噪声以及相位硬件延迟。相位硬件延迟可以利用IGS跟踪站组成的服务端观测网络提供的相应产品和星间单差予以消除。在不考虑周跳的情况下，通过多历元平滑可以得到宽巷模糊度，再消除相位硬件延迟即可得到大致的观测噪声。然而得到的观测噪声协方差值仅能代表M-W组合观测值的协方差，不能完全替代去电离层组合的观测噪声协方差值。为了获得去电离层组合的观测噪声，可以通过推导M-W组合观测值和去电离层组合之间的关系得到。去电离层组合观测值可以表示为：

(9)

则伪距和载波相位观测噪声可以表示为：

(10)

而M-W组合观测值的观测噪声可以表示为：

(11)

从上述表达式中，假设εL1和εL2观测噪声相同且εP1和εP2观测噪声相同，则可以得到:

(12)

在实际调试过程中，从得到的伪距和载波相位观测值的标准差的图中(图2和3)，伪距的观测噪声大概为载波相位观测噪声的10倍左右，具体和接收机性能等其他因素有关，因此可以得到M-W组合的观测噪声大概为：

εMW=εL-εP≈9εL

(13)

M-W组合观测值的观测噪声约为去电离层组合中载波相位观测值的观测噪声的9倍。

5 自适应最小二乘估计算法

在最小二乘法参数估计时，tk时刻测量噪声序列的方差阵Rk通常会采用定常经验值，即采取多组Rk值经过多次测试得到一个相对较好的结果。在实际应用过程中，在一个未知环境下要得到高精度的实时定位结果，单使用定常经验值的Rk阵无法达到要求精度，因此采用对当前观测值的噪声进行统计的自适应算法计算得到Rk阵[14-16]。得到的Rk阵和接收机接收的观测值有关，且随环境变化和接收机接收性能变化而变化。

已知测量误差可以表示为：

(14)

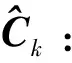
(15)

或写成迭代形式：

(16)

可以得到观测噪声方差阵的估计：

(17)

6 自适应算法验证及分析

对算法进行验证的数据采集于2017年3月15日12时至17时，接收机天线固定在屋顶，四周开阔，无遮挡，接收信号环境良好。采集5个小时的静态数据，实时解算周期是30s(由于应用于低轨卫星，考虑到地面注入参数的稀疏性和星载计算机的处理能力，采用30s解算周期)。

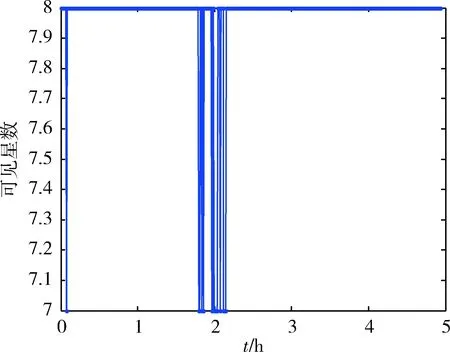
图4 观测期间可见GPS卫星数图

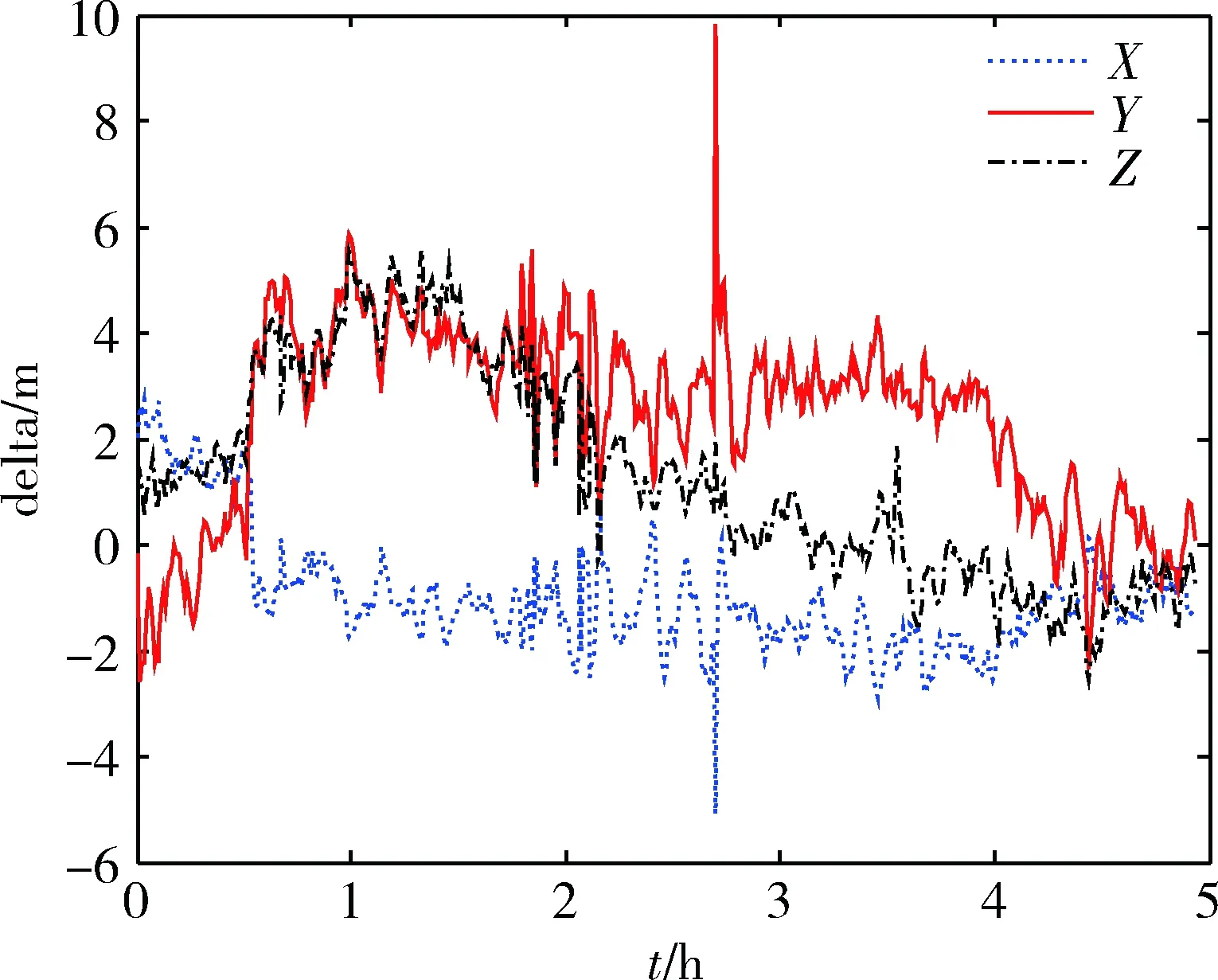
图5 接收机定位精度

为了验证本文提出的自适应噪声估计算法的有效性，对同一数据文件用不同定位算法进行仿真，对比定位结果。首先是观测噪声估计取定常的算法，根据接收机性能和多次测试得到的经验值，伪距观测噪声取0.2m，载波相位的观测噪声取0.02m。实时仿真计算获得的定位误差如图6所示，这里定义误差是算法计算结果与接收机本身输出的定位结果均值的差值。

图6 定位误差

统计分析表明，在噪声估计定常情况下，非差精密单点定位定位误差在84坐标系X，Y，Z方向上分别为1.7m，0.84m和0.25m。

如采用自适应噪声调节，仿真得到定位误差如图7所示。

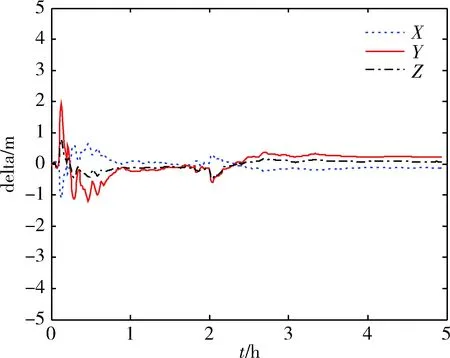
图7 定位误差

经统计，R阵自适应调整后，非差精密单点定位X，Y，Z方向上误差分别为0.20m，0.37m和0.16m。相比于定R算法，X轴误差降低了一个数量级，Y轴和Z轴的精度提高了1倍，收敛速度也从原来的2h提高到1h，收敛更趋于稳定。

除了上述测试外，在不同时段、不同地点的仿真结果均一致。本仿真验证采用的是地面静态数据，与实际低轨卫星运行环境有所不同，但采用的方法基本一致。对于低轨卫星和地面验证实现的非差精密单点定位中，最大的区别就是低轨卫星和地面测站所处的环境不相同，所受环境影响导致的测量误差也有所不同。比如说低轨卫星接收到的GPS信号不受对流层延迟影响，但受到电离层延迟的影响更加复杂。由于低轨卫星的轨道高度一般高于电离层峰值高度，地面电离层延迟的修正模型仅在一定程度上适用于低轨卫星。本身去电离层组合仅消去了一阶电离层延迟的影响，而太空中，电离层延迟的影响可以通过接收机相位的硬件延迟表现出，因此地面验证的时候把这一类归为接收机的相位硬件延迟误差[17]。

7 结论

在非差精密单点定位算法中，对观测噪声进行评估统计，即将R阵实时自适应调整，同时对观测噪声模型进行修正，可在很大程度上减弱系统噪声误差的影响，使得定位结果在受到外界干扰后重新快速收敛，并将定位精度提高一个量级，收敛时间能够从2～3h减少到1h。本文根据接收机性能和线性组合特性估计观测噪声，克服了观测噪声难以评估和统计的问题，有效提高了定位精度和收敛时间。

参 考 文 献

[1] 李征航, 黄劲松. GPS测量与数据处理[M].武汉：武汉大学出版社, 2010:131-162.

[2] Bertiger W, Desai S D, Haines B, et al. Single Receiver Phase Ambiguity Resolution with GPS Data[J]. Journal of Geodesy, 2010, 84(5):327-337.

[3] 王甫红，龚学文，徐其超，张蔚.时变大气模型应用于低轨卫星自主定轨[J].测绘科学技术学报, 2013, 30(3): 219-224(Wang Fuhong, Gong Xuewen, Xu Qichao, Zhang Wei. Time-varying Atmosphere Model and Its Application to LEO Satellite Autonomous Orbit Determination [J]. Journal of Geomatics Science and Technology, 2013, 30(3): 219-224.)

[4] Cai C S, Gao Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning [J]. GPS Solut, 2013, 17:223-236.

[5] 李东霞, 宋馥含, 刘瑞华. 北斗系统整周模糊度及周跳的确定算法[J]. 航天控制, 2017, 35(1): 66-70. (Li Dongxia, Song Fuhan, Liu Ruihua. The Determination Algorithms of Integer Ambiguity and Cycle Slip in BDS[J]. Aerospace Control. 2017, 35(1): 66-70.)

[6] Zhang B., Teunissen P.J.G., Odijk D., A Novel Un-differenced PPP-RTK Concept[J]. Journal of Navigation, 2011, 64(S1).

[7] 李晓宇, 董绪荣, 帅玮祎, 刘烜塨. 基于超快精密星历的空间信号完好性监测算法[J]. 2017, 35(1):48-53. (Li Xiaoyu, Dong Xurong, Shuai Weiyi, Liu Xuangong. Algorithm of Signal in Space Integerity Monitoring Based on Ultra Rapid Precise Ephemeris[J]. Aerospace Control. 2017, 35(1): 48-53.)

[8] 李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉:武汉大学, 2013. (Li Xingxing. Rapid Ambiguity Resolution in GNSS Precise Point Positioning [D]. Wuhan: Wuhan University, 2013.)

[9] 郑艳丽. GPS非差精密单点定位模糊度固定理论与方法研究[D]. 武汉: 武汉大学, 2013.(Zheng Yanli. Research on Integer Ambiguity Resolution in GPS Precise Point Positioning [D]. Wuhan: Wuhan University, 2013.)

[10] 苌永娜, 张海, 李玉洁, 杨静. 基于R阵动态估计的自适应滤波算法[J]. 电光与控制, 2012, 19(3): 26-31. (Chang Yongna, Zhang hai, Li Yujie, Yang Jing. An Adaptive Kalman Filtering Algorithm Based on the Dynamic Estimation of Measurement Noises [J]. Electronics Optics and Control, 2012, 19(3): 26-31.)

[11] Seepersad G, Bisnath S. Reduction of PPP Convergence Period Through Pseudo-range Multipath and Noise Mitigation[J]. GPS Solutions, 2015, 19(3): 369-379.

[12] 李征航, 张小红. 卫星导航定位新技术高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009: 1-49.

[13] Dan Simon. 最优状态估计-卡尔曼，及非线性滤波[M]. 张勇刚, 李宁, 奔粤阳 译. 北京:国防工业出版社, 2015: 58-63.

[14] 杨元喜, 张双成. 导航解算中的系统误差及其协方差矩阵拟合[J]. 测绘学报, 2004, 33(3): 189-194. (Yang Yuanxi, Zhang Shuangcheng. Fittings of Systematic Errors and Covariance Matrices in Navigation [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 189-194.)

[15] 袁书明, 杨晓东, 程建华. 导航系统应用数学分析方法[M]. 北京: 国防工业出版社, 2013: 197-202.

[16] 杨元喜, 张双成. 导航解算中的系统误差及其协方差矩阵拟合[J]. 测绘学报, 2004, 33(3): 189-194. (Yang Yuanxi, Zhang Shuangcheng. Fittings of Systematic Errors and Covariance Matrices in Navigation [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 189-194.)

[17] 钟嘉豪. 基于低轨卫星TEC数据的顶部电离层变化特性研究[D]. 合肥: 中国科学技术大学, 2017. (Zhong Jiahao. Investigation on the Variations of the Topside Ionosphere Using Low Earth Orbit Satellite-based TEC[D]. Hefei: University of Science and Technology of China, 2017.)