基于极限学习机的非平稳下击暴流风速预测

钟 旺,李春祥

(上海大学土木工程系,上海200444)

非平稳脉动风速是一种具有非线性和非平稳性的特殊序列信号,其中的非平稳下击暴流风速是强非平稳过程.尽管极限学习机(extreme learning machine,ELM)能够较好地拟合风速的非线性部分,但风速非平稳部分将对预测效果造成较大的影响,因此降低风速非平稳性就显得尤为重要[1].降低非平稳性的主要方法有小波变换和经验模态分解(empirical mode decomposition,EMD).EMD将复杂非平稳性信号分解成不同频率段的信号,从而降低序列的非平稳性;集合经验模态分解(ensemble empirical mode decomposition,EEMD)将白噪声序列加入到原始序列,这样尽可能地得到数据信号的真实形态,然后再对数据信号进行EMD分解;快速集合经验模态分解(fast ensemble EMD,FEEMD)是EEMD的快速实现形式.

目前,预测模型主要有时间序列模型、人工神经网络(artif i cial neural network,ANN)模型、支持向量机(support vector machine,SVM)模型和最近的ELM.ELM是Huang等[2-3]于2004年提出的一种性能优良的新型单隐层前馈神经网络(single-hidden layer feed forward neural networks,SLFNs),其基本思想是训练前设置合适的隐层节点数,在执行过程中只需要输入权值和为隐层偏置随机赋值,整个过程无需迭代,一次性产生唯一的最优解.与ANN相比,ELM显著提高了网络的泛化能力和学习速度,具有强非线性拟合能力.因此,当前国内外研究人员非常重视极限学习机的发展.鉴于ELM优势,本工作试图建立基于ELM的非平稳下击暴流风速预测算法.将EMD和FEEMD与基于粒子群优化(particle swarm optimization,PSO)的最小二乘支持向量机(least squares support vector machines,LSSVM)进行混合,形成EMD-PSO-LSSVM和FEEMD-PSO-LSSVM混合模型算法.

1 非平稳下击暴流脉动风速的分解

1.1 经验模态分解法

EMD是Huang等[4]于1998年提出的数据处理方法,将非平稳信号按不同尺度的波动或趋势逐级分解成若干个固有模态分量(intrinsic mode function,IMF).每个IMF需满足2个条件:①数据集的极值点个数与穿0点个数相等或至多相差一个;②在任一点,由所有极大值点所形成包络和由所有极小值点所形成包络的均值等于0.

设U(t)为待分解的非平稳风速样本,先找出其所有极大、极小值,接着使用3次样条函数拟合出上、下极值包络线,计算出上、下包络线的平均值m1(t).于是,去除均值后的第1分量为

第1次筛分所得分量h1(t)通常并不满足IMF的要求,故将h1(t)作为新的待筛分序列,再进行k次筛分,直到h1k(t)满足IMF的要求为止.于是,把h1k(t)当作IMF1,记为c1(t)=h1k(t).第1个IMF1[c1(t)]包含了非平稳风速U(t)的最短周期分量,将c1(t)从U(t)中分离后的余量为

但是,r1(t)仍然包含较长周期分量,再将r1(t)作为新的待筛分序列,筛分得第2个IMF2[c2(t)];继续进行这样的筛分过程,直到余量变得很小为止.最终余量为

那么,非平稳风速U(t)被分解成IMFs之和再加上最终余量:

1.2 快速集合经验模态分解法

EMD常常出现模态混叠现象,造成IMF物理意义上的缺失.为此,Huang[5]通过将白噪声加入待分解信号提出了EEMD.当将在整个时-频空间分布一致的零均值白噪声加到待分解信号时,不同时间尺度信号将自动分布到合适的参考尺度上,经多次平均噪声将相互抵消,集成均值结果.与EMD相同,EEMD将非平稳风速U(t)分解成IMFs之和再加上最终余量rn(t),即式(4).而FEEMD则是EEMD的快速实现方式,其原理与EEMD相同[6].

2 下击暴流脉动风速智能预测模型

2.1 基于粒子群优化最小二乘SVM的风速预测

Suykens[7]用误差的二次平方来代替SVM的不敏感损失函数,将不等式约束转变为等式约束,进而将求解二次规划问题转化成求解如下的线性方程组,即形成LSSVM:

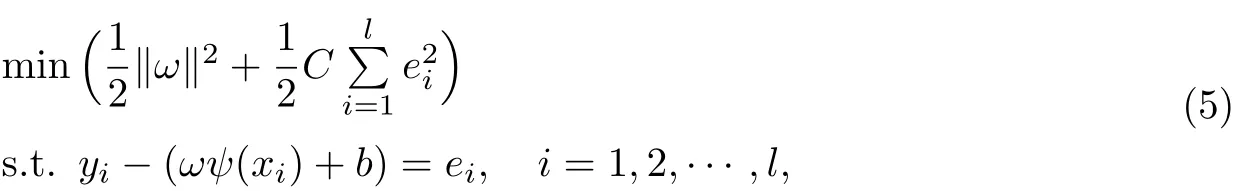
式中,ω为权向量,b为偏置项,C为惩罚参数,ei∈R为误差,ei∈Rl×l为误差向量.为解决式(5)的优化问题,构造Lagrange函数:

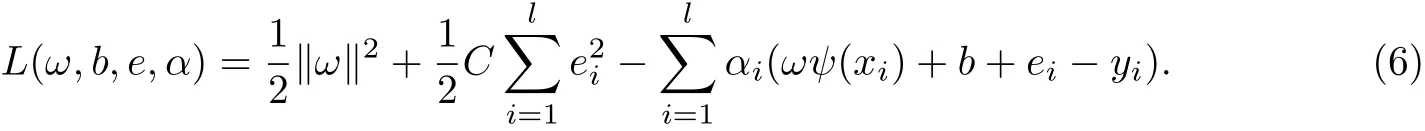
对式(6)求偏导,并根据最优化理论中的KKT(Karush-Kuhn-Tucher)条件,得到如下方程组:

设 α =(α1,α2,···,αl)T,Q=(1,1,···,1)T,Y=(Y1,Y2,···,Yl)T,I 为单位矩阵. 联立求解方程组,消去ω和ei,则式(7)的解为

于是得到LSSVM的回归模型:

式中,K为核函数矩阵,其元素k(xi,xj)=ψ(xi)ψ(xj).本工作采用径向基(radial basis function,RBF)核函数,其表达式为

采用PSO算法对LSSVM中的核参数进行优化,形成基于粒子群优化的最小二乘SVM(PSO-LSSVM).

2.2 基于极限学习机的风速预测

ELM是一种快速的单隐层前馈神经网络训练算法[8].针对训练数据样本(x,t),隐含层节点数为L、激发函数为g(x)的ELM模型输出函数表达式为

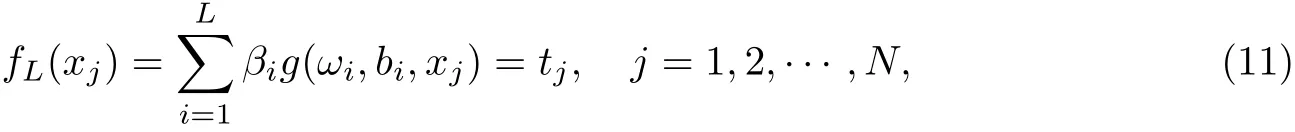
式中,β =[βi1,βi2,···,βin]T为第 i隐层节点和输出节点间的连接权向量;ω =[ωi1,ωi2,···,ωin]T为连接第i隐层节点和输入节点的权重;bi为第i隐层节点的偏置;tj为第j个节点的输出值,ωixj为ωi和xj的内积.激发函数g(x)可以为Sigmoid,Sine或Hardlim等.

式(11)的矩阵表达式可表示为

式中,H=式中,H为隐层输出矩阵,其第i列表示为第i个隐层节点对应于输入x1,x2,···,xN的第i个隐层神经元的输出向量.

运用式(12),将数据样本集映射到隐含层的特征空间中.设E(W)为ELM网络输出值与实际值之间的误差平方和,问题的求解转化为求解最优权值W=(ω,b,β),使E(W)最小:

式中,εj=(εj1,εj2,···,εjm)T是第 j 个样本的误差.

当激发函数无限可微时,并不需要将网络参数全部进行调整,输入连接权值ω和隐含层节点偏置b在训练时可以随机选择.当隐含层节点数目足够多时,输入权随机取值,ELM可逼近任何连续函数.为使ELM具有较好的泛化能力,通常使L≪N.因此,连接隐层和输出节点的权值β可通过求解线性方程组Hβ=T的最小二乘解获得,其解为式中,H+为输出矩阵H的Moore-Penrose广义逆矩阵.

至此,基于ELM风速预测算法的步骤如下:

(1)随机赋值隐层节点和输入节点的权重ωi、隐层节点偏置bi(i=1,2,···,L);

(2)计算隐含层输出矩阵H=

(3)通过求解线性方程组(13)的最小二乘解计算输出层权重β.

图1给出了基于ELM和PSO-LSSVM的非平稳下击暴流风速预测算法流程.

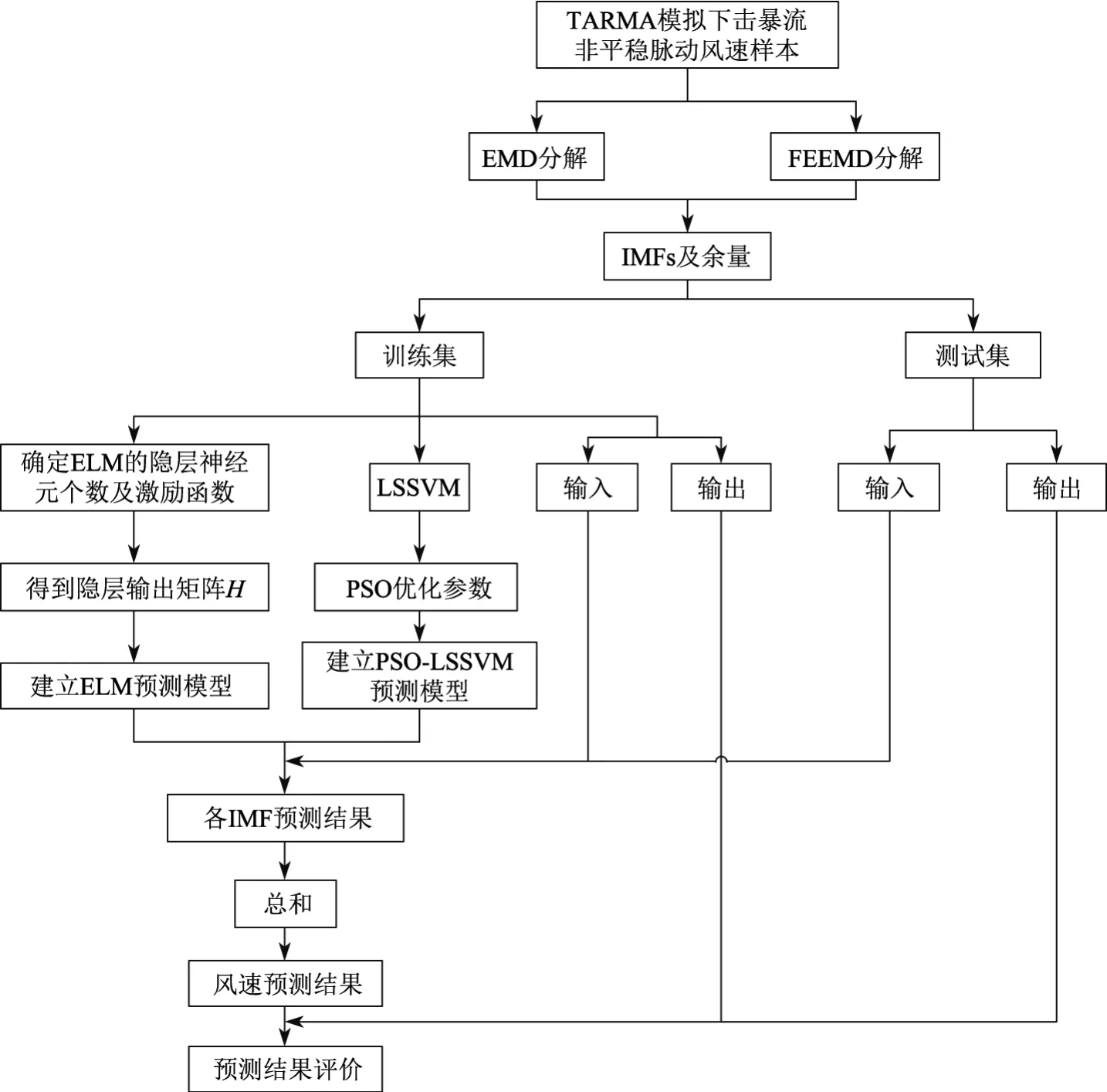
图1 基于ELM和PSO-LSSVM的非平稳下击暴流风速预测算法流程Fig.1 Flowchart of ELM and PSO-LSSVM based on non-stationary downburst wind velocity prediction algorithms

3 风速智能预测算法的数值验证

3.1 非平稳下击暴流风速模拟

下击暴流为雷暴天气中强烈的下沉气流猛烈撞击地面,并由撞击点向四周沿地表传播的极具突发性和破坏性的一种高强风[9].运用时变自回归滑动平均模型(auto-regressive moving average model,TARMA)[10-12]模拟m维非平稳脉动风速的表达式为

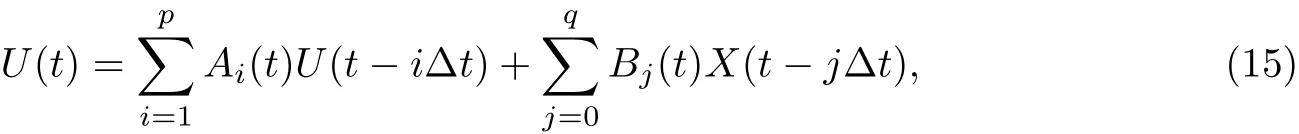
式中,U(t)为非平稳随机过程向量,Ai(t)为回归系数矩阵,B(t)为时变滑动回归系数矩阵,p为自回归阶数,q为滑动回归阶数,X(t)是方差为1、正态分布的白噪声序列.

TARMA模型p=4,q=1,模拟点位于沿下击暴流移动方向且距离下击暴流雷暴中心3 500 m处.下击暴流的平均风速模型采用Oseguera和Bowles模型;竖向分布模型采用Vicroy模型,其中竖向分布风速中最大风速Vmax=80 m/s,所处高度Zmax=67 m;风速场中某高度处径向最大风速Vr,max=47 m/s,与下击暴流中心水平距离rmax=1000 m,径向长度比例系数Rr=700 m.雷暴强度随时间变化的函数为

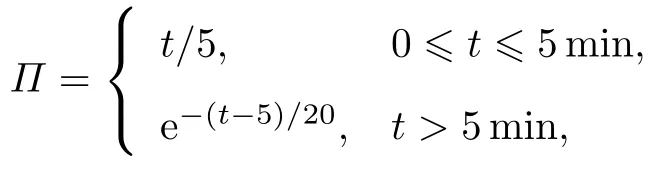
下击暴流平移速度V0=8 m/s.当运用TARMA模型模拟时,上限截止频率为2πrad,N=211,Δω =同时,考虑下击暴流自身移动,模拟时间间隔Δt=0.5 s,模拟时长为1 000 s,共2 000个样本点.图2给出了运用TARMA模型模拟出的高度在20 m处的非平稳下击暴流脉动风速结果.

图2 运用TARMA模型模拟出的高度在20 m处的非平稳下击暴流脉动风速Fig.2 Non-stationary downburst f l uctuating wind velocity at 20 m height simulated by TARMA

3.2 预测算法数值验证

ELM模型的隐层节点L=20,激发函数为Sigmoid;PSO-LSSVM采用RBF核函数,模型核参数2σ2∈[0.01,100],q=3,惩罚参数c∈[0.1,1 000].将非平稳下击暴流脉动风速的分解模型和预测模型两两组合,产生组合预测模型:EMD-ELM,EMD-PSO-LSSVM,FEEMD-ELM和FEEMD-PSO-LSSVM.

运用TARMA模型模拟出的1 000 s非平稳下击暴流脉动风速样本是以0.5 s为时间单位,则样本中有2 000个风速点.取前1 000个风速点(500 s)构成训练集,后1 000个风速点(500 s)作为测试集.对1 000 s非平稳下击暴流脉动风速分别进行EMD和FEEMD分解,得到如图3所示的结果,其中的Signal为原始(模拟)非平稳风速,imf 1～8为分解后的固有模态函数,res为筛分后余量很小的剩余分量.在FEEMD分解时,白噪声方差α取为0.25,噪声组的数值取为100.当α取为0,噪声组数值取为1时,FEEMD就转化为EMD.

将IMFs进行相空间重构,选取时间延迟τ=1,嵌入维数m=10,于是产生的训练集为990个10维向量,测试集为1 000个10维向量.使用上述4种组合预测模型对该非平稳下击暴流脉动风速样本进行预测,将各个IMF分量的预测结果进行叠加,得到非平稳下击暴流脉动风速的预测结果.

图3 非平稳下击暴流脉动风速的分解Fig.3 Decompositions of the non-stationary downburst f l uctuating wind velocity

图4 基于ELM和PSO-LSSVM的预测风速与模拟风速比较Fig.4 Comparisons of predicted wind velocity using ELM and PSO-LSSVM with the simulated wind velocity

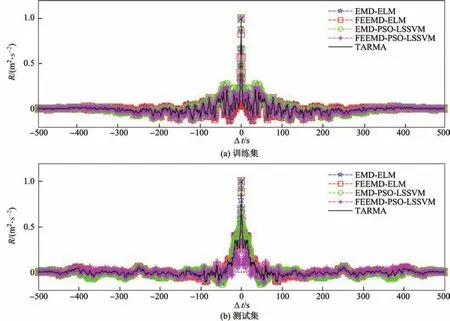
图5 基于ELM和PSO-LSSVM预测风速与模拟风速自相关函数的对比Fig.5 Auto-correlation function comparisons of predicted wind velocity using ELM and PSO-LSSVM with the simulated wind velocity

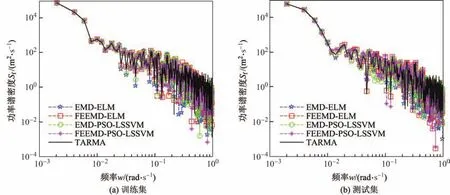
图6 基于ELM和PSO-LSSVM预测风速与模拟风速功率谱函数的对比Fig.6 Power spectral function comparisons of predicted wind velocity using ELM and PSOLSSVM with the simulated wind velocity

运用EMD-ELM,EMD-PSO-LSSVM,FEEMD-ELM和FEEMD-PSO-LSSVM预测模型对非平稳下击暴流脉动风速进行预测.图4～6分别给出了预测与模拟的非平稳下击暴流风速、自相关函数以及功率谱函数.由图4～6可知,在非平稳风速、自相关函数和功率谱3个方面,4种预测模型的预测结果均与TARMA模型的模拟值(原始值)较好地吻合,其中FEEMD-ELM的吻合度最高.

4 风速智能预测算法的预测性能

根据训练集和测试集,分别计算了预测风速与模拟风速的平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)和相关系数(R),以比较这4种组合预测模型的预测精度.表1给出了4种预测模型对训练集和测试(预测)集的预测性能指标.由表1可以看出,无论是对训练集还是测试集,使用FEEMD分解的各IMF分量来进行预测,其精度均高于EMD;采用ELM预测模型进行预测的效果优于PSO-LSSVM.显然,采用FEEMD-ELM的预测精度是4种预测模型中最好的.综上所述,EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高精度算法.

表1 训练集和测试集的预测性能指标Table 1 Prediction performance indexes for training and testing sets

表1中,平均误差为目标值(原始样本数据),^yn为预测值,N为预测样本数;均方根误差RMSE=相关系数R=

5 风速智能预测算法的计算速度

通过比较计算时间可以发现,运用EMD对非平稳下击暴流脉动风速进行分解的耗时较短;由于EEMD需要向信号中添加白噪声平滑脉冲干扰,因此耗时相对较长;FEEMD则有效改善了EEMD耗时较长的缺点,显著提高了EEMD的分解速度.不过,相对于预测的耗时,脉动风速分解的耗时是可以忽略的.

更为重要的是,ELM预测模型的计算耗时约为28 s,而PSO-LSSVM预测模型的计算耗时则约为821 s,PSO-LSSVM耗时约为ELM的30倍.可见,EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高速算法.

6 结束语

经训练集和测试集非平稳下击暴流脉动风速时间序列、自相关函数和功率谱模拟值与预测值以及预测性能指标的比较后发现,对于EMD-ELM和FEEMD-ELM算法,训练集和测试集的预测精度均高于EMD-PSO-LSSVM和FEEMD-PSO-LSSVM算法.相对于PSO-LSSVM算法,ELM预测算法的参数选取更容易、简单,在训练过程中不需要调整输入权值和偏置,训练速度显著提高;而且,该算法只需设定合适的隐层节点和激发函数便可以获得唯一的最优解,故EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高精度、高计算速度的算法,其中FEEMD-ELM是更为优秀的算法.

[1]张翌晖,王贺,胡志坚.基于集合经验模态分解和改进极限学习机的短期风速组合预测[J].电力系统保护与控制,2014,42(10):29-34.

[2]HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]//Proceedings of International Joint Conference on Neural Networks.2004:985-990.

[3]WANG D,HUANG G B.Protein sequence classif i cation using extreme learning machine[C]//Proceedings of International Joint Conference on Neural Networks.2005:1406-1411.

[4]HUANG N E,SHEN Z,LONG S R.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc Roy Soc,1998,454(17):903-905.

[5]WU Z,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[6]WANG Y H,YEH C H.On the computational complexity of the empirical mode decomposition algorithm[J].Physica A,2014,1:159-167.

[7]SUYKENS J A K,VAN DEWALLE J.Least squares support vector machine classif i ers[J].Neural Processing Letters,1999,9:293-300.

[8]HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:theory and application[J].Neurocomputing,2006,70(1/2/3):489-501.

[9]李锦华,吴春鹏,陈水生.下击暴流非平稳脉动风速数值模拟[J].振动与冲击,2014,33(14):54-60.

[10]LI J H,LI C X,HE L,et al.Extended modulating functions for simulation of wind velocities with weak and strong nonstationarity[J].Renewable Energy,2015,5:384-397.

[11]何亮.基于时变ARMA的非平稳风速模拟与预测[D].上海:上海大学,2015.

[12]李春祥,迟恩楠,何亮,等.基于时变ARMA和EMD-PSO-LSSVM算法的非平稳下击暴流风速预测[J].振动与冲击,2016,35(17):33-38.