环境约束下长江经济带投入效率的时空差异

王琳玉,于丽英

(上海大学管理学院,上海200444)

目前,中国经济由投入型增长转向效率型增长,如果想进一步推进供给侧结构改革,那么就需要通过产业调整、创新来提高投入效率.由于经济发展受制于技术进步和要素投入,因此技术进步与要素投入的效率变化是反映投入效率的2个主要指标.目前,关于投入效率的测算方法主要有数据包络分析(data envelopment analysis,DEA)法、Malmquist指数法和Malmquist-Luenberger(ML)指数法[1].由于前2种方法只考虑了期望产出,而忽略了在经济发展过程中产生的非期望产出,因此更多的研究人员采用ML指数法来测算投入效率[2-6].ML指数法是采用DEA法来计算距离函数,生产前沿面是以当期的数据构成的,忽略了产出的短期波动对生产前沿面造成的影响.Oh等[7]在ML指数的基础上提出了sequential Malmquist-Luenberger(SML)指数法,并运用该方法测算了26个经济合作与发展组织(Organization for Economic Co-operation and Development,OECD)成员国的投入效率,该方法在一定程度上解决了短期波动对生产前沿面造成的影响.长江经济带是长江流域最发达的地区,也是全国高密度的经济走廊之一,采用科学的方法研究长江经济带投入效率的时空差异意义重大.本工作在SML指数法的基础上,构建了在环境约束下长江经济带投入效率的SML指数模型;将该模型运用于长江经济带的分析,以技术进步指数和效率变化指数来反映长江经济带的投入效率,并对在环境约束下长江经济带投入效率的时空差异进行研究,以期为提高长江经济带的投入效率提供决策支持.

1 基于SML指数的投入效率测算模型

1.1 序列生产可能性集与方向性距离函数

定义1 设当期生产可能性集:P(xt)={(yt,bt):投入xt能够产出yt和bt},t=1,2,···,T,这里的生产可能性集只考虑在t时期的参考值.其中,xt∈RN为投入变量,yt∈RM为期望产出变量,bt∈RI为非期望产出变量,N为投入变量个数,M为期望产出变量个数,I为非期望产出变量个数.

定义2[7]序列生产可能性集:在t时期的序列生产可能性集是由时刻1到t的所有生产可能性集共同构成,即(xt)=P1(x1)∪P2(x2)∪P3(x3)∪···∪Pt(xt),1≤ t≤ T,T为总的时间长度.

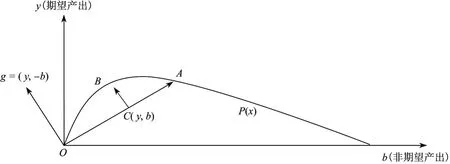
图1 序列生产可能性集Fig.1 Sequential production possibility set

假设生产可能性集P(x)具有如下3个性质,即非期望产出具有弱处置性、期望产出自由处置性及期望与非期望产出间的零联合性.当P(x)满足以上第1和第3条假设时,其大致形状如图1所示.图1中,点C为一个产出观测点,在投入x不变的情况下,点C沿着方向向量g移动,可以获得点B的理想产出集,也就是说如果一个决策单元以最佳方式进行生产,则可以最大限度地增加期望产出同时降低非期望产出,从而将产出观测点由点C移动到了点B.如果点C按照Shepherd距离函数[8]里定义的期望产出和非期望产出同时扩大的方向移动,那么最终产出观测点C移动到了点B.

定义3[4]方向性距离函数表示在投入为x、生产可能性集为P(x)的条件下,期望产出按一定比例增大时,非期望产出按同比例减小的可能性,表示为g=gy−gb,式中gy为期望产出增大的比例,gb为非期望产出减少的比例,考虑到gb为非期望产出,故用负值来表示.这样本工作将方向性距离函数与序列生产可能性集结合到一起,得到了基于产出的方向性距离函数:

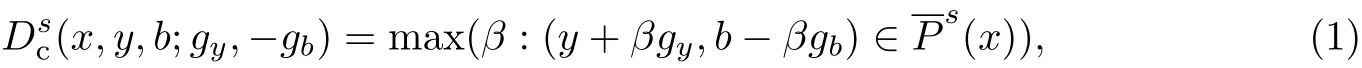
式中,s表示从t到t+1时期x)为序列生产可能性集合.式(1)表示在投入变量为x、生产可能集为x)的条件下,产出向量(y,b)能够沿着方向向量g=gy−gb进行收缩和扩张的最大倍数为β,下标c为本工作考虑在规模报酬不变的情况下投入效率的测算.在规模报酬不变的情况下,根据式(1)可以推出4个方向性距离函数,即在t时期的投入产出变量(xt,yt,bt)在t时期的方向性距离参数为

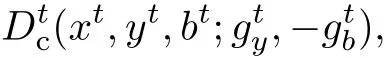
在t+1时期的方向性距离参数为

t+1时期的投入产出变量(xt+1,yt+1,bt+1)在t时期的方向性距离参数为

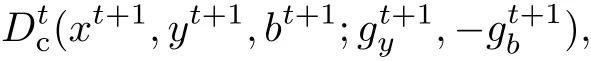
在t+1时期的方向性距离参数为

1.2 基于SML指数法的投入效率测算模型

Chung等[1]在研究Malmquist生产率指数的基础上,结合方向性距离函数与当期生产可能性集,提出了考虑非期望产出的ML指数.Oh等[7]在ML指数的基础上提出了SML指数.本工作在SML指数法的基础上,构建了在环境约束下长江经济带投入效率的SML指数模型;将该模型运用于长江经济带的分析中,以技术进步指数和效率变化指数来反映长江经济带的投入效率,并对在环境约束下长江经济带投入效率的时空差异进行研究.为了区别于ML指数法,本工作用PSTECH与PSEFFCH分别表示技术进步指数和效率变化指数,考虑环境因素的投入效率PSML=PSTECH×PSEFFCH.PSML=1,表示投入效率不变;PSML＜1,表示投入效率呈下降趋势;PSML＞1,表示投入效率呈逐渐上升趋势.

SML指数法的计算公式及其分解情况如式(2)～(4)所示,对于每个决策单元都有与之对应的4个方向性距离函数,式(5)和(6)为第k个决策单元的2个方向性距离函数,其余2个方向性距离函数的求法与式(5)和(6)类似.

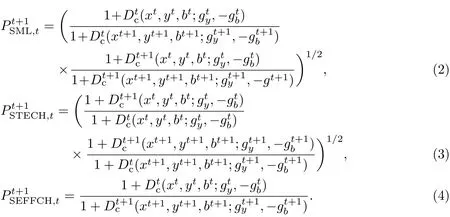
第k个决策单元的方向性距离函数的具体求法如下:

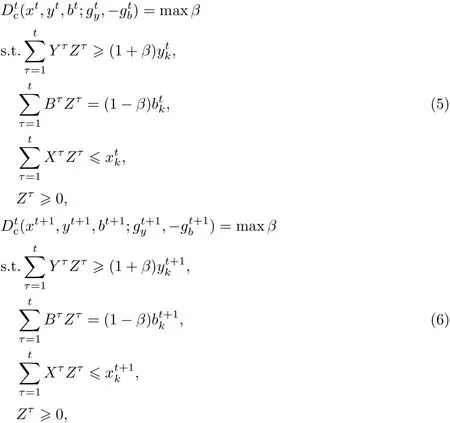
式中,Yτ为M×K矩阵,表示在τ时期的期望产出;K为决策单元的个数;M为期望产出变量的个数;Bτ为I×K矩阵,表示在τ时期的非期望产出;I为非期望产出变量的个数;Xτ为N×K矩阵,表示在τ时期的投入;N为投入变量的个数;y,b,x分别为M×1,I×1,N×1的3个向量;Zτ为K×1的向量.

2 环境约束下长江经济带投入效率测度的实证研究

长江经济带覆盖11个省市,面积约250万平方公里,包含12个一、二级中心城市,15个地区中心城市,人口和生产总值均超过全国的40%.2014年国务院印发《关于依托黄金水道推动长江经济带发展的指导意见》中提出,依托长江黄金水道,构建沿海与中西部相互支撑新格局,打造陆海双向对外开放新走廊.长江经济带的发展已经成为国家战略,对促进中国经济发展、缩小东中西部地区发展有重要意义.而长江经济带各地区的经济发展在时间与空间上均存在差异,探究长江经济带的投入效率,研究长江经济带各城市经济发展方式对推动长江经济带供给侧结构改革具有深远意义.

2.1 决策单元的选取和数据的获取

从空间分布规律来看,长江经济带由5个城市群组成:长江三角洲城市群、长江中游城市群、成渝城市群、黔中和滇中城市群,其中前3个为主要城市群.本工作选取的决策单元为组成长江经济带三大二小城市群的15个城市,其中上海、南京、合肥、杭州、宁波和苏州为长江三角洲城市群的代表城市,武汉、长沙、南昌为长江中游群代表城市,宜宾、泸州、重庆、成都为成渝群代表城市,贵阳和昆明分别属于黔中和滇中城市群.由于重庆市在1997年正式成立,因此计算时所选择的变量数据以2000年为基期.本工作测算2000年至2013年长江经济带城市群15个主要城市在环境约束下的投入效率,数据均来源于《中国城市统计年鉴》《中国统计年鉴》,其中缺失的数据采用时间序列进行拟合得到.

2.2 投入产出变量的选取

对于投入指标,本工作选取劳动投入与资本投入作为投入指标.对于劳动投入,本工作采用长江经济带15个主要城市2000年至2013年末单位从业人数作为劳动要素投入的衡量指标.对于资本投入,本工作采用人均资本存量作为资本投入变量.资本存量的计算采用国际上通用的永续盘存法(perpetual inventory method,PIM)估算资本投入.对于折旧率与基期资本存量,本工作均采用张军等[9]的研究结果.

对于期望产出指标,选取各城市人均实际GDP作为期望产出指标.研究人员在非期望产出指标的选取上具有较大的弹性,Kaneko等[10]和Managi等[11]选择了废气、废水和固体废物作为非期望产出;Watanabe等[12]和涂正革[13]选择SO2作为非期望产出;张建升[4]考虑将“废水排放量”作为非期望产出.长江流域森林植被锐减,水质污染严重,大量污水排入导致长江生态环境遭到严重破坏[14].因此,本工作选取每万元产值的工业废水排放量作为非期望产出指标.

2.3 在环境约束下长江经济带投入效率的空间分布特征

从空间分布来看,沿长江下游至上游,长江经济带分布着长江三角洲城市群、长江中游城市群、成渝城市群、黔中和滇中城市群,在这5大城市群中前3个为主要城市群.由于黔中和滇中城市群均为较小的城市群,因此将其作为一个整体进行考虑.本工作运用R语言软件,采用SML指数模型对长江经济带在城市群环境约束下的投入效率进行分析,具体结果如表1所示.

从分析单个城市视角可以看出如下几个情况.①长江经济带主要的15个城市在考虑环境因素时的投入效率均大于1,说明从2000年到2013年各城市整体经济增长效率呈上升趋势,且绝大多数城市的技术进步指数平均增长率在2%以上,表明各个城市在发展过程中,逐步由原有的粗放型经济增长方式向集约型经济增长方式转变,且积极采用新技术、新工艺,以创新理念增强发展动力.②在15个城市中,上海市与苏州市在环境约束下投入效率的增长率均在8%以上,且两个城市均属于长江三角洲城市群,这也体现了在长江经济带的建设过程中,长江三角洲城市群起着不可替代的龙头作用.③在长江经济带主要的15个城市中,南京、上海、合肥、苏州、宁波、成都、武汉和长沙的投入效率高于长江经济带的平均水平,说明长江经济带经济在由投入型增长转向效率型增长的过程中,这些城市起到了较好的带头作用.

从分析城市群视角也可以看出如下几个情况.①长江三角洲城市群在环境约束下的投入效率明显高于其他城市群,增长率的平均值为6.75%,可见技术进步是快速增速的主要原因.②长江中游城市群在环境约束下的投入效率仅次于长江三角洲城市群,2000年到2013年的平均增长率为6.19%,长沙与武汉的年均增长率均在7%以上;黔中和滇中城市群在环境约束下的投入效率增长率最低,平均值仅为2.90%,低于长江经济带的平均水平.这些反映了长江上游地区的经济增长主要依靠要素投入,同时污染物排放量仍较大;长江中游在“中游崛起”、“两型”社会建设综合配套改革试验区等战略和措施的指引下,创新绿色发展能力逐步增强.③长江三角洲城市群的技术进步指数明显高于其他城市群,说明在发展过程中,虽然长江三角洲城市群注重创新要素的提升,但其效率变化指数却不很理想,且趋近于负增长.效率变化指数是指产业结构能否符合总体要求并使之发挥最大的经济利益和社会效益,长江三角洲城市群的效率变化指数较低,说明近些年由于环境的约束其产业结构的调整和城市转型面临着诸多困难,不能发挥最大的经济效益.

表1 在环境约束下长江经济带投入效率空间分布特征Table 1 Spatial distribution characteristics of investment eきciency about Yangtze River Economic Belt under the restriction of environment

2.4 环境约束下长江经济带投入效率的时间演变特征

为了进一步分析长江经济带投入效率在时间维度上的动态变化情况,本工作对长江经济带15个主要城市从2000年至2013年在环境约束下的投入效率进行计算,得到了这15个主要城市总体投入效率及分解数据(见表2),以及在考虑环境因素时投入效率的变化趋势(见图2).

研究发现,长江经济带从2000年至2013年在环境约束下投入效率的动态变化平均值为1.051 3,这表明其投入效率改善上升了5.13%;整体投入效率水平均大于1,说明长江经济带整体经济增长效率呈递增趋势,表明中国近几年出台的环境政策对于改善环境问题和转变生产方式产生了一定积极的影响.同时从图2中可以看出,技术进步指数的变化趋势与在环境约束下投入效率的变化趋势基本一致,进一步表明长江经济带投入效率的提高,即经济增长效率水平的提升主要是由于技术进步,而不是效率变化.其次,2000年至2007年长江经济带在环境约束下的投入效率整体呈上升趋势,增长率的最大值达到7.43%;从2008年开始呈下降趋势,2009年增长率下降为4.12%.这主要是由于2008年源于美国世界范围的经济危机,导致全球经济和金融震荡.中国处于这样的大环境中,虽然实行保增长、反膨胀的宏观调控,但是为了保增长,中国经济增长的质量还是有所下降.最后,2009年以后投入效率又出现回升趋势,这可能是因为中国积极的调控政策致使国家经济开始逐步复苏.

表2 环境约束下长江经济带投入效率时间演变特征Table 2 Temporal distribution characteristics of investment eきciency about Yangtze River Economic Belt under the restriction of environment

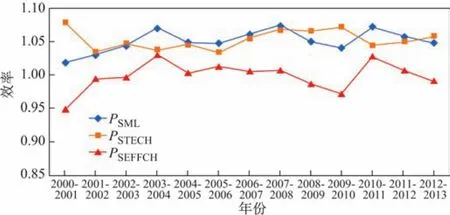
图2 在考虑环境因素时长江经济带的投入效率变化趋势Fig.2 Variation tendency of investment eきciency about the Yangtze River Economic Belt under the restriction of environment

3 结论

本工作通过构建在环境约束下长江经济带投入效率的SML指数模型,运用R语言软件测算了长江经济带主要15个城市在考虑环境因素下的投入效率及其分解情况,得到如下结论.

(1)长江经济带作为中国综合实力最强、战略支撑作用最大的区域之一,在环境约束下的投入效率随时间的演变呈上升—下降—上升的变化趋势.在2000年至2013年之间,长江经济带整体的投入效率呈现上升趋势,长江经济带2013年投入效率较2000年上升了5.13%;技术进步指数的变化趋势与投入效率的变化趋势基本一致,进一步表明长江经济带投入效率的提高主要是由于技术的进步,而不是效率的变化.

(2)从空间上看,长江经济带15个城市在考虑环境因素时的投入效率均大于1,且技术进步是推动各个城市投入效率提高的主要原因,表明各个城市在发展过程中,逐步由原有的粗放型经济增长方式向集约型经济增长方式转变,且通过积极采用新技术、新工艺,以创新理念增强发展动力.从各个城市群投入效率的变化情况来看,沿着长江自上游至下游,各城市群的投入效率呈逐步上升的变化趋势.其中长江三角洲城市群投入效率明显高于其他城市群,黔中和滇中城市群则为最低.这表明,相较于长江中下游城市群,长江上游城市群的经济发展主要依靠要素投入,同时总的污染物排放仍在高水平上,环境污染仍然非常严重.长江三角洲城市群的技术进步指数明显高于其他城市群,但其效率变化指数却不如成渝城市群和长江中游城市群.这进一步说明效率变化指数的恶化是阻碍各城市投入效率提高的主要原因.

针对本工作的研究发现,提出以下几点建议.①在发展过程中,长江经济带首先应解决生态治理问题,建立完善的长江流域生态补偿机制以及污染联防联控应急预警机制,推进要素投入组合结构调整.②长江经济带是“一带一路”的关键,中国在长江经济带建设过程中,应努力提高技术效率对投入效率的贡献,同时践行创新驱动发展战略,促进经济转型升级发展和经济增长质量的提升.③加强各城市群之间的协作,充分发挥长江经济带的龙头作用,促进“东中西”3大区域经济和“上中下”3大城市群的协调发展,促进中上游地区有序承接产业转移,带动黔中和滇中城市群的发展.另外,上海市作为长江经济带上的龙头城市,更应对沿江开放起到引领带动作用,实现要素和资源的交换与集散,促进区域协调发展.

[1]CHUNG Y,F¨ARE R,GROSSKOPF S.Productivity and undesirable outputs:a directional distance function approach[J].Journal of Environmental Management,1997,51(3):229-240.

[2]田银华,贺胜兵,胡石其.环境约束下地区全要素生产率增长的再估算:1998—2008[J].中国工业经济,2011(1):47-57.

[3]李静,陈武.中国工业的环境绩效与治理投资的规模报酬研究[J].华东经济管理,2013(3):44-50.

[4]张建升.环境约束下长江流域主要城市全要素生产率研究[J].华东经济管理,2014(12):59-63.

[5]F¨ARE R,GROSSKOPF S,PASURKA C A.Environmental production functions and environmental directional distance functions[J].Energy,2007,32(7):1055-1066.

[6]KUMAR S.Environmentally sensitive productivity growth:a global analysis using Malmquist—Luenberger index[J].Ecological Economics,2006,56(2):280-293.

[7]OH D,HESHMATI A.A sequential Malmquist-Luenberger productivity index:environmentally sensitive productivity growth considering the progressive nature of technology[J].Energy Economics,2010,32(6):1345-1355.

[8]SHEPHERD R W.Multilateral productivity comparisons with undesirable outputs[J].Economic Journal,1970,93:883-891.

[9]张军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952—2000[J].经济研究,2004(10):35-44.

[10]KANEKO S,MANAGI S.Environmental productivity in China[J].Economics Bulletin,2004,17(2):1-10.

[11]MANAGI S,KANEKO S.Economic growth and the environment in China:an empirical analysis of productivity[J].International Journal of Global Environmental Issues,2006,6(1):89-133.

[12]WATANABE M,TANAKA K.Eきciency analysis of Chinese industry:a directional distance function approach[J].Energy Policy,2007,35(12):6323-6331.

[13]涂正革.环境,资源与工业增长的协调性[J].经济研究,2008(3):93-105.

[14]李红清.长江流域自然保护区建设现状与生态保护[J].长江流域资源与环境,2011,20(2):150-155.