一类时间尺度上三阶非线性时滞动态方程的振动性

隋 莹,韩振来

(济南大学 数学科学学院,山东 济南 250022)

1990年，Hilger[1]发表了时间尺度上微积分理论，吸引了全世界数学家们的广泛关注，发表了许多关于时间尺度上动态方程研究成果、专著等，论文可参阅文献[4-22].本文将考虑下面一类时间尺度上带有阻尼项的三阶非线性动态方程的振动性问题：

(r2(r1(yΔ)α)Δ)Δ(t)+p(t)(yΔ)α(σ(t))+q(t)f(y(g(t)))=0，t≥t0>0.

(1)

这里α≥1是正奇数的比，设

1)r1,r2,p,q∈Crd(I,R+),r2Δ(t)≥0,其中I=[t0,∞)T，R+=(0,∞)T.

3)f∈C(R,R),xf(x)>0，f(x)/xβ≥k>0,x≠0，其中β为常数，是正奇数的比.

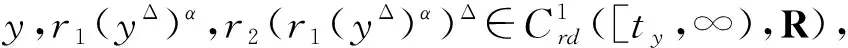
运用Riccati变换和不等式技巧，在相关的二阶动态方程

(2)

振动的条件下，给出使方程(1)所有解振动的充分条件.

1 预备知识

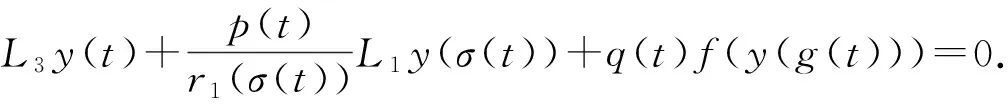
假设

R1(t,t0)→∞,t→∞,

(3)

R2(t,t0)→∞,t→∞,

(4)

下面给出主要结果证明中所用到的引理.

引理若

(r2xΔ)Δ(t)+p(t)x(h(σ(t)))≤0,

(5)

有最终正解，其中h(t)≤t.则方程

(r2xΔ)Δ(t)+p(t)x(h(σ(t)))=0

(6)

有最终正解.

证明设x是不等式(5)的最终正解,x(t)>0,x(h(σ(t)))>0,t≥t0,则有(r2xΔ(t))Δ≤0.

因此，存在t1≥t0,当t≥t1时，有xΔ(t)>0,或者当t≥t1时，有xΔ(t)<0.若是后者，则有

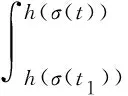
则式(5)可以写成

(7)

对方程(7)从t到u≥t≥t1积分,并令u→∞得

现定义数列{zj(t)}j∈N0:z0=y(t)，

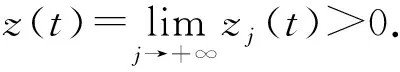
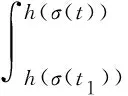
(8)

(r2vΔ)Δ(t)=(r2z)Δ(t)=-p(t)v(h(σ(t))),

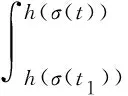
2 振动准则

通过Riccati变换的方法，建立方程(1)的振动准则.

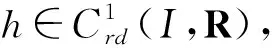
(9)

或

(10)

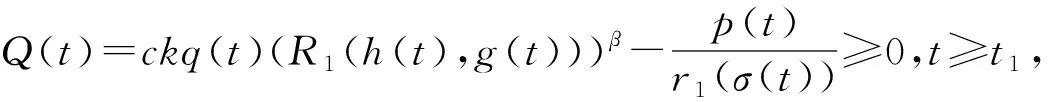
证明设y是方程(1)在[t1,∞)T,t1≥t0上的一个非振动解,不失一般性,可以假设y(t)>0,y(g(t))>0,t≥t1.若在[t1,∞)T上L1y>0,则由方程(1)可得

其中x=L1y>0.则由引理得，方程(2)有正解，推出矛盾.接下来,假设在[t1,∞)T上L1y<0.考虑函数L2y,当t充分大时,L2y(t)≤0不成立,其中t≥t2≥t1.通过对下列不等式两边积分

(11)

则由式(3) 式得,对充分大的t有y(t)<0,得到矛盾.因此,设对于充分大的t有y(t)>0,L1y(t)<0,

L2y(t)≥0,t≥t3≥t2.对于v≥u≥t3,有

令u=g(t),v=h(t),得到y(g(t))≥R1(h(t),g(t))(-L1y(h(t)))1/α=R1(h(t),g(t))x(h(t)),其中x(t)=(-L1y(t))1/α>0,t≥t3.由方程(1)知，x是递减的.因为g(t)≤h(t)≤t,得到

这里z(t)=xα(t).由于z(t)是递减的,α≥β,则存在一个常数c4>0，使得zβ/α-1(t)≥c4.因此

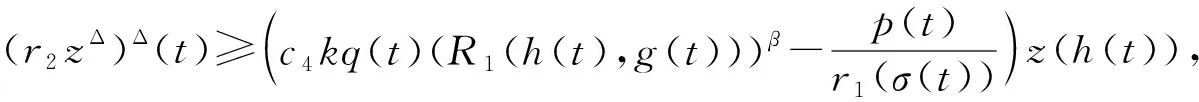
(r2zΔ)Δ(t)=Q(t)z(h(t)).

(12)

对于v≥u≥t1，有

(13)

在式(13)中,令u=h(s),v=h(t),t≥s≥t1，得

z(h(s))>-R2(h(t),h(s))r2(h(t))zΔ(h(t)).

h(t)≥t1，且t对式(12)积分,得

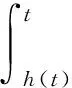
即

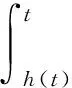
(14)

当t→∞时在式(14)的两端取上极限，与式(9)矛盾.

接下来,从u到t对式(12)积分，得

(15)

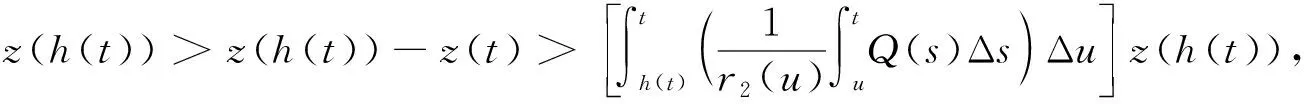
(16)

当t→∞时在式(16)的两端取上极限，与式(10)矛盾，证毕.

最后,可以很容易把定理1推广到方程

(r2(r1(yΔ)α)Δ)Δ(t)+p(t)(yΔ(h(σ(t))))α+q(t)f(y(g(t)))=0,

(17)

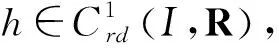
定理2设式(3)和式(4)成立,α≥β,假设方程

(18)

证明设y是方程(17)在[t1,∞)T,t1≥t0上的一个非振动解，不失一般性，可以假设y(t)>0,y(g(t))>0,t≥t1.如果在[t1,∞)T上L1y>0,那么由方程(17)可得

其中x=L1y>0.由引理得，方程(18)有正解，推出矛盾.当在[t1,∞)T上L1y<0时，证明类似于定理1,因此忽略.

3 验证

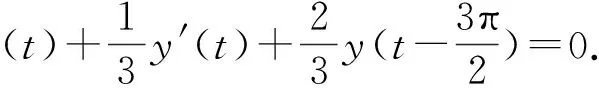
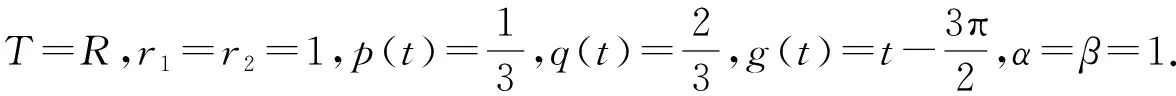
m(t)=1.可以得到

参考文献：

[1] HILGER S.Analysis on measure chains-a unified approach to continuous and discrete calculus [J].Results Math,1990，18：18-56.

[2] BOHNER M,PETERSON A.Dynamic equations on time scales,an introduction with applications[M].Boston:Birkhäuser,2001.

[3] 韩振来,孙书荣.时间尺度上动态方程的振动理论[M].济南:山东大学出版社,2014.

[4] AGARWAL R P,BOHNER M,SAKER S H.Oscillation of second order delay dynamic equations[J].Canadian Applied Mathematics Quarterly,2005，13(1)：1-18.

[5] HAN Z L,SUN S R,SHI B .Oscillation criteria for a class of second order Emden-Fowler delay dynamic equations on time scales[J].Journal of Mathematical Analysis and Applications，2007，334(2)：847-858.

[6] ERBE L,HASSAN T,PATER A.Oscillation criteria for nonlinear damped dynamic equations on time scales[J].Applied Mathematics and Computation,2008,203(1):343-357.

[7] 孙书荣，韩振来，张承慧.时间尺度上二阶Emden-Fowler中立型时滞动力方程的振动准则[J].上海交通大学学报,2008，42(12)：2070-2075.

[8] 韩振来，孙书荣，张承慧.时间尺度上二阶中立型时滞动力方程的振动性[J].中山大学学报(自然科学版),2010,49(5):21-24.

[9] SUN S R,HAN Z L,ZHANG C H .Oscillation of second-order delay dynamic equations on time scales[J].Journal of Applied Mathematics and Computing,2009,30(1/2):459-468.

[10] LI T X,HAN Z L,SUN S R,et al.Oscillation results for third order nonlinear delay dynamic equations on time scales[J].Bulletin of the Malaysian Mathematical Society,2011,34(3):639-648.

[11] 孙一冰,徐美荣,李同兴,等.时间尺度上二阶具阻尼项Emden-Fowler型动力方程振动性[J].滨州学院学报,2011,27(6):13-17.

[12] HAN Z L,LI T X,SUN S R,et al.Oscillation criteria for third order nonlinear delay dynamic equations on time scales[J].Annales Polonici Mathematici，2010，99(2)：143-156.

[13] 潘元元,韩振来.时标上二阶中立型时滞动力方程的振动性[J].济南大学学报,2012,26(2):191-194.

[14] 李同兴,韩振来,张承慧,等.时间尺度上三阶Emden-Fowler时滞动力方程振动准则[J].数学物理学报,2012,32A(1):222-232.

[15] HAN Z L,LI T X,SUN S R,et al.Oscillation of second order quasilinear neutral delay differential equations[J].Journal of Applied Mathematics and Computing,2012,40(1/2):143-152.

[16] 孙一冰,韩振来,孙书荣,等.时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性[J].应用数学学报,2013,36(3):480-494.

[17] 张全信,高丽,刘守华.时间尺度上具阻尼项的二阶半线性时滞动力方程振动性的新结果[J].中国科学:数学，2013，43(8):793-806.

[18] LI H,HAN Z L,WANG Y Z.Nonoscillatory solutions for super-linear Emden-Fowler type dynamic equations on time scales[J].Electronic Journal of Qualitative Theory of Differential Equations,2015,2015(53):1-13.

[19] WANG Y Z,HAN Z L,SU S R,et al.Hille and nehari type oscillation criteria for third-order Emden-Fowler neutral delay dynamic equations[J].Bulletin of the Malaysian Mathematical Society,2017,40(3):1187-1217.

[20] SHI Y L,HAN Z L,HOU C X.Oscillation criteria for third order neutral Emden-Fowler delay dynamic equations on time scales[J].Journal of Applied Mathematics and Computing,2017,55:175-190.

[21] HASSAN T S.Oscillation criteria for higher order quasilinear dynamic equations with Laplacians and a deviating argument[J].Journal of the Egyptian Mathematical Society，2017,25(2):178-185.

[22] DENG X H,WANG Q，ZHOU Z.Oscillation criteria for second order neutral dynamic equations of Emden-Fowler type with positive and negative coefficients on time scales[J].Science China，Mathematics，2017，60(1)：113-132.