Lévy过程驱动的HJM框架下贴现债券价格的解
2018-06-29杜凤娇
杜凤娇
(1.中国矿业大学 数学学院,江苏 徐州 221106;2.徐州工程学院,江苏 徐州 221008)
在布朗运动下,由HJM模型可以得到贴现债券价格的解.本文将布朗运动换成了Lévy过程(关于Lévy过程的详细介绍参见文献[1-2]),它在有限时段内可以有可列无限次跳跃,将模型进一步推广.利用Lévy过程下即期鞅测度方法得到了贴现债券价格过程满足的随机方程,并求出了贴现债券价格的解.使得在布朗运动下由HJM模型得到的贴现债券价格的解成为本文结论的特殊情况.
1 Lévy过程下HJM模型的即期鞅测度
选取现金债券作为计价单位,现金债券Bt满足

到期日为T的债券价格B(t,T)满足动态方程
dB(t,T)=B(t-,T)[a(t,T)dt+b(t,T)dYt].
Yt=cWt+Mt+αt为定义在带流概率空间(Ω,F,(Ft),P)上的一维Lévy过程的标准分解,其中W={Wt,0≤t≤T*}是一维标准布朗运动,M={Mt,0≤t≤T*}为纯跳跃Lévy过程,c和α是常数.假设对所有的h∈(-h1,h2),0 整理得 dB(t,T)=B(t-,T)[(a(t,T)+αb(t,T))dt+cb(t,T)dWt+b(t,T)dMt]. 定义贴现债券价格过程 则有 dZ*(t,T) =d[B(t,T)B-1(t)] 令 则 则 令 则 (1) 定义过程Zt: 其中ε(·)为Doleas-Dale指数半鞅[1]. 则Zt是一个非负鞅,满足Z0=1. (2) 或等价地写为: 定理1令Ρ*为FT上关于测度Ρ绝对连续的测度,定义即期鞅测度Ρ*满足: 在测度Ρ*下,贴现债券价格过程是一个鞅,并且满足方程: dZ*(t,T)=-Z*(t,T)[σ*(t,T)cdWt*+σ*(t,T)dMt*], (3) 即 dZ*(t,T)=Z*(t-,T)[-σ*(t,T)cdWt*-σ*(t,T)dMt*]. 由Dole′as-Dale公式 从而 (4) 该结果为布朗运动下由HJM模型所得结果,可以看作本章的特殊情况. 本文构造了Lévy过程下HJM模型的即期鞅测度Ρ*,得到了在即期鞅测度Ρ*下贴现债券价格满足的随机方程 dZ*(t,T)=-Z*(t,T)[σ*(t,T)cdWt*+σ*(t,T)dMt*]. 得到即期鞅测度下贴现债券价格的解 使得布朗运动下由HJM模型所得结果 成为本文的特殊情况. 参考文献: [1] HE S W,WANG J G,YAN J A.Semimartingale theory and stochastic calculus[M].Beijing:Science Press,1992. [2] SATO K I.Lévy processes and infinitely divisible distributions[M].Cambridge:Cambridge University Press,1999. [3] EBERLEIN E,SEBASTIAN R.Term structure models driven by general Lévy processes[J].Mathematical Finance,1999,9(1):31-53. [4] EBERLEIN E,JACOD J,RAIBLE S.Lévy term structure models:No-arbitrage and completeness[J].Finance and Stochastics,2005(9):67-88. [5] MUSIELA M,RUTKOWSKI M.Continuous-time term structure models:Forward measure approach[J].Finance and Stochastics.2005(1):261-291. [6] MUSIELA M,RUTKOWSKI M.Martingale methods in financial modelling,2nd ed[M].Berlin:Spring-Verlag,2005. [7] CHAN T.Pricing contingent claims on stocks driven by Lévy processes [J].Annal of Applied Probability,1999,9(2):504-528. [8] HARRISON J M,KREPS D M.Martingales and arbitrage in multiperiod securities markets.[J].Ecnomic Theory,1979,20:381-408. [9] HARRISON J M,PLISKA S R.Martingales and stochastic integrals in the theory of continuous trading[J].Stochastic Process,1981,11:215-260.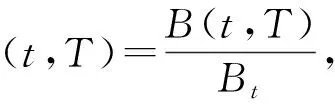
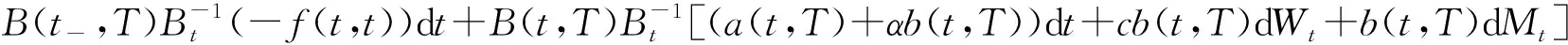


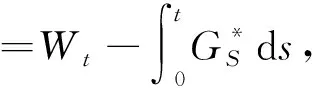
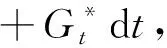
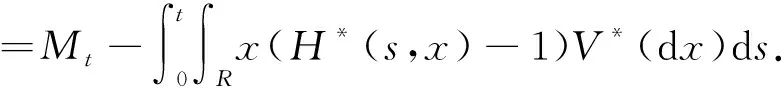

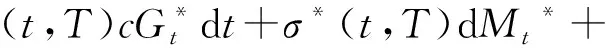

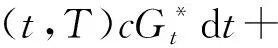
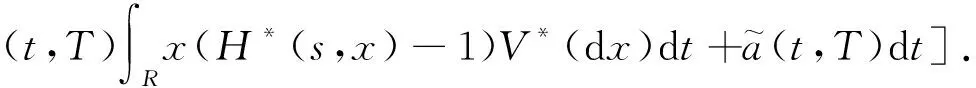
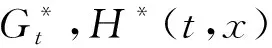
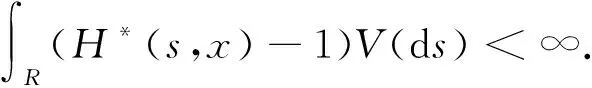


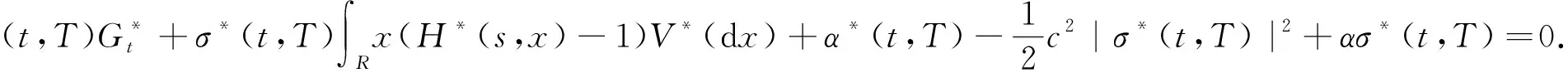

2 即期鞅测度下贴现债券价格的解

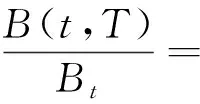
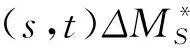
3 结论
