基于区间数TOPSIS法的路面最优预养护方案决策
2018-06-29凌天清陈巧巧崔立龙
凌天清,陈巧巧,崔立龙
(重庆交通大学 土木工程学院,重庆 400074)
路面预防性养护的目的是在路面结构强度尚良好的情况下,充分把握“合适时间、合适措施、合适位置”原则,通过一系列的预防性养护措施,保持路面使用性能良好.从长远来看,预防性养护能有效降低公路经常性养护成本,缓解“资金供给能力不足以满足养护高峰期实际需要”的局势;其核心是用最佳成本效益的预养护方案,追求养护管理的主动性、前瞻性和科学性.但其益处最大程度发挥,只有当实行一整套预防性养护计划时才能得以实现;而目前提及预防性养护,多是将预养护最佳时机和对策独立确定.因此,亟需寻求一种全面适用的决策方法,以突破通常先选定预养护技术再确定其应用时间或先确定预养护时机再比选预养护技术的常规思路,更好地符合预防性养护的特点,更大程度上实现和发挥预防性养护的价值.王朝辉等[1]考虑了不同时间和不同对策组合的多种预防性养护方案,通过建立基于数据包络分析(DEA)的预防性养护时机和对策一体优化模型,从中确定最优方案,但其在确定方案效果评分时,按常规思路,选取专家打分区间中值作为评分值,不恰当也不尽合理.经参与重庆智千科技2017年11月底至12月初就渝北区7段城市道路的预养护方案制定工作发现,尽管拟定多种预养护方案,但经重构优化DEA模型计算,确定的最优预养护方案存在成本最低即最优的倾向,最优方案的选取受到了局限.因此,本文在确定最优方案时,定性指标取值确定为区间数,在很大程度上降低了人为因素的主观影响.
路面预防性养护决策具有多目标、多属性的性质,且其属性评价指标具有不确定性.TOPSIS(technique for order preference by similarity to an ideal solution)法是系统工程中有限方案多目标决策分析的一种常用决策方法,而区间数能很好地保证定性指标信息的完备性,因此研究了基于区间数的TOPSIS法,并将其应用于路面预防性养护方案决策.尤天彗等[2]明确指出,区间数多指标决策问题的难点在于区间数的排序,指标取值在某一区间浮动,而可能存在交叉,使得方案优劣评价产生困难.区间数TOPSIS法在经济管理和工程等领域已有诸多研究.陈瑜等[3]提出了一种改进的区间数TOPSIS工程项目投资评价方法,利用区间数描述不确定的信息,综合考虑指标间的关系,并通过引进辅助点扩大了TOPSIS法的应用范围.王朝晖等[4]研究了基于区间数逼近法的路面使用性能综合评价.王渭明等[5]仅考虑一种理想方案时排序结果不一致的现象,借助TOPSIS法原理,同时考虑正、负理想方案,使得决策结果更为客观、合理.屈文阁[6]利用区间数运算法则获得加权规范化矩阵,基于投影对TOPSIS法进行改进,依据各方案与理想解的相对贴近度进行方案排序或择优.袁琳[7]研究了基于权重为区间数的逼近理想点的多属性决策方法,对知识产权质押融资比选项目的风险进行评价.基于对以上理论与实践的充分理解和把握,本文将区间数TOPSIS法引入至路面预防性养护方案决策中,将定性指标取值量化为区间数,基于离差最大化思想确定各指标权重,采用TOPSIS法对各方案与理想解的相对贴近度进行排序,从而确定最优预养护方案.
1 区间数TOPSIS法
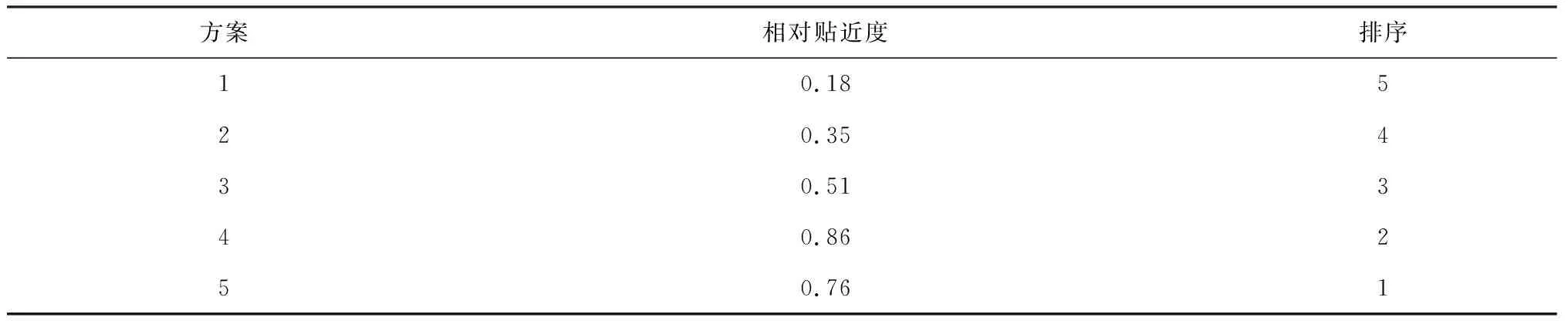
区间数定义是:设a=[aL,aU]={x|0 对涉及多个属性,存在多个目标,且属性、目标间可能产生矛盾的方案排序问题,设由m个方案X1,X2,…,Xm组成比选方案集X={X1,X2,…,Xm},方案的n个属性P1,P2,…,Pn组成属性集P={P1,P2,…,Pn},决策者给出方案Xi在属性Pj下的属性值aij,于是有决策矩阵 (1) 在多属性决策中,属性的类型一般有效益型、成本型、固定型、偏离型、区间型和偏离区间型[8].就路面预防性养护决策实际问题而言,其评价指标类型分为效益型和成本型. 若aij为实数,则按如下方式变换: (2) (3) 若aij为区间数,则 (4) (5) (6) 求解得到 (7) 构造加权规范化矩阵W=(wij),其中wij=bijωj,i=1,2,…,m,j=1,2,…,n. 基于加权规范化决策矩阵W,确定属性值的正、负理想点: I+=(I1+,I2+,…,In+), (8) I-=(I1-,I2-,…,In-), (9) 如bij为实数,则 (10) (11) 如bij为区间数,则 (12) (13) 方案Xi至正、负理想点的距离分别为 (14) (15) 方案Xi与理想点的贴近度 (16) 距“理想方案”最近,同时又离“负理想方案”最远的方案,即为最优方案.因此,按各方案与理想点的贴近度ci值的大小,对方案进行排序,即贴近度ci值越大,该方案越优. 图1 预防性养护决策流程图 以往的路面预防性养护方案制定相关工作多是依据已有检测数据建立性能预测或性能衰变模型,以性能降至触发点或某一规定值时作为预养护最佳时机,进而确定几种措施,比选择优.而以上思路存在以下不足:1)路面技术状况定期检测数据不足,无法用以得到可靠的性能衰变规律;2)仅限于几种预养护措施的比选,而不是长期方案的比较.对于前一方面,由于在役路面检测数据资料的不充分,或是使用年限不长造成的数据不够,因而无法依据已有数据得到可靠的性能衰变规律,此种情况则仅依据本次检测评定结果综合考虑政策、项目预算等,进行路段划分,确定分析期;若能可靠预测路面技术状况性能衰变情况,则依据实际情况判断分析期起点为触发值上限对应时间至性能降至触发值下限,终点为矫正性养护触发上限对应时间或是某一给定年限.本文基于已确定分析期的前提,侧重于最优方案的比选确定.预防性养护决策流程如图1所示. 确定分析期后,自分析期始,以年为间隔制定预养护方案.设本次检测为起始年(第1年),分析期末(性能至触发值或给定年限末年)为第τ年,则拟定如下预养护方案:自第i年(1≤i≤τ,i为整数)开始制定预养护方案,第1种预养护措施至使用寿命,确定下一年仍采用该种或不同预养护措施,依次类推,直至分析期末(第τ年);确定成本时,应考虑措施m的残值.如图2所示. 图2 预养护方案 因此,第i年为起始年时,存在ν种方案.确定的每种方案(方案iv)效果评价指标取值区间见表1. 表1 拟选方案效果评价指标取值 若该措施使用年限小于等于寿命期限,则其效果评分取最高值;若该措施使用年限小于寿命期限中值,则其效果评分取值区间为使用年限线性插值确定的效果评分至最高值;若该措施使用年限大于寿命期限中值,则其效果评分取值区间为最低值至使用年限线性插值确定的效果评分;若该措施使用年限等于寿命期限(制定预养护方案时不会使其使用年限大于寿命期限),则其效果评分取最低值. 若yi≤yiL,则措施i效果评分取值为([ai1U,ai1U],[ai2U,ai2U],…,[aimU,aimU]),或直接表示为(ai1U,ai2U,…,aimU). 若yi=yiU,则措施i效果评分取值为([ai1L,ai1L],[ai2L,ai2L],…,[ainL,ainL]),或直接表示为(ai1L,ai2L,…,aimL). 最优预养护方案可基于区间数TOPSIS法,依据相对贴近度大小排序确定. 以文献[1]中的进行分析,实例选取沧州市某二级公路[1]进行预防性养护,经性能预测回归分析,拟从第3年始至第7年,以4年作为分析期,推荐5个拟选方案(表2). 表2 拟选方案 步骤1:构造决策矩阵.以成本、耐久性、行驶平顺性、抗滑性、防水、美观和降噪7个指标对以上方案进行评估,以确定最优预养护方案.依据文献[1]确定决策矩阵(表3). 表3 决策矩阵 步骤2:依据式(2)~(5)得到规范化矩阵,如下: 步骤3:权重计算并得到加权规范化决策矩阵.依据式(7)得到各指标权重如下: ω=(0.200 5,0.260 1,0.159 5,0.101 6,0.110 9,0.044 9,0.122 5) 得到加权规范化矩阵如下: 步骤4:确定正、负理想点. 步骤5:计算各方案与正、负理想点的距离,对相对贴近度值进行排序.结果见表4. 表4 相对贴近度计算结果 从以上分析可知: 1)指标权重计算得到各因素重要程度排序为耐久性>成本>行驶平顺性>防水>抗滑性>降噪>美观,结果是可信的. 2)从贴近度大小排序来看,方案4最优;而文献[1]中最优方案为方案3,在对其优化DEA方法应用过程中发现,当综合有效系数等于1的决策单元为2个或者更多时,引入最优和最差2个虚拟决策单元重构DEA模型时,结果倾向于成本最小方案为最优方案,因此认为其结果的可靠性值得商榷. 3)方案5相对贴近度大于方案3.从表3可以看出方案五虽成本最高,但其另6个指标评分均远高于方案3,而指标权重是依据离差最大化计算得到的,认为是客观并且可靠的;另外方案2同方案3相比,另6个指标相差不大,而成本较高,因此其相对贴近度较小.因此,方案5优于方案3,这一结果比文献[1]中结果更为可信. 1)属性的权重在很大程度上影响多属性决策问题的结果,本文基于离差最大化思想,直接依据区间数决策矩阵得出各指标的相对重要程度,更为客观、科学.另外,对于路面预防性养护决策来说,决策效果评价指标的权重应结合当地基础设施建设长短期政策、业主要求以及公路等级等因素予以确定,而不应完全相同.因此,在实际项目中,可依照本方法计算或者决策者商讨确定属性权重取值. 2)措施效果指标得分以区间数给出,是对传统评价方法中对定性指标简单打分或取中值的改进,增加了专家对指标赋值的可操作性以及方案的广泛适应性,能够充分表达决策者在该方案中的态度,增加了定性指标取值的客观性. 3)实例分析结果表明,采用基于区间数TOPSIS法进行路面预防性养护方案决策,提高了决策的可靠性和客观性,为预防性养护最优方案决策的理论和实践提供新的思路和实用方法. 4)实例验证部分采用文献[1]的案例,包括预防性养护措施效果分值,为进一步促进区间数TOPSIS法用于预防性养护方案决策,应系统地给出具有广泛适用性的常用预防性养护措施效果评分;另外还应考虑将预养护措施与具体病害状况对应起来,其中包括病害严重程度,以保证确定的预养护方案更具针对性. 参考文献: [1] 王朝辉,王丽君,白军华,等.基于时段的沥青路面预防性养护时机与对策一体优化研究[J].中国公路学报,2010,23(5):27-34. [2] 尤天慧,樊治平.区间数多指标决策的一种TOPSIS方法[J].东北大学学报(自然科学版),2002,23(9):840-843. [3] 陈瑜,张金牡,郭刚,等一种改进的区间数TOPSIS项目投资评价方法[J].武汉工程大学学报,2007,29(3):90-93. [4] 王朝辉,王选仓,马士宾.基于区间数逼近法的路面使用性能综合评价[J].公路交通科技,2009,26(1):21-25. [5] 王渭明,王国富,冯玉国.区间数型多属性决策相对灰色关联分析方法及其应用[J].数学的实践与认识,2012,42(23):75-80. [6] 屈文阁.一种区间数多属性决策方法在经济评价中的应用[J].甘肃科学学报,2013,25(4):152-155. [7] 袁琳.基于区间值TOPSIS法的知识产权融资价值评估风险评价[J].财会月刊,2017(32):55-59. [8] 彭安华,肖兴明.区间数多属性决策中属性值规范化方法[J].机械设计与研究,2011,27(6):5-8.1.1 决策矩阵
1.2 决策矩阵规范化
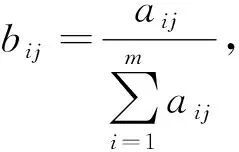
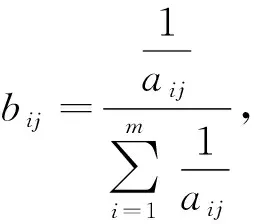
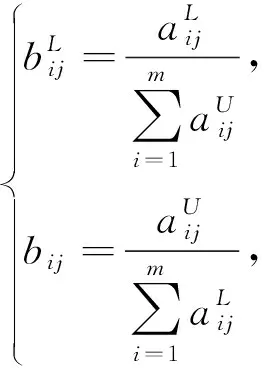

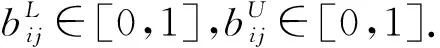
1.3 属性权重向量
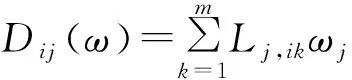
1.4 加权规范化决策矩阵
1.5 正、负理想点
1.6 相对贴近度计算及方案排序
2 预防性养护决策
2.1 预养护决策流程
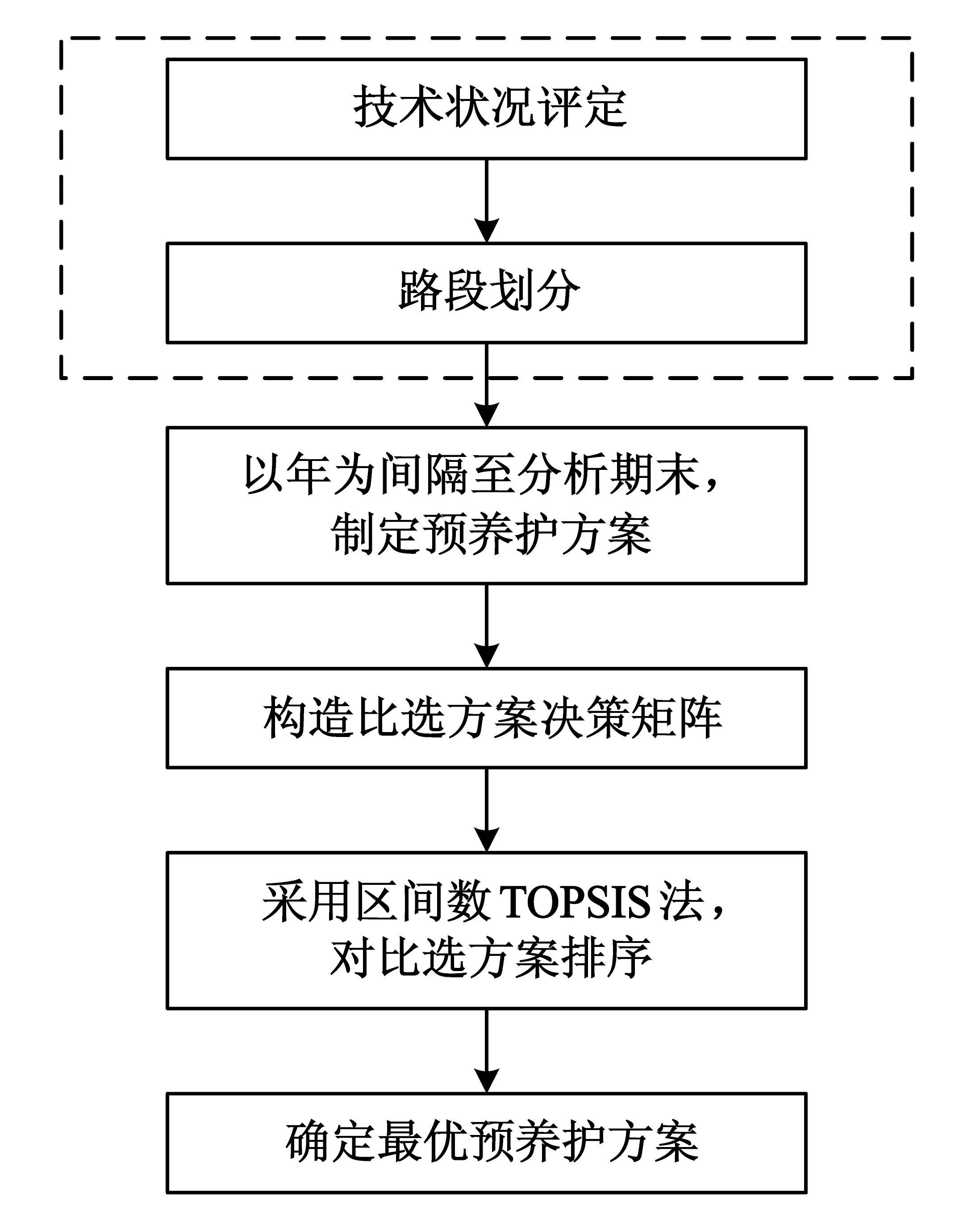
2.2 预养护方案制定


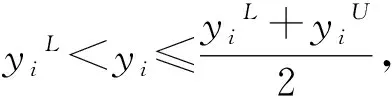
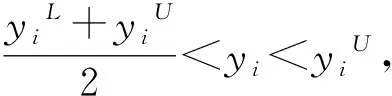
3 实例分析





4 结语
