一类微分方程两点边值问题的神经网络方法应用研究
2018-06-29杨云磊张天乐侯木舟罗建书
杨云磊,张天乐,侯木舟,罗建书
(1.中南大学 数学与统计学院,湖南 长沙 410083;2.国防科技大学 理学院,湖南 长沙 410073)
一直以来,科研人员对微分方程数值解法的研究兴趣经久不衰.物理学、生物学、化学、经济学、人口、资源等领域中的很多问题会通过建立微分方程模型来描述,进而通过数值解进一步分析.关于微分方程两点边值问题数值解法的研究主要有打靶法和差分法等[1].打靶法通过变量代换,将二阶方程降为一阶方程组,利用方程组的数值解法来求解;差分法是微分方程数值解中常用的方法,对两点边值问题同样适用,通过离散并利用差商代替导数,从而将微分方程转化为差分方程求解.关于差分法的研究成果,如离散方法、利用何种差商代替导数、差分方程求解技术等均构成不同的求解两点边值问题的差分方法.
随着人工智能及计算机技术的发展,越来越多的研究人员对神经网络方法产生了浓厚的兴趣.基于神经网络模型的诸多优点,利用神经网络的函数逼近能力,人们研究出了很多采用构造神经网络模型求解微分方程的方法,如:多层感知器神经网络[2-7]、径向基函数神经网络[8-9]、多尺度径向基函数神经网络[10-14]、细胞神经网络[15-16]、有限元神经网络[17]及小波神经网络[7]等.关于微分方程问题的神经网络模型构造的研究主要有采用硬极限函数[18]、Legendre多项式[19]、三角基函数[20]等不同的激活函数、多层感知器[2]、混合技术[21]等构造试验解;关于模型算法的研究主要有基于局部自适应的RPROP算法[22]、DE进化算法[2]、约束积分法[23]、遗传算法[24]等.
本文主要介绍求解一类线性微分方程两点边值问题的神经网络方法,并进行数值实验分析网络拓扑结构及样本量对计算结果的影响.
1 一类线性微分方程两点边值问题的神经网络方法
微分方程两点边值问题的一般形式[1]为:
(1)
在区间a≤x≤b上的数值解法问题.如果函数f是y和y′的线性函数,此时称问题(1)为线性微分方程两点边值问题:
(2)
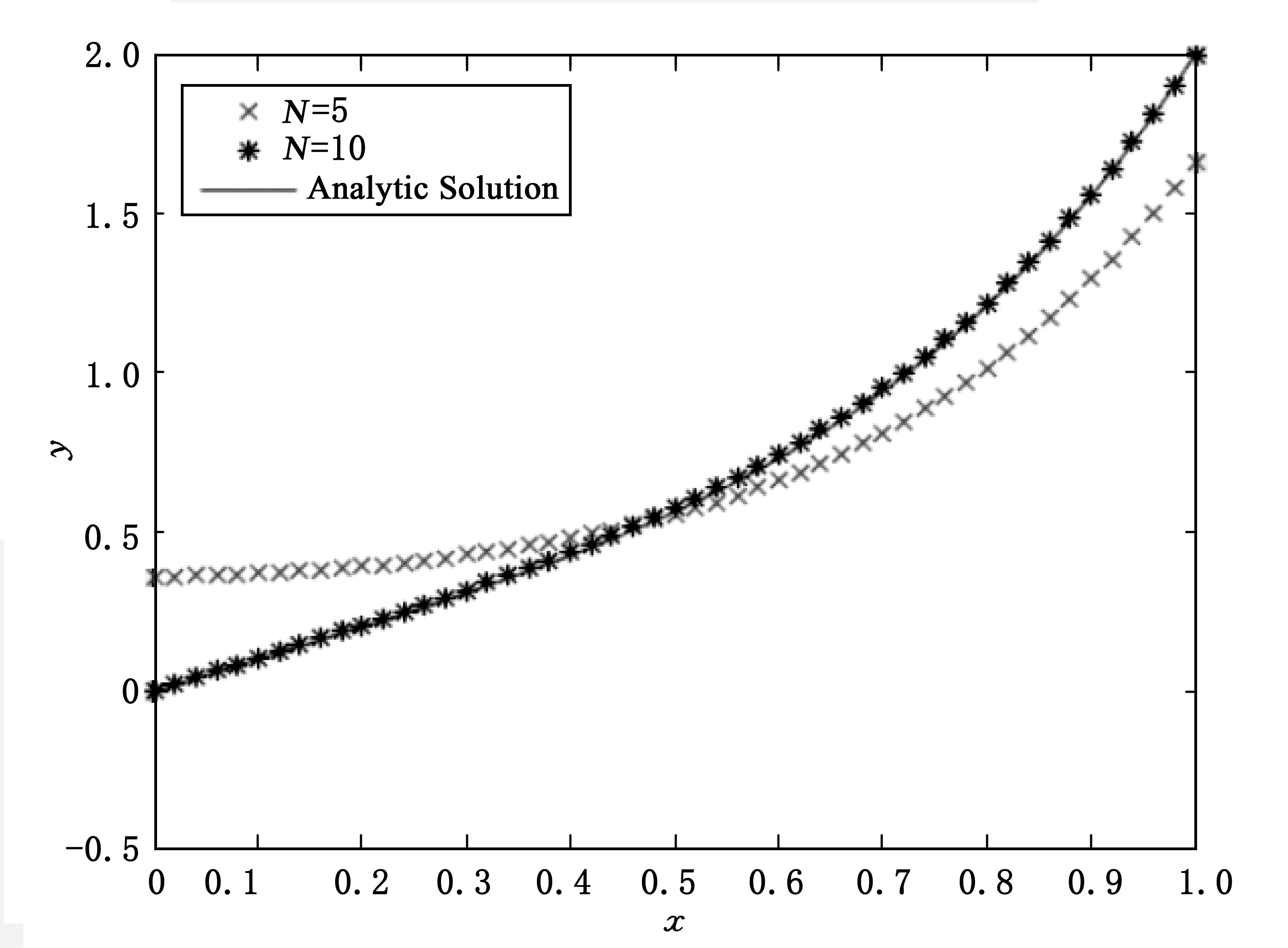
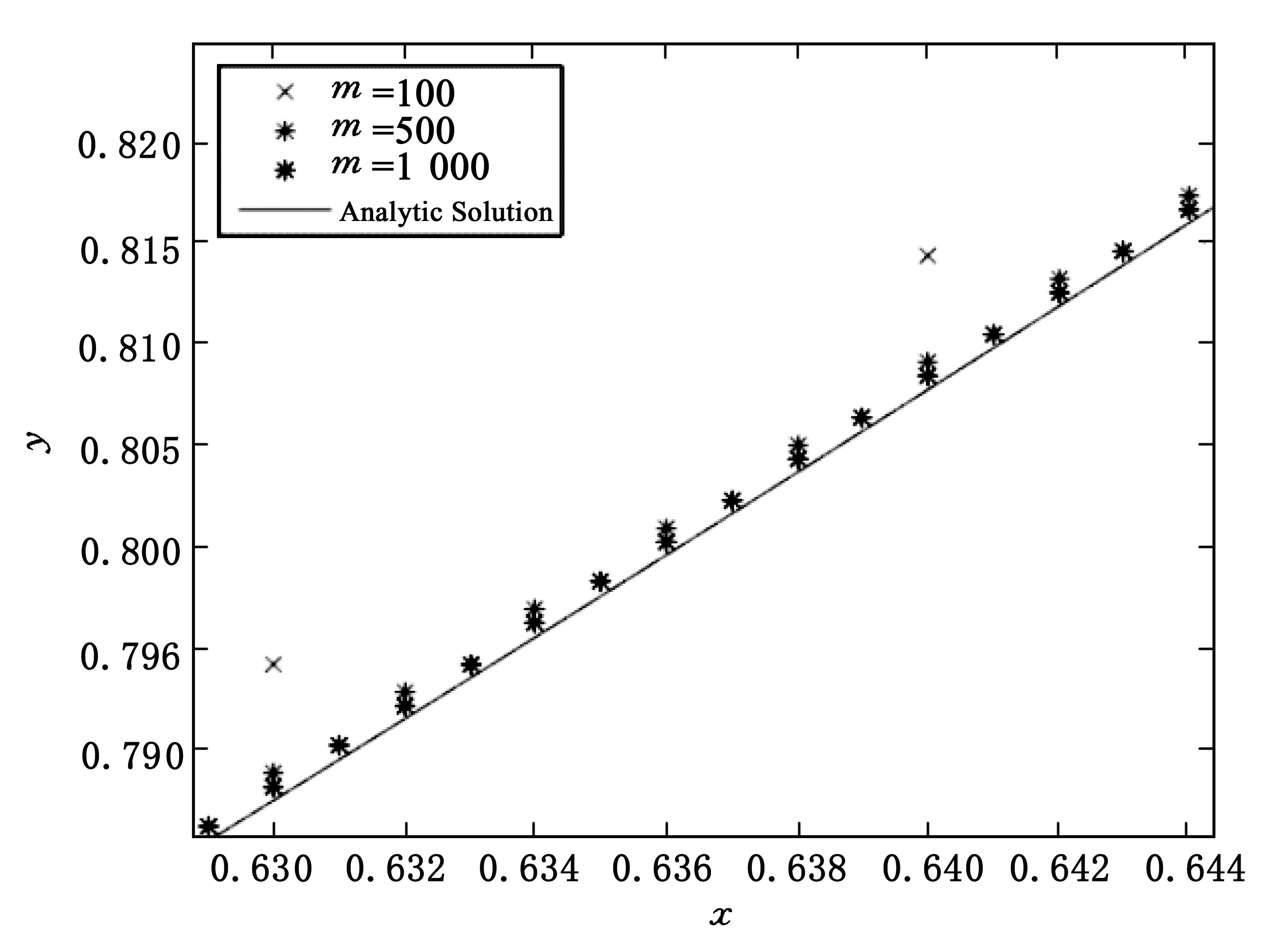
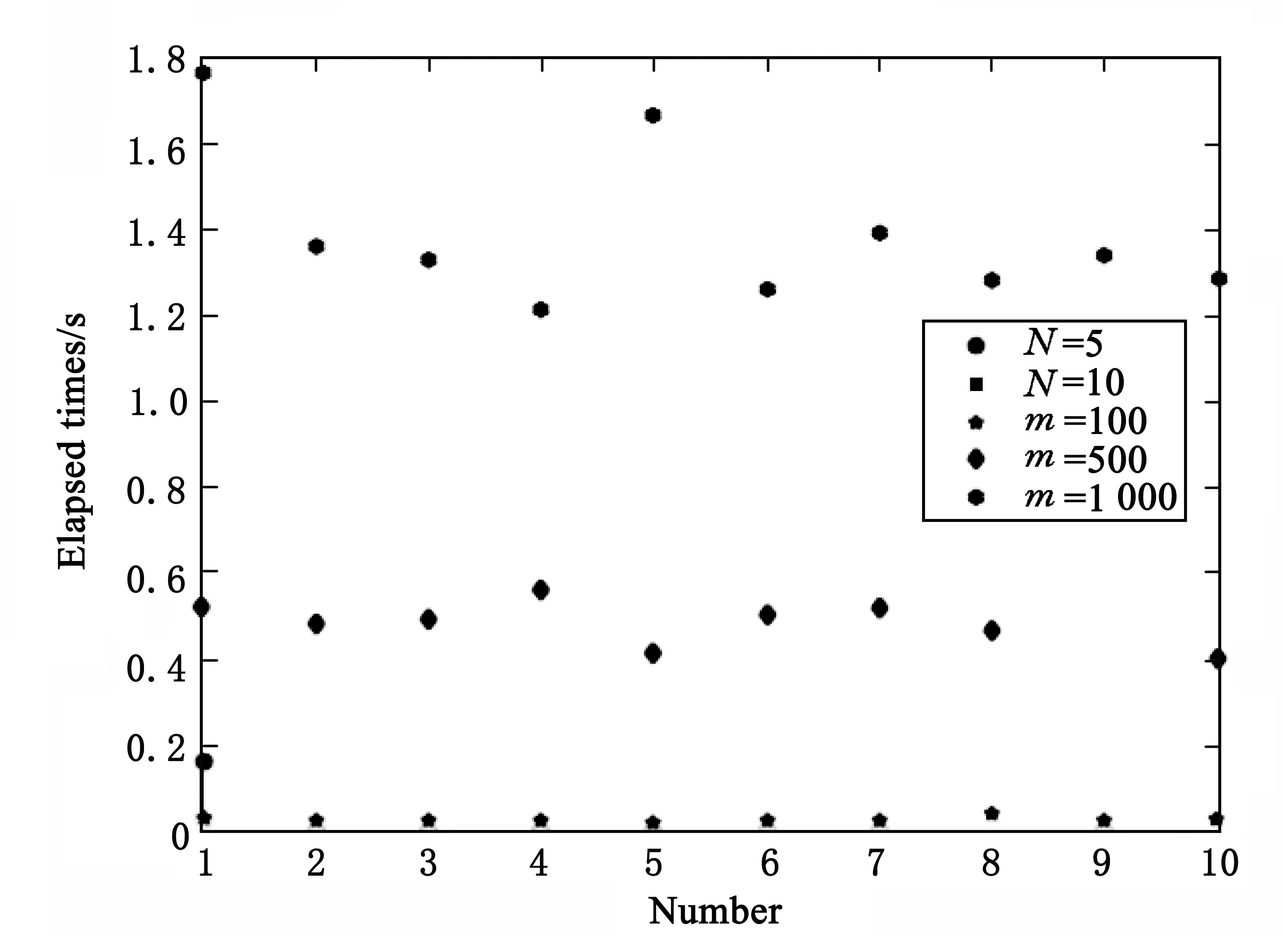
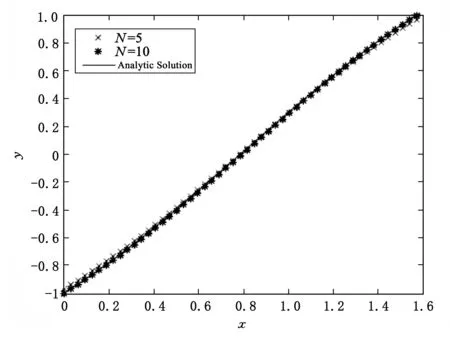
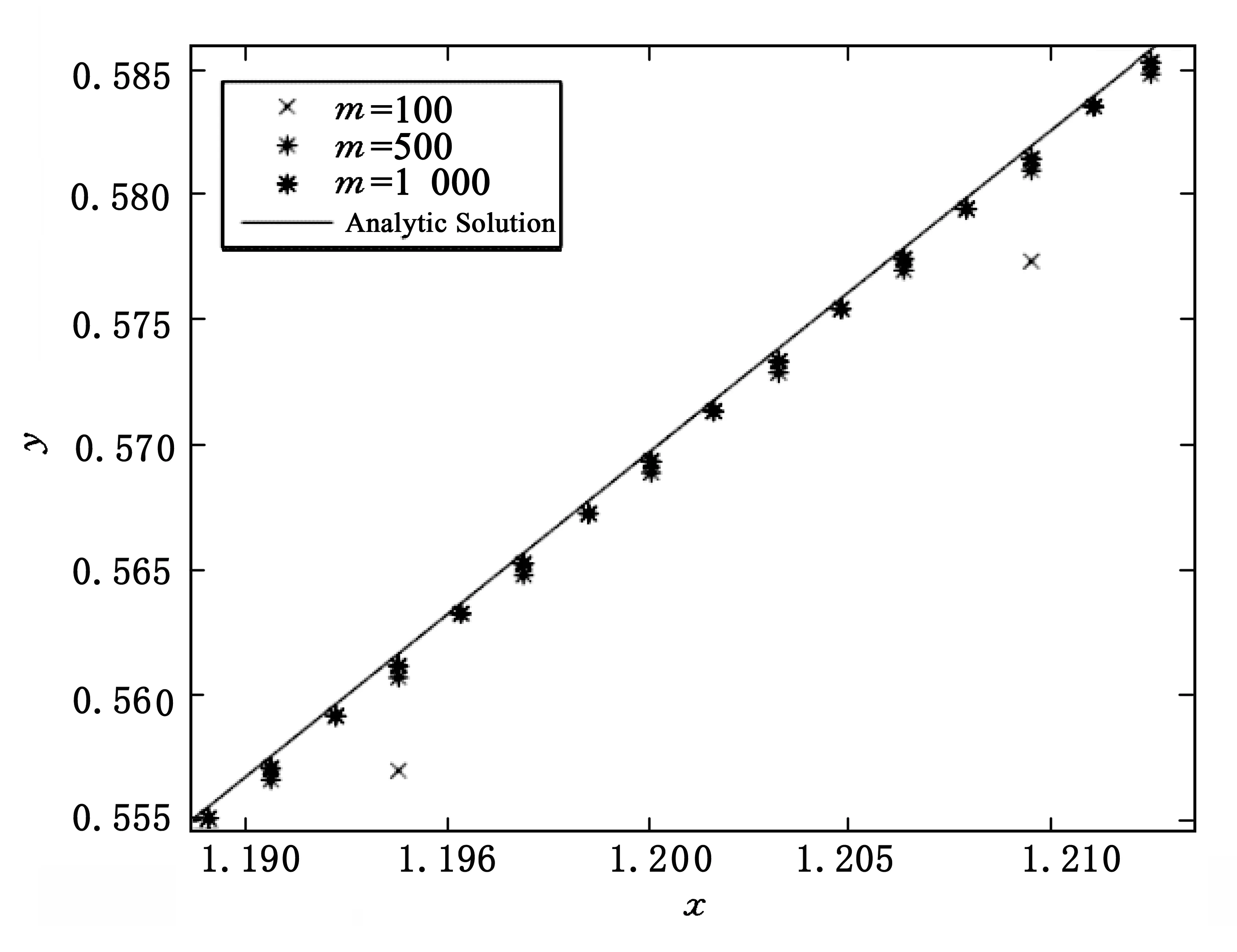
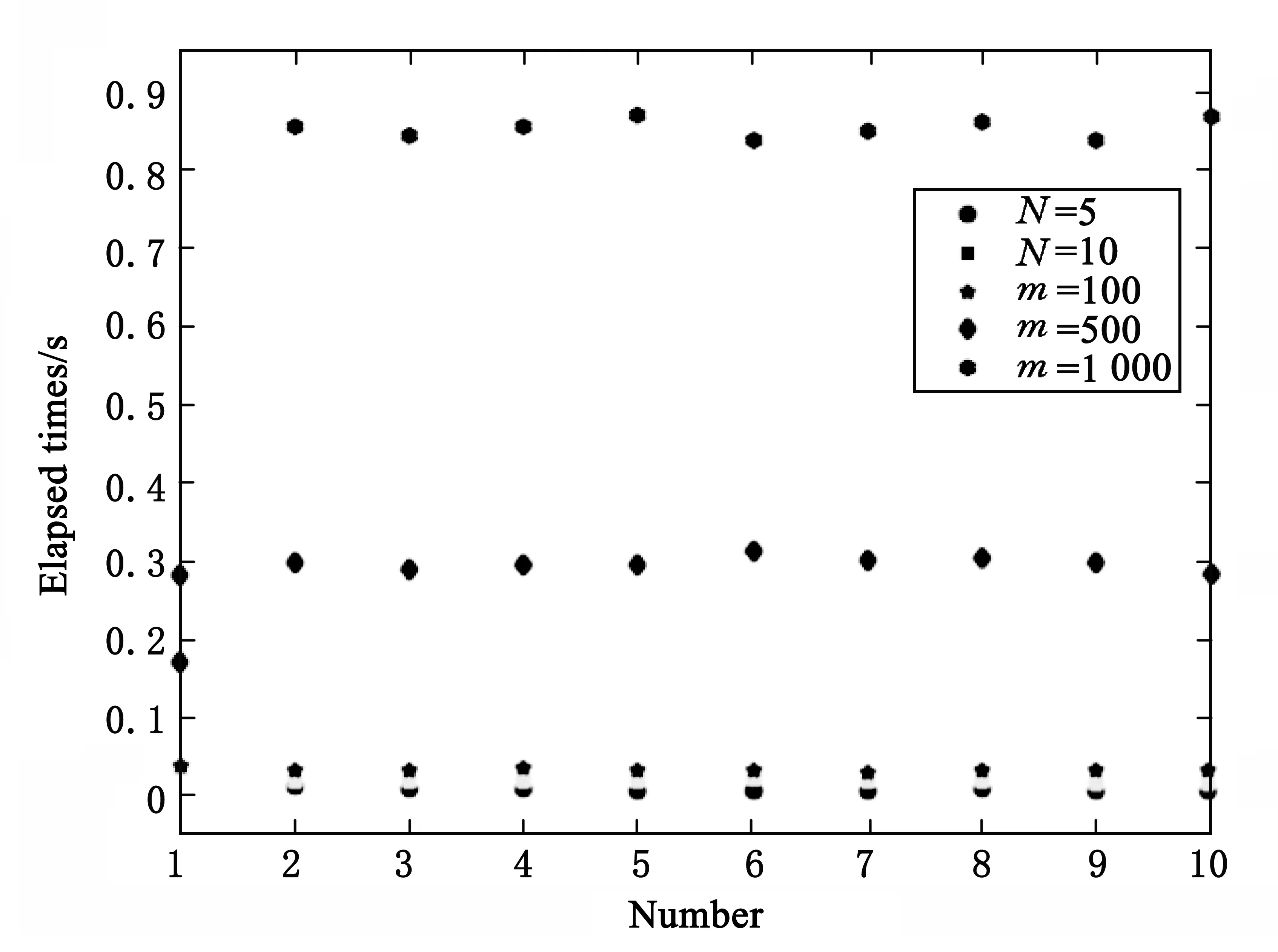
定理1[25]对任意连续函数y:[0,1]→R,存在函数ψ:[0,1]→R,基函数φi:[0,1]→[0,1](i=0,1,…,n)及常数0<ωi<1,0 (3) 且yA(x)是y(x)的近似解. 定理2[25]对任意连续函数y:[0,1]→R,有界函数ψ:[0,1]→R,及任意给定的ε>0,存在自然数N及实数ωi,vi,bi(i=1,2,…,n),使得 (4) 即 |y(x)-yA(x)|<ε. (5) 定理3假定y(x)是问题(2)的解析解,由定理1及定理2可知,存在yA(x)是y(x)的近似解. 证明:由定理1及定理2,很容易构造y(x)的近似解yA(x). 假定yA(x)是y(x)的近似解,且存在函数ψ:[0,1]→R,基函数φi:[0,1]→[0,1](i=0,1,…,n)及常数0<ωi<1,0 (6) 且 (7) (8) 求出式(6)在区间端点处的值yA(a),yA(b): (9) 假定yA(x)是问题(2)的解,则 (10) 将式(6-9)代入(10),可得: (11) 选择确定的激活函数φi及函数ψ,构造两点边值问题(2)的拓扑网络,这时方程(11)是权值参数ωi,vi,bi(i=1,2,…,n)的方程组,通过优化算法求出参数,就得到y(x)的近似解yA(x),即问题(2)的近似解. 选择合适的激活函数φi及函数ψ,可以将方程组(11)表示成矩阵形式: Hβ=T (12) 这里,矩阵H及T与权值参数ωi,vi,bi(i=1,2,…,n)无关,β只与ωi,vi,bi(i=1,2,…,n)有关. 由矩阵分析理论可知,当矩阵H为方阵,且是可逆矩阵时,式(12)存在唯一解β=H-1T,由得出的权值向量β,代入式(3)可得yA(x),此时yA(x)使得式(10)完全成立,是原问题(2)的准确解; 事实上,很多情况下,矩阵H不是方阵且不可逆,这时可以通过计算[26] (13) 定义1n×m阶矩阵H†是m×n阶矩阵H的广义逆矩阵,若满足 HH†H=H,H†HH†=H†,(HH†)T=HH†,(H†H)T=H†H, 由定义1可知,存在H†是H的广义逆矩阵,使得 (14) 使得式(13)成立. 算法步骤: 1)选择合适的激活函数φi及函数ψ,建立两点边值问题(2)的神经网络模型,构造近似解yA(x). 2)将yA(x)代入问题(2)得到方程(11). 3)将方程(11)表示成矩阵形式(12). 4)计算H†. 为了方便进行数值实验,这里近似解的构造采用Xu等[20]提出的方法,即 (15) 使用IELM算法计算权值参数an(n=0,1,…,N),bn(n=1,2,…,N). 例1求解线性边值问题 在区间0 由公式(15)构造该问题的近似解及神经网络模型,网络拓扑结构为1×(2N+1)×1,假定样本量为m,采用IELM算法计算权值参数.图1与图2表示网络拓扑结构及样本量对计算结果的影响,图3表示不同情况下计算10次,每次计算所需时间比较,表1及表2表示网络拓扑结构及样本量对计算精度及计算速度的影响. 图1 N取不同值时数值解与解析解 图2 样本量m取不同值时数值解与精确解 图3 不同情况下每次计算时间比较 NN=5N=10max(abs(yA-y))0.358 80.013 1t/s0.023 3980.015 812 注:t/s为统计计算10次的平均时间. 表2 N=10时,样本量m与算法性能之间的关系 注:t/s为统计计算10次的平均时间. 由表1实验数据可知,神经网络结构(即隐层神经元数量)对计算精度影响较大,对计算速度影响较小:当样本量固定时,N=10时误差最大值比N=5时降低了一位精度,平均计算时间少了0.007 586;由表2实验数据可知,样本量对计算精度及计算速度的影响均较大,当神经网络结构固定时,增加样本量,可以提高计算精度误差最大值减小,平均计算时间也快速增加. 例2求解线性边值问题 由公式(15)构造该问题的近似解及神经网络模型,网络拓扑结构为1×(2N+1)×1,假定样本量为m,采用IELM算法计算权值参数.计算结果如下:图4与图5表示网络拓扑结构及样本量对计算结果的影响,图6表示不同情况下计算10次,每次计算所需时间比较,表3及表4表示网络拓扑结构及样本量对计算精度及计算速度的影响. 图4 N取不同值时数值解与解析解 图5 样本量m取不同值时数值解与精确解 图6 不同情况下每次计算时间比较 NN=5N=10max(abs(yA-y))0.031 30.013 2t/s0.025 1860.019 834 注:t/s为统计计算10次的平均时间. 表4 N=10时,样本量m与算法性能之间的关系 注:t/s为统计计算10次的平均时间. 由表3实验数据可知,神经网络结构(即隐层神经元数量)对计算精度影响较大,对计算速度影响较小:当样本量固定时,N=10时误差最大值比N=5时降低0.018 1,平均计算时间少0.005 352.由表4实验数据可知,样本量对计算精度及计算速度的影响均较大,当神经网络结构固定时,增加样本量,可以提高计算精度误差最大值减小,平均计算时间也快速增加. 通过介绍求解一类线性微分方程两点边值问题的神经网络方法,建立该问题的神经网络模型.当近似解满足微分方程及边值条件时,根据矩阵分析理论,可以采用基于广义逆矩阵的IELM算法求解近似解中的权值,为一类线性微分方程两点边值问题的数值解提供一种新的方法.数值实验结果表明,采用IELM算法求解神经网络模型中的权值参数,计算精度及速度只与网络拓扑结构中隐层神经元数量及样本量有关,且只需少量的隐层神经元,通过增加样本量即可得到相应的计算精度.本文的实验结果可以为该方法在应用时隐层神经元及样本量的选择提供参考,未来可以研究该算法的推广能力,如隐层神经元及样本量的最优取值区间等. 参考文献: [1] 韩旭里.数值分析#:#Numerical Analysis[M].北京:高等教育出版社,2011. [2] LAGARIS I E,LIKAS A C.Artificial neural networks for solving ordinary and partial differential equations[J].IEEE Trans Neural Netw,1998,9(5):987-1000. [3] LI J Y,LUO S W,QI Y J,et al.Numerical solution of differential equations by radial basis function neural networks[J].Proc Int Jt Conf Neural Netw,2002,1:773-777. [4] NAM M D,THANH T C.Numerical solution of differential equations using multiquadric radial basis function networks[J].Neural Netw,2001,14:185-199. [5] CHUA L O,YANG L.Cellular neural networks:theory[J].IEEE Trans Circuits Syst,1988,35:1257-1272. [6] RAMUHALLI P,UDPA L,UDPA S S.Finite element neural networks for solving differential equations[J].IEEE Trans Neural Netw,2005,16(6):1381-1392. [7] LI X,OUYANG J,LI Q,et al.Integration wavelet neural network for steady convection dominated diffusion problem[J].IEEE Computer Society,2010,2(2):109-112. [8] MOODY J,DARKEN C J.Fast learning in networks of locally tuned processing units[J].Neural Comput,2002,35(10):1257-1272. [9] ESPOSITO A,MARINARO M,ORICCHIO D,et al.Approximation of continuous and discontinuous mappings by a growing neural RBF-based algorithm[J].Neural Netw,2000,13:651-665. [10] PARK J,SANDBERG I W.Approximation and radial basis function networks[J].Neural Comput,1993,5(2):305-316. [11] HAYKIN S.Neural networks:a comprehensive foundation[M].N.J.:Prentic Hall,1999. [12] FRANKE R.Scattered data interpolation:tests of some methods[J].Math Comput,1982,38(157):181-200. [13] NAM M D,THANH T C.Approximation of function and its derivatives using radial basis function networks[J].Neural Netw,2001,14:185-199. [14] NAM M D,THANH T C.Numerical solution of differential equations using multiquadric radial basis function networks[J].Neural Netw,2001,14:185-199. [15] MANGANARO G,ARENA P,FORTUNA P.Cellular neural networks:chaos,complexity and VLSI processing[M].Berlin:Springer,1999. [16] CHEDHOU J C,KYAMAKYA K,LATIF M A,et al.Solving stiff ordinary and partial differential equations using analog computing based on cellular neural networks[J].ISAST Trans Comput Intell Syst,2009,1(2):38-46. [17] TAKEUCHI J,KOSUGI Y.Neural network representation of the finite element method[J].Neural Netw,1994,7(2):389-395. [18] MEADE JR A J,FERNANDEZ A A.The numerical solution of linear ordinary differential equations by feedforward neural networks[J].Math Comput Model,1994,19:l-25. [19] MALL S,CHAKRAVERTY S.Application of legendre neural network for solving ordinary differential equations[J].Applied Computing,2016,43:347-356. [20] XU L Y,HUI W,ZENG Z Z.The Algorithm of Neural Networks on the Initial Value Problems in Ordinary Differential Equations[C].2007 2nd Conference on Industrial Electronics and Applications,2007:813-816. [21] TSOULOS I G,GAVRILIS D,GLAVAS E.Solving differential equations with constructed neural networks[J].Neurocomputing,2009,72:2385-2391. [22] REIDMILLER M,BRAUN H.A direct adaptive method for faster back propagation learning:the RPROP algorithm[J].IEEE International Conference on Neural Networks,1993,1(A8):586-591. [23] RUDD K,FERRARI S.A constrained integration (CINT) approach to solving partial differential equations using artificial neural networks[J].Neurocomputing,2015,155(C):277-285. [24] AARTS L P,VEER P V.Neural network method for partial differential equations[J].Neural Process Lett,2001,14:261-271. [25] BEIDOKHTI R S,MALEK A.Solving initial-boundary value problems for systems of partial differential equations using neural networks and optimization techniques[J].Franklin Inst,2009,346:898-913. [26] HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/2/3):489-501.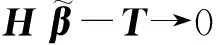
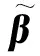
2 数值实验





3 结论
