一类三阶非线性系统的Lyapunov函数构造及稳定性

张永华

（安康职业技术学院 基础教学部，陕西 安康 725000）

非线性系统的稳定性分析是近代数学研究的一个新课题，能否构造出一个合适的Lyapunov函数，是分析系统稳定性的关键。本文利用Wall的能量度量算法构造一类非线性系统的Lyapunov函数，并得到零解的稳定性[1]。

1 Wall的能量度量算法

原新生等人用Wall的能量度量算法构造了一类三阶非线性系统的Lyapunov函数。Wall的能量度量算法简单概括为如下六个步骤[2]：

第一步，将所描述的系统改写成一阶联立的微分方程组

第二步，将改写的微分方程组写成如下形式

第三步，将式(1-2)写成如下形式

第四步，进行适当的代换和加法运算，将式(1-3)的微分方程组化为

第五步，构造函数

第六步，求出式(1-5)的全导数

由所求出的V(x)函数类型和(x)符号，再根据Lyapunov稳定性定理，则可以得出系统零解的稳定性。Wall的能量度量算法用来构造Lyapunov函数具有一定的适应性，但有时常常采用倒推的Wall的能量度量算法，具有很好的效果。

2 应用举例

例1 用Wall的能量度量算法讨论三阶非线性系统零解的稳定性[2]。

解 将其化为如下等阶形式

将式(2-1)变成如下形式

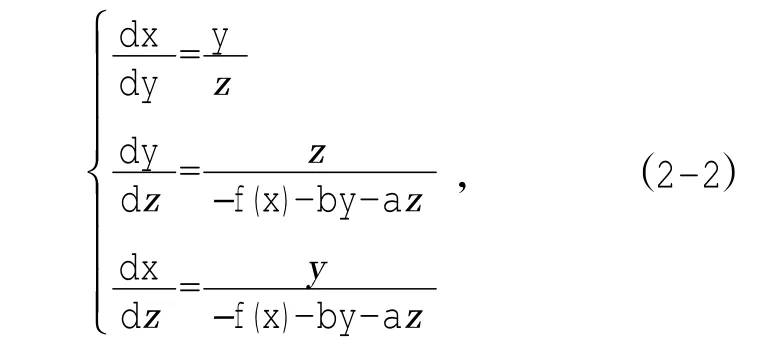
对式(2-2)进行适当变形得

将式(2-3)中的式(1)×a 代入到式(3)+ 式(2)得

按照Wall的能量度量算法构造函数

其中，

对式(2-5)求全导数得

因此可得出下列结论：

事实上，在定理条件下，只要证明V(x,y,)是正定函数，显然只要证明函数是正定的且具有无穷大性质即可。

证 显见，当y=0时，H(x,0)=F(x)具有此性质；当y≠0时，

因为

所以函数是正定的且具有无穷大的性质，从而定理得征。

例2 用Wall的能量度量算法讨论下列三阶非线性系统的稳定性[3]。

解 将系统(2-7)化为如下等阶形式

将式(2-8)变形为

将式(2-9)进行适当变形得

将式(2-10)中的式(1)代入式(3)+ 式(2)得

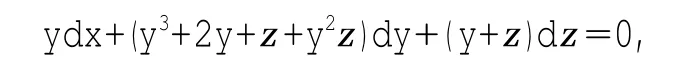
按照Wall的能量度量算法构造函数

对式(2-11)求全导数得

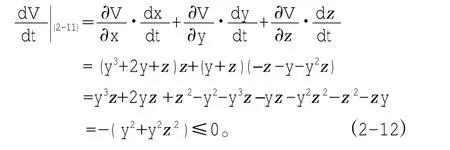
由于V(x,y,z)≥0是正定的，式(2-12)是负定的，因此系统(2-7)的零解是渐进稳定的，同时也是稳定的。

由例1、例2可看出，这两个非线性系统并不需要用“类比法”构造Lyapunov函数[4]，用Wall的能量度量算法构造的Lyapunov函数对得出系统稳定性更具有说明性。

[1]原新生，张怀涛.一类三阶非线性系统的李雅普诺夫函数构造[J].安阳师范学院学报，2011，13（5）：53-55.

[2]王联，王慕秋.一类三阶非线性系统李雅普诺夫函数构造之分析[J].应用数学学报，1983，7（3）：309-323.

[3]张永华.非线性系统的Lyapunov函数构造及稳定性[D].西安：西安建筑科技大学，2009.

[4]王联，王暮秋.论李雅普诺夫函数的构造[J].数学进展，1984，13 （2）：81-102.