一类平面分段光滑线性Hamilton系统在多项式扰动下的极限环个数

程振峰，李宝毅，张永康

（天津师范大学数学科学学院，天津300387）

1 引言和主要结果

分段光滑线性系统广泛应用于机械学、电子工程学和自动化理论等领域.为了估计2个区域的分段光滑线性Hamilton系统在扰动下的极限环个数，文献[1]证明了焦点-焦点型、焦点-抛物型和抛物-抛物型的分段线性系统至少存在2个极限环.文献[2]研究了分段多项式系统

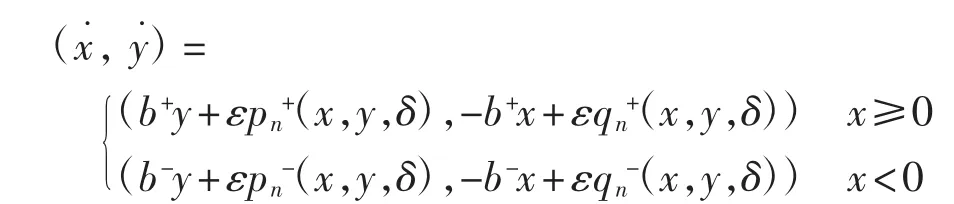
其中：b±＞0；和为任意n次多项式.证明了该系统最多存在n个极限环.文献[3]研究了分段光滑线性系统

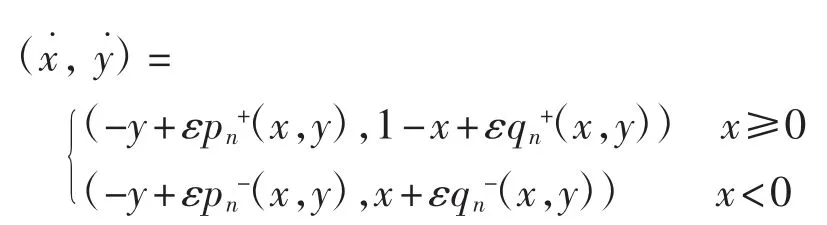
其中和为任意n次多项式.证明了该系统至少存在n+[（n+1）/2]个极限环.文献[4-5]分别构造了2种分段光滑二次系统，并证明了系统至少Hopf分支出5个和9个极限环.

本文研究分段光滑近Hamilton系统

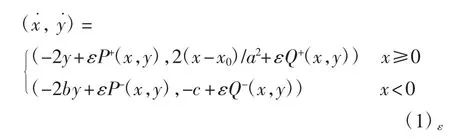
其中：a、b、c∈R+；x0∈R；0 ＜ ε≪1；n∈N+；

当ε=0时，（1）0的分段Hamilton函数为

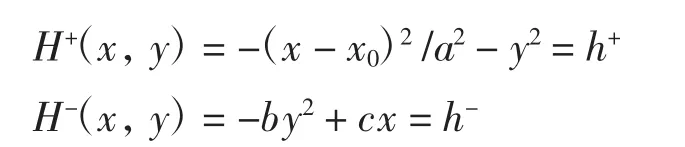
其中：；h-∈R-.此时分段光滑Hamilton系统（1）0存在逆时针走向的周期闭轨族，

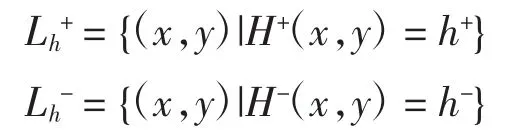
由于H+（x，y）关于x轴对称，故可设与负y轴的交点为A（0，-u），与正y轴的交点为A1（0，u），其中u=.对应的，故与正y轴的交点为A1（0，u），与负y轴的交点为 A（0，-u）.本文得到如下定理.

定理当x0=0时，系统（1）ε极限环个数的上界为n+[（n+1）/2]；当x0≠0时，系统（1）ε极限环个数的上界为n-1+2[（n+1）/2].

2 一阶Melnikov函数

设H+（x，y）=-v2，其中.设 α =arccos（-x0/av），则的参数方程可设为

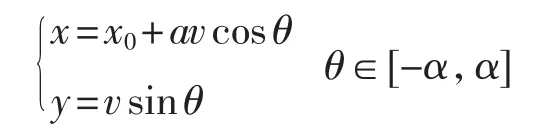
设的参数方程为

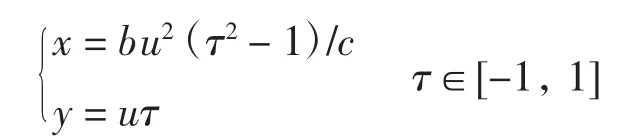
引理1[6]系统（1）ε的一阶Melnikov函数为

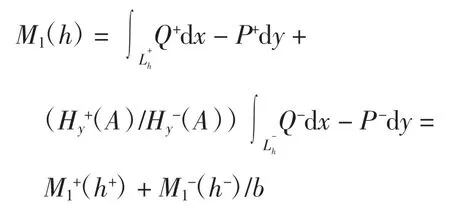
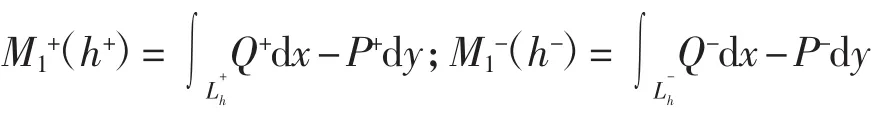
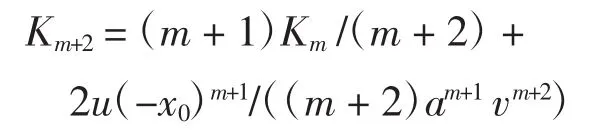
证明显然K0=2α，K1=2sin α=2u/v，则

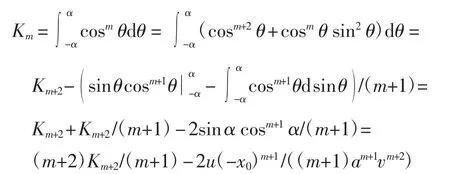
整理可得Km+2=（m+1）Km/（m+2）+2u（-x0）m+1/（（m+2）am+1·vm+2）.证毕.

命题1设ξ=[n/2]，η=[（n-1）/2]，当x≥0时，系统（1）ε的 Melnikov函数为

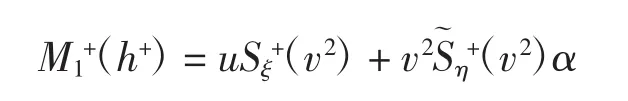
其中和分别表示关于v2的系数独立的ξ和η次多项式.

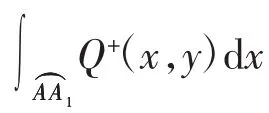
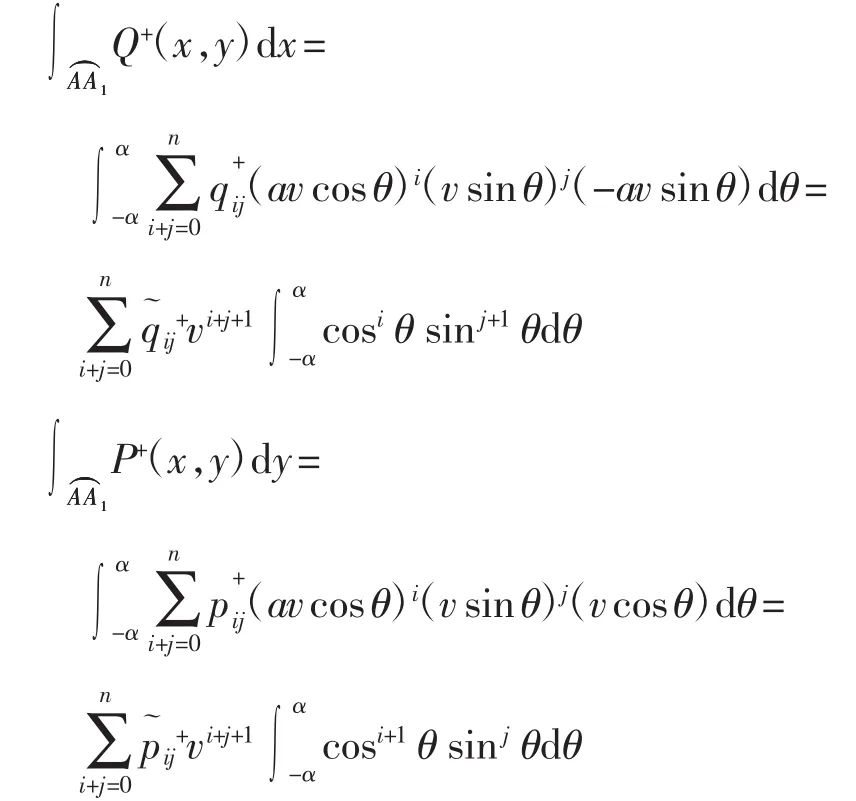
所以

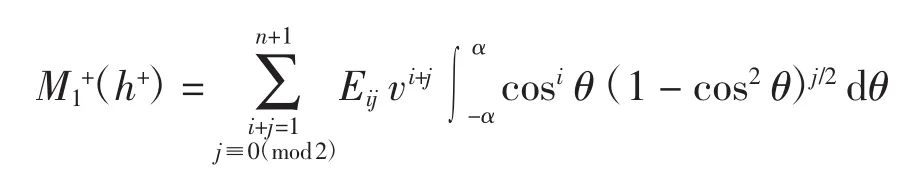
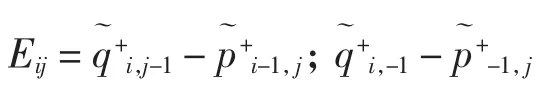
使用数学归纳法.当n=1时，

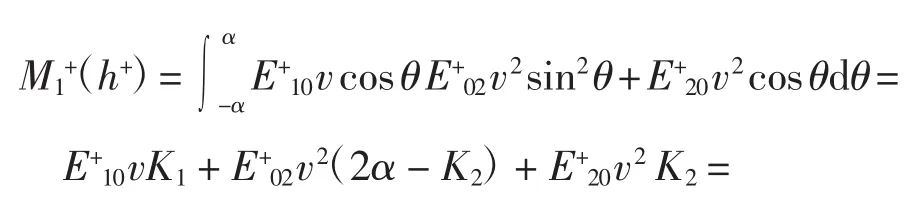
易知两项系数独立，满足命题1的结论.当n=2时，考虑增加项，有

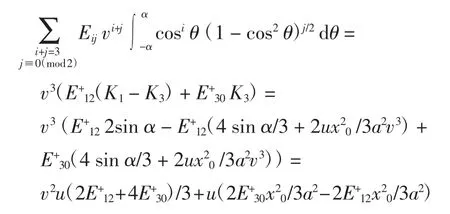
其中两项系数独立，满足命题1的结论.

假设当n=2k（k∈N*）时结论成立，则当n=2k+1时，有

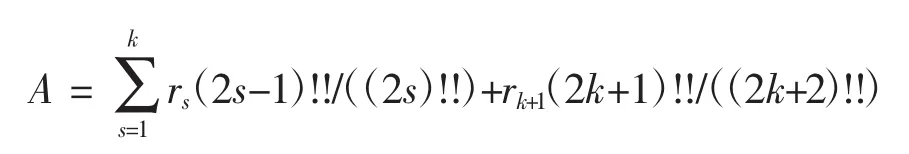
所以增加项为Av2k+2α，即当n=2k+1时命题1成立.

假设当n=2k+1（k∈N*）时结论成立，则当n=2k+2时，有

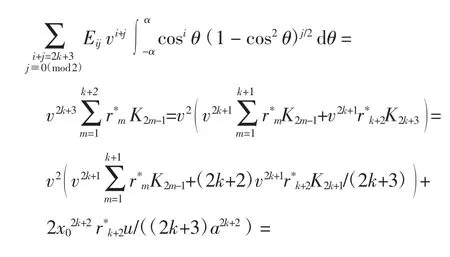
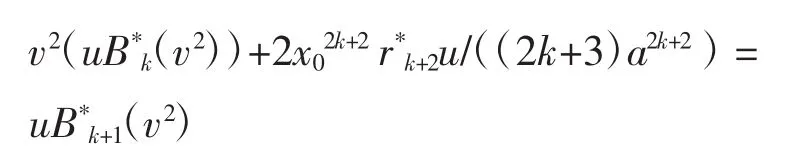
命题2当x＜0时，系统（1）ε的Melnikov函数为，其中为系数独立的u2的n次多项式，n∈N*.

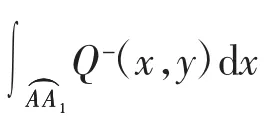
设，则有

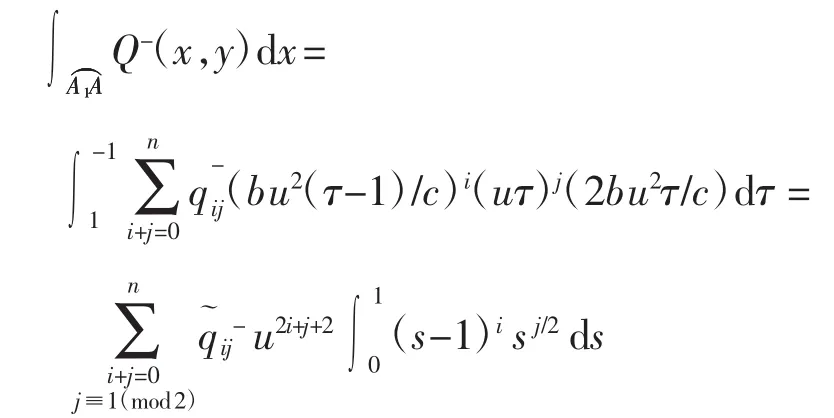
因为 3≤2i+（j+1）+1≤2i+2j+1=2n+1，所以

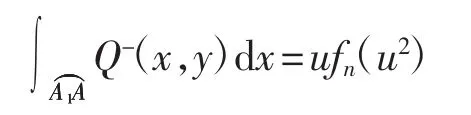
其中fn（u2）是关于u2的n次多项式，且n≥1.

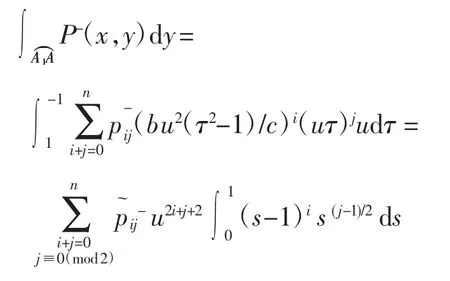
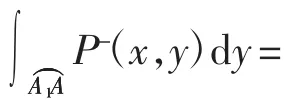
命题2得证.

3 定理的证明

由引理1、命题1和命题2可得系统（1）ε的一阶Melnikov函数为

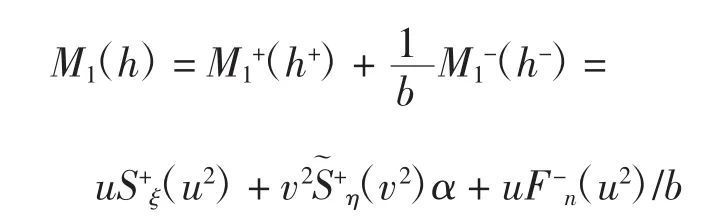
令，则

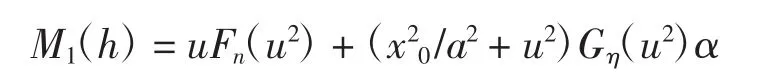
当x0=0时，α=π/2，因此M1（h）=u（Fn（u2）+uGη（u2）·π/2）.因为u＞0，所以M1（h）=0等价于Fn（u2）+uGη（u2）·π/2=0，设

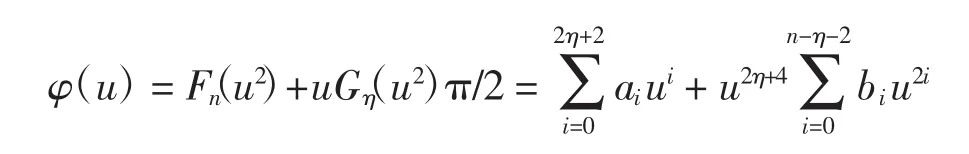
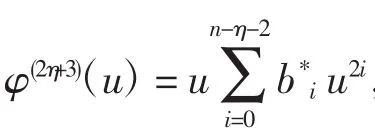
当x0≠0时，M1（h）=0等价于

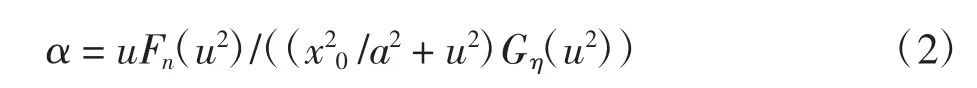
式（2）对u求导，整理后可得

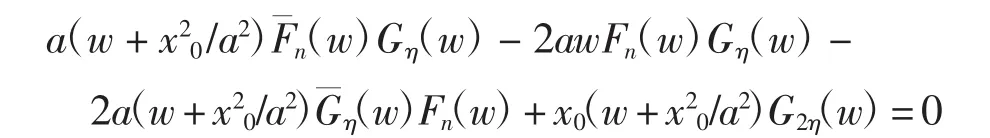
其中：.上面方程至多有n+η+1=n+[（n+1）/2]个零点.注意到式（2）右端分母至多有η个正零点，由文献[8]可得M1（h）至多存在n+2[（n+1）/2]个正零点.由于u＞0，且当u=0时M1（h）=0，所以M1（h）正零点个数的上界是n+2[（n+1）/2]-1.故当x0≠0时系统（1）ε极限环个数的上界是n+2[（n+1）/2]-1.

[1]HAN M A，ZHANG W N.On Hopf bifurcation in nonsmooth planar systems[J].JournalofDifferentialEquations，2010，248（9）：2399-2416.

[2]LIU X，HAN M A.Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems[J].International Journal of Bifurcation and Chaos，2010，20（5）：1379-1390.

[3]LIANG F，HAN M A，ROMANOVSKI V G.Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian systems with a homoclinic loop[J].Nonlinear Analysis，2012，75（11）：4355-4374.

[4]GASULL A，TORREGROSA J.Center-focus problem for discontinuous planar differential equations[J].International Journal of Bifurcation and Chaos，2003，13（7）：1755-1765.

[5]CHEN X W，DU Z D.Limit cycles bifurcate from centers of discontinuous quadratic systems[J].Computer Mathematics with Applications，2010，59（12）：3836-3848.

[6]LIANG F，HAN M A.Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth system[J].Chaos Solitons and Fractals，2006，28（4）：454-464.

[7]张蓉蓉，李宝毅，张永康.一类平面分段光滑二次系统的极限环个数[J].天津师范大学学报（自然科学版），2017，37（5）：7-10.ZHANG R R，LI B Y，ZHANG Y K.Number of limit cycles for a class of planar piecewise smooth quadratic systems[J].Journal of Tianjin Normal University（Natural Science Edition），2017，37（5）：7-10（in Chinese）.

[8]赵凌燕，李宝毅.罗尔定理的推广及其应用[J].天津师范大学学报（自然科学版），2016，36（4）：6-9.ZHAO L Y，LI B Y.Promotion of Rolle theorem and it′s application[J].Journal of Tianjin Normal University（Natural Science Edition），2016，36（4）：6-9（in Chinese）.