剪切波在堆石体中传播的细观数值模拟

杨尚慧 ，马刚 ，周伟 ，陈远 ，常晓林

(1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉，430072；2. 武汉大学 水工岩石力学教育部重点实验室，湖北 武汉 430072)

岩土颗粒材料的小应变剪切模量是岩土工程设计与分析中的重要力学参数之一[1−2]，被广泛应用于地震、爆破等土动力问题，以及分析一些土工结构物作用下地基土的静力变形中。土体的小应变剪切模量可通过现场试验和室内试验来测定[3−5]，包括下孔法、跨孔法以及表面波法等。室内试验则以共振柱和弯曲元试验为主，通过直接测定土体的剪切波速获得。自SHIRLEY等[6]采用弯曲元法测试室内制备高岭土试样的剪切波速和能量衰减特性，这项无损技术因原理明确、操作简单、价格低廉等优势，被广泛用于土体小应变剪切模量的测定[7−8]。弯曲元通常是由紧密粘结的2片或多片压电陶瓷晶体片组成，是一种可通过压电效应和逆压电效应实现机械能和电能之间转换的机电传感器[7]。进行土样剪切波速测试时，固定在装置一端的弯曲元元件作为激发元在脉冲电压下产生振动，激发出剪切波，固定在装置另一端的弯曲元元件作为接收元接收经土体传播而来的剪切波，并通过数据采集装置将接收元产生的振动转化为电信号，进而与激发元的电信号对比即可计算出土体的剪切波速。土体的剪切波速与众多因素密切相关，如颗粒形状、级配、孔隙比、应力水平和应力历史等[9−11]。ZENG等[12]通过弯曲元法测试了砂土在无侧向应变条件下不同应力面上的小应变剪切模量，提出了不同应力状态下小应变剪切模量的经验公式。吴宏伟等[13]利用弯曲元法研究了应力状态对上海原状黏土小应变剪切模量的影响，并进一步借助孔隙比函数建立起与土体应力状态的关系表达式。徐洁等[14]通过2组弯曲元试验研究了吸力和干湿路径对粉土小应变剪切模量的作用，并结合试验结果改进了小应变剪切模量半经验公式。采用弯曲元技术进行的剪切波试验时，如何准确地确定剪切波的传播时间，一直存在较大的争议。这是因为颗粒体系的内在复杂性、信号干扰(如串音、压缩波干预等)以及本身的组构缺陷[15−18]，可能产生30%~50%的测量误差[17]。目前，国内外学者利用离散元法与室内试验相结合，针对颗粒材料的波动问题开展了大量研究，克服了物理试验中的信号干扰问题，能够得到质量较高的剪切波接收信号[18−20]。徐晓敏等[18]针对无黏性颗粒材料进行了三轴试验离散元模拟，并设置激发源和接收源实现了颗粒材料中剪切波传播的模拟，系统分析了激发频率等诸多因素对剪切波速的影响。O′DONOVAN等[19]模拟了均匀圆盘的理想六角堆积体的二维弯曲元试验，比较了4种剪切波速的确定方法，并研究了离散元模型的细观参数与剪切波速的关系。NING等[20]对由球形颗粒随机堆积而成的圆柱体试样进行了三维弯曲元试验数值模拟，采用颗粒速度矢量场的演变表示波传播过程中的颗粒运动情况。MA等[21−24]提出了随机颗粒不连续变形方法，采用随机模拟技术产生凸多边形颗粒及其在空间中的分布，真实模拟了颗粒形态，将颗粒划分成有限个单元，允许颗粒发生变形，颗粒与颗粒之间的相互作用力通过虚拟的法向和切向弹簧和阻尼器来传递。本文作者基于随机颗粒不连续变形方法从堆石体颗粒位移演化以及频域分析方面研究了剪切波传播特性；采用3种方法确定剪切波速并与双轴压缩试验结果进行比较，从而得到较优的剪切波传播时间确定方法；系统地分析激发频率、激发幅值、颗粒接触刚度以及围压对剪切波速的影响。

1 弯曲元数值试验

1.1 数值试样

生成二维多边形颗粒及其在空间中的分布，再压缩成指定尺寸的试样，试样级配曲线如图1所示，孔隙率为0.135。试样长×宽为12 m×6 m，最大粒径dmax为 80 mm，dmax/dmin=4(其中，dmin为最小粒径)。定义颗粒的外接椭圆的长短径之比为颗粒的形状指标，长短径比在 1.4~1.6之间呈均匀分布。试样中共生成 10 217个颗粒，采用二阶四边形单元离散得到64 838个单元和243 520个节点。为了模拟室内弯曲元剪切波速测试装置，试样上下端为刚性板，四周用橡胶模包裹住，橡胶模上下端与刚性板分离，围压施加在橡胶模上。橡胶模的厚度取 2 mm，采用超弹性膜单元模拟橡胶模。

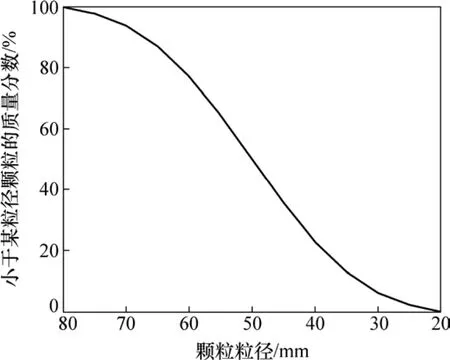
图1 数值试样级配曲线图Fig. 1 Particle size distribution of numerical sample

1.2 剪切波产生与传播

由于正弦波适用土样范围较广，而方波仅适用于刚度较小的土样[15]，本文采用正弦波作为激发信号。在试样顶部选取直径为0.75 m、厚度为0.20 m的薄层颗粒作为激发源，施加水平方向单周期正弦位移产生剪切波，与由单个颗粒作为激发源相比，薄层波源能够有效地减少物理试验中由压缩波和剪切波相互耦合形成的近场效应的干扰[15,20]。同时，沿试样轴线选取3个颗粒(R1，R2，R3)作为接收源，距离试样顶部的距离分别为6，9和12 m，并输出颗粒位移时程曲线，颗粒位移取颗粒上所有节点位移的平均值。数值试样如图2所示，模型主要计算参数如表1所示，所选参数可以保证基本消除弥散特性(λ/d50≥10，λ为波长；d50为颗粒平均粒径)与近场效应的影响(L/λ＞2，L为传播距离)[25−26]。

数值模拟开始时，先对试样施加围压进行等向固结，固结完成后对试样进行全约束继续运行一定时步，使得颗粒速度与激发幅值相比足够小，实现“除噪”。当试样中颗粒趋于平衡，对薄层激发源颗粒施加水平方向单周期正弦位移产生剪切波，侧向薄膜施加恒定围压，同时监测接收源颗粒水平方位移和竖直向坐标随时间变化动态。

图2 数值试样Fig. 2 Numerical sample

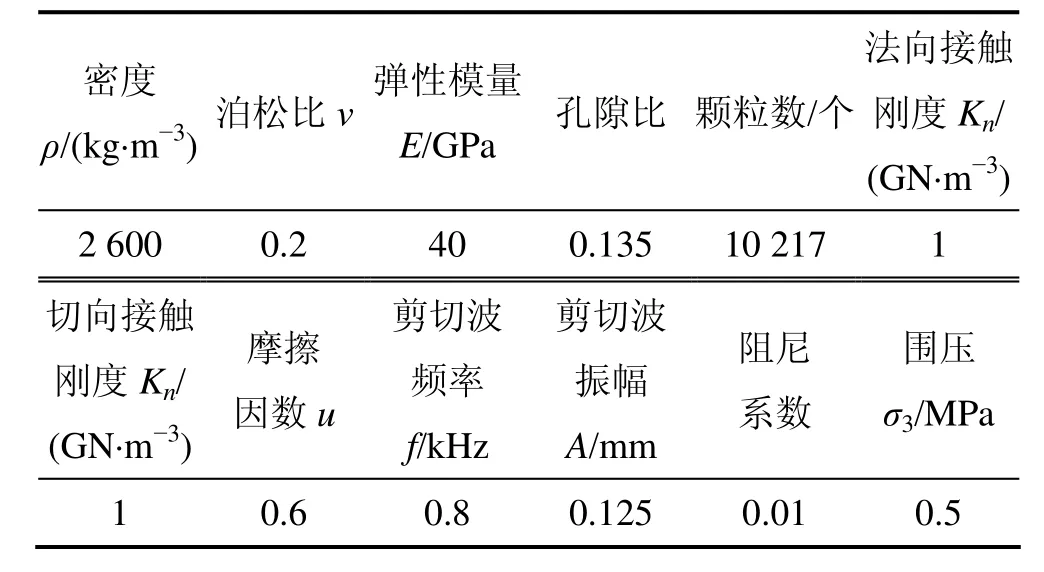
表1 计算参数Table 1 Parameters for calculation

2 数值模拟结果及分析

2.1 位移演化

图3所示为时间t为0和2T(T为施加的正弦位移的周期)时刻堆石体颗粒水平方向位移云图。从图3可以看出：在初始时刻，仅薄层颗粒产生位移，随着时间的推进，薄层颗粒的运动向下传递，且运动幅度逐渐降减弱，显示了波在堆石体中的传播过程。

图3 不同时刻堆石体颗粒位移云图Fig. 3 Contours of particle displacement for different time

图4所示为数值试样中激发源与接收源颗粒水平方向位移时程曲线，其中，S代表激发源颗粒，R1，R2和R3代表接收源颗粒。从图4可以看出：接收源颗粒按照距离波源的远近依次做出响应，且波动幅度逐渐衰减；接收源颗粒 R1初始出现与激发源相位相反的位移，这是由于近场效应压缩波(P波)传播速度大于剪切波(S波)速度，先期到达；随着传播距离的增加，近场效应减弱，R2和R3颗粒初始反相位位移现象逐渐消失。对于单个接收源颗粒而言，运动经历了初期衰减随后在0.04~0.05 s间再次增强的过程，这是由底部刚性板边界的反射造成的。综合考虑剪切波传播过程中的近场效应以及由于阻尼等因素引起的振幅衰减所造成的影响，选取接收源颗粒 R1位移随时间变化曲线作为确定剪切波速的依据。

2.2 频域分析

频域分析方法又被称为快速傅里叶变换(fast Fourier transform, FFT)分析法，通过对获取的波信号数据进行快速傅里叶变换，将时域信号转变为频域信号，并对其时域和频域特性进行分析。为了更加精确地比较发射信号和接收信号的各频率组分，分别对其进行快速傅里叶变换，由于接收信号振幅衰减明显，与发射信号相差较大，不便于比较，因此，将接收信号振幅扩大20倍，结果如图5所示。

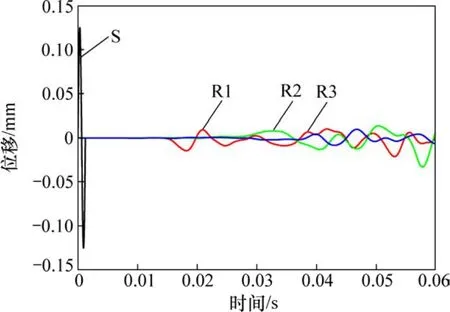
图4 输入接收信号波形图Fig. 4 Signals transmitted and received by bender element

图5 0.8 kHz发射信号与接收信号频域对比Fig. 5 Comparison between input signals and received signals in frequency domain for 0.8 kHz

由图5可知：堆石体颗粒对高频率剪切波信号具有明显的过滤作用。对于发射信号而言，单周期正弦波具有较宽的频率范围，最高频率达到1.6 kHz附近，峰值振幅对应的频率为0.8 kHz，而接收信号所包含的频率范围较窄，主要集中在1 kHz以下，最高频率大约在1.1 kHz附近；当频率大于0.5 kHz时，振幅迅速衰减，峰值振幅对应 3组频率分别为 0.12，0.15和0.18 kHZ。改变发射信号的频率，分别进行正弦位移频率为0.4，0.6和1 kHz的数值试验，并对发射信号和接收信号进行快速傅里叶变换，结果如图6所示。

由图5和图6可知：随着发射信号频率的增加，其所包含的频率范围也随之增大，峰值振幅对应的频率分别为0.4，0.6和1.0 kHz，而接收信号的频率范围与发射信号的频率无关，主要集中在1.0 kHz以下部分，并且当接收信号的频率大于0.5 kHz时，其对应的振幅将迅速减小。定义位移振幅趋于0 mm时对应的频率为堆石体振幅衰减的临界频率，计算得到不同发射信号频率下振幅衰减的临界频率的方差为3.2×10−5，说明其随发射信号频率变化不明显，证明临界频率是与试验参数无关的堆石体自身的特性参数。

图6 发射信号与接收信号频域对比Fig. 6 Comparison between input signals and received signals in frequency domain for different input signals

3 剪切波传播时间的确定

剪切波速由发射源和激发源的距离和剪切波的传递时间来确定，目前有2类确定剪切波传播时间的方法：直接确定法和计算分析法。直接确定法根据输入波形和输出波形的特征点确定传播时间，常见的有初达波法(S-S法)和峰值-峰值法(P-P法)，计算法通过互相关分析确定传播时间。分别根据S-S法、P-P法和互相关分析法薄层颗粒S和R1接收源颗粒位移波形曲线(见图7)确定颗粒体的剪切波速，并与双轴压缩试验结果进行对比，从而选择出较优的剪切波传播时间确定方法。

图7 剪切波传播时间的确定Fig. 7 Determination of travel time of shear wave

3.1 初达波法(S-S法)

初达波法利用剪切波的首次到达来确定传递时间，通常是以接收信号的首个偏转点作为剪切波的到达位置。发射弯曲元在激发剪切波的同时也产生压缩波，由于压缩波在土体中的传播速度比剪切波的大，将会引起接收信号产生初始位移而随后到达的剪切波将会改变波信号的方向，因此，将A′点视为剪切波到达接收源颗粒R1的初始位置，对应的时间为 18.288 ms，此时颗粒与薄层底部的距离为5.780 63 m，计算得到剪切波速为316.09 m/s。

3.2 特征点法(P-P法)

特征点法分别选取发射信号和接收信号的首个峰值点，通过峰值点间的时间和位移差来计算剪切波速，由图7可知：接收源颗粒R1位移波形的第1峰值B′对应的时间为20.603 ms，此时颗粒与薄层底部的距离为5.780 59 m，计算得到剪切波速为280.57 m/s。与初达波法相比，特征点法中接收信号的峰值点由于不受噪音干扰能够被清楚识别，但对选择首个峰值点还是最大峰值点问题仍存在一定争议[27]。

3.3 互相关法

初达波法和特征点法中均需要人为判断剪切波到达和传播时间，具有一定的主观性，而互相关法是一种数学方法，通过互相关函数即CXY来衡量2个信号之间的相关性，其数学表达式为

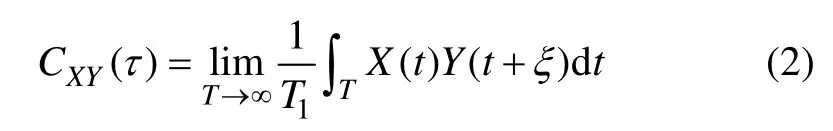
式中：T1为信号总测试时间；ξ为2个信号之间的时间差。

对发射信号和接收信号进行快速傅里叶变换得到如图8所示的互相关函数，取CXY最大值对应的时间tc作为剪切波的传播时间，得到tc=19.015 ms，计算得到剪切波速为299.91 m/s。

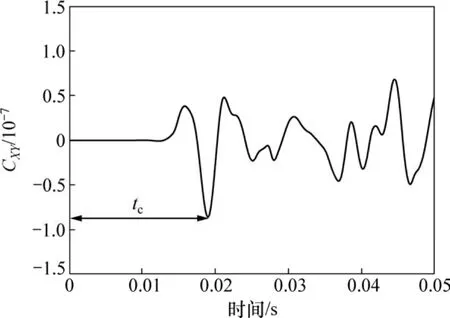
图8 互相关法确定剪切波到达时间Fig. 8 Determination of arrive time using cross-correlation method

3.4 剪切波速对比

进行双轴压缩试验得到小应变剪切模量Gmax，并进一步根据Gmax=ρvs2(其中，ρ为颗粒密度；vs为剪切波速)，计算剪切波速vs作为参照。双轴压缩试验与弯曲元试验采用相同的边界条件，均保持恒定围压，并将顶部刚性板按照1 kHz频率施加6级往复荷载，根据由6个循环荷载级的轴向动应力幅值σd和轴向动应变幅值εd绘制的σd−εd曲线的初始斜率计算得到数值试样的动弹性模量Emax=448.38 MPa，根据公式Gmax=Emax/2(1+v)最终得到vs的参考值为292.93 m/s。

将3种方法计算得到的剪切波速与双轴压缩试验参考值进行比较，如表2所示。从表2可以看出：采用互相关法计算得到的剪切波速与双轴试验结果最接近，说明基于随机颗粒不连续变形SGDD方法的堆石体二维弯曲元试验的数值模拟中，采用互相关法确定的剪切波传播时间精确度最高，与AHN等[28]基于离散元方法得到的结论相一致，因此，本文选择互相关分析作为计算剪切波传播时间的方法。

表2 不同计算方法剪切波速对比Table 2 Comparison of values of vs calculated by different methods

4 剪切波传播影响因素分析

堆石体中剪切波的传播受诸多因素的影响，主要包括激发幅值、激发频率、围压以及细观层次上的颗粒间接触刚度。

4.1 激发幅值

由于堆石体的剪切刚度是随应变水平变化的函数，因此剪切波速在不同的应变水平下有所不同。弯曲元试验中试样产生的剪切应变则是通过激发幅值来控制。分别进行A/d50=1×10−6~1×10−2(其中，A代表激发幅值)的6组平行试验，计算得到6种情况下的剪切波速如图9所示，同时提取出剪切波传播过程中接触失效率随时间变化曲线如图10所示。由图9可知：随着A/d50减少，剪切波速略有增加，当激发幅值小于10−3时，剪切波速趋于收敛，基本稳定。对应图10中的接触失效率变化曲线，当A/d50小于 10−3时，颗粒接触失效率的变化曲线近似重合，而当A/d50大于10−3时，接触失效率曲线上升，对应的剪切波速略有降低。

图9 激发幅值对剪切波速的影响Fig. 9 Influence of excitation amplitude on shear wave velocity

图10 不同激发幅值下接触失效率Fig. 10 Percentage of sliding contacts for different excitation amplitudes

4.2 激发频率

图11所示为激发频率分别为0.4，0.6，0.8和1.0 kHz时接收源颗粒R1输出的位移波形图。从图11可以看出：当激发频率小于0.6 kHz时，接收源颗粒的位移波形较微弱；当激发频率达到0.8 kHz后，信号强度增强并且波形相似，但1.0 kHz下波形振幅略有下降，即当激发频率为0.8 kHz时，接收信号振幅达到峰值，对应堆石体颗粒以最大振幅做振动。又由图5和图 6可知：接收信号包含的频率主要集中在0.8 kHz以下，因此，可近似认为0.8 kHz为堆石体的共振频率。另外，从图11还可以直接观察到不同频率下剪切波的初达时间，从而确定剪切波速，进一步得出当激发频率从0.4 kHz增加到0.8 kHz时，剪切波速略有增大；当激发频率达到共振频率后，剪切波速将保持稳定。

堆石体的强度部分来源于堆石体颗粒间摩擦的激励，为研究堆石体颗粒接触处的摩擦特性，定义堆石体颗粒摩擦激励指标为Im=|ft|/(fntanφ)(其中，ft和fn分别表示堆石体颗粒间切向接触力和法向接触力)。图12所示为不同激发频率下堆石体平均摩擦激励指标Im的演化曲线(Im为相应积分点对应的堆石体中所有接触处的平均摩擦激励)。从图12可以看出，初始阶段0.4 kHz和0.6 kHz激发频率下堆石体的摩擦激励系数演化曲线位于0.8 kHz和1 kHz曲线下方，当激发频率大于0.8 kHz时，曲线近似重合，对应图11中当激发频率小于共振频率时，堆石体响应较微弱，当激发频率达到共振频率后，响应增强并且波形相似。同时，随着波的传播，不同激发频率下堆石体的摩擦激励系数最终稳定在同一数值附近，对应堆石体的剪切波速随激发频率波动较小，稳定在1个定值附近。

图11 不同激发频率下接收波形Fig. 11 Waveform of a receiver in the time domain,excited by different frequencies

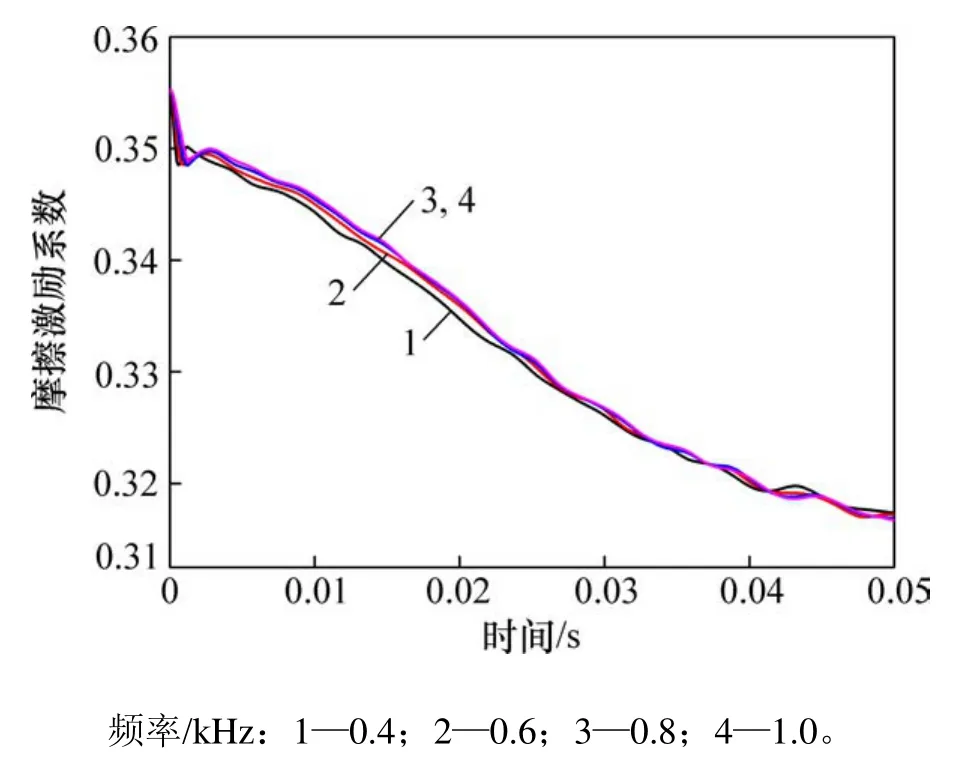
图12 不同激发频率下摩擦激励系数演化过程Fig. 12 Evolution of friction incentive index, excited by different frequencies

4.3 围压

堆石体的应力状态通过影响堆石体颗粒间的刚度从而使剪切波速发生改变，分别计算堆石体颗粒在0.4，0.5，0.6，0.8和1.0 MPa围压固结下的剪切波速，结果如图13所示。从图13可以看出：随着围压的增加，剪切波速逐渐增大，且低围压下的增加速度略大于高围压下的增加速度，即随着体系压强的增大，颗粒之间的接触更加紧密，对应的平均接触数增加，颗粒体系内部结构更不容易发生调整，相应的剪切波速增加速度降低。这与徐小敏等[18]得到的剪切波速随围压变化的基本规律一致，但剪切波速增长速度的变化仍存在差异，造成的原因可能是堆积方式以及填充率不同。

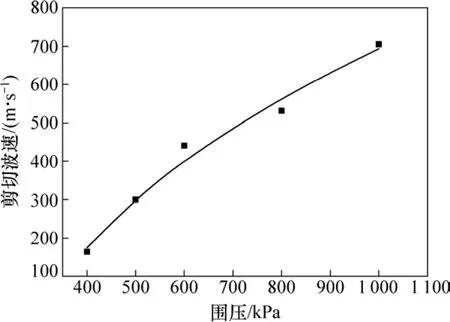
图13 围压对剪切波速的影响Fig. 13 Influence of confining pressure on shear wave velocity

4.4 颗粒接触刚度

堆石体的细观数值试验采用基于罚函数的线性接触模型，即通过法向和切向弹簧来传递堆石体颗粒间的法向和切向相互作用力，因此，需要堆石体颗粒间接触刚度作为细观参数。而在该接触模型中，接触刚度并没有明确的物理意义，也很难通过常规试验获取，因此，本文计算堆石体的法向接触刚度Kn分别取值1×105，5×105，1×106，5×106和 1×107kN/m3时的剪切波速，对其进行敏感性分析，如图14所示。由图14可知：剪切波速随法向接触刚度的增大而增加，并与法向接触刚度的开方近似成直线关系。DONOVAN等[19]采用离散元法模拟二维弯曲元试验也得到了相似的剪切波速与颗粒接触刚度之间的关系。

图14 颗粒接触刚度对剪切波速的影响Fig. 14 Influence of inter-particle contact spring stiffness on shear wave velocity

5 结论

1)堆石体颗粒对高频率的剪切波信号具有过滤作用，接收信号相对于发射信号而言包含的频率范围变窄，主要集中在1 kHz以下，并且振幅衰减的临界频率是与试验参数无关的堆石体自身的特性参数。

2)与初达波法和特征点法相比，互相关法计算得到的剪切波速与双轴压缩试验结果最接近，进一步验证了将其作为确定剪切波传播时间方法的合理性。

3)堆石体颗粒中剪切波的传播受诸多因素的影响，其中，随着激发幅值减少，剪切波速略有增加，当A/d50小于10−3时，剪切波速趋于收敛，基本稳定；当激发频率小于共振频率时，接收源颗粒的位移波形较微弱，且剪切波速随频率略有增加，当激发频率达到共振频率后，信号强度增强并且波形相似，同时剪切波速将保持稳定；随围压增加，剪切波速逐渐增大；剪切波速随法向接触刚度的增大而增加，并与法向接触刚度的开方近似成直线关系。

[1]CLAYTON C R I. Stiffness at small strain: research and practice[J]. Géotechnique, 2011, 61(1): 5−37.

[2]SANTAMARINA J C, KLEIN A, FAM M A. Soils and waves:Particulate materials behavior, characterization and process monitoring[J]. Journal of Soils and Sediments, 2001,1(2): 130−130.

[3]KOKUSHO T. Cyclic triaxial test of dynamic soil properties for wide strain range[J]. Soils & Foundations, 1980, 20(2): 45−60.

[4]BENEDETTO H D, EZAOUI A. Experimental measurements of the global anisotropic elastic behaviour of dry Hostun sand during triaxial tests, and effect of sample preparation[J].Géotechnique, 2009, 59(7): 621−635.

[5]CHAUDHARY S K. Measurement of quasi-elastic stiffness parameters of dense Toyoura sand in hollow cylinder apparatus and triaxial apparatus with bender elements[J]. Geotechnical Testing Journal, 2004, 27(1): 1−13.

[6]SHIRLEY D J, HAMPTON L D. Shear-wave measurements in laboratory sediments[J]. The Journal of the Acoustical Society of America, 1978, 63(2): 607−613.

[7]陈云敏, 周燕国, 黄博. 利用弯曲元测试砂土剪切模量的国际平行试验[J]. 岩土工程学报, 2006, 28(7): 874−880.CHEN Yunmin, ZHOU Yanguo, HUANG Bo. International parallel test on the measurement of shear modulus of sand using bender elements[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 874−880.

[8]FONSECA A V D, FERREIRA C, FAHEY M. A framework interpreting bender element tests, combining time-domain and frequency-domain methods[J]. Geotechnical Testing Journal,2009, 32(2): 91−107.

[9]周燕国. 土结构性的剪切波速表征及对动力特性的影响[D].杭州: 浙江大学建筑工程学院, 2007: 95−116.ZHOU Yanguo. Shear wave velocity-based characterization of soil structure and its effects on dynamic behavior[D]. Hangzhou:Zhejiang University. College of Civil Engineering and Architecture, 2007: 95−116.

[10]HARDIN B O, RICHART F E. Elastic wave velocities in granular soils[J]. Journal of the Soil Mechanics & Foundations Division, 1963, 89: 33−66.

[11]SUITS L D, SHEAHAN T C, PATEL A, et al. An empirical relationship for determining shear wave velocity in granular materials accounting for grain morphology[J]. Geotechnical Testing Journal, 2009, 32(1): 1−10.

[12]ZENG X, NI B. Stress-induced anisotropic G max of sands and its measurement[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(9): 741−749.

[13]吴宏伟, 李青, 刘国彬. 利用弯曲元测量上海原状软黏土各向异性剪切模量的试验研究[J]. 岩土工程学报, 2013, 35(1):150−156.WU Hongwei, LI Qing, LIU Guobin. Measurements of small-strain inherent stiffness anisotropy of intact Shanghai soft clay using bender elements[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 150−156.

[14]徐洁, 周超. 干湿路径影响粉土小应变剪切模量的试验研究[J]. 岩土力学, 2015: 36(1): 577−381.XU Jie, ZHOU Chao. Experimental study of effect of wetting-drying path on small-strain shear modulus of silt[J].Rock and Soil Mechanics, 2015: 36(1): 577−381.

[15]LEE J S, SANTAMARINA J C. Bender elements: performance and signal interpretation[J]. Journal of geotechnical and geoenvironmental engineering, 2005, 131(9): 1063−1070.

[16]ALVARADO G, COOP M R. On the performance of bender elements in triaxial tests[J]. Géotechnique, 2012, 62(1): 1−17.

[17]ARROYO M, MUIR WOOD D, GREENING P D. Source near-field effects and pulse tests in soil samples[J]. Géotechnique,2003, 53(3): 337−345.

[18]徐小敏, 凌道盛, 黄博, 等. 离散元模拟中颗粒材料剪切波速的剪切振动确定方法[J]. 岩土工程学报, 2011, 33(9):1462−1468.XU Xiaomin, LING Daosheng, HUANG Bo, et al.Determination of shear wave velocity in granular materials by shear vibration within discrete element simulation[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1462−1468.

[19]O’DONOVAN J, O’SULLIVAN C, MARKETOS G.Two-dimensional discrete element modelling of bender element tests on an idealised granular material[J]. Granular Matter, 2012,14(6): 733−747.

[20]NING Z, KHOUBANI A, EVANS T M. Shear wave propagation in granular assemblies[J]. Computers & Geotechnics, 2015, 69:615−626.

[21]MA G, ZHOU W, CHANG X L, et al. Combined fem/dem modeling of triaxial compression tests for rockfills with polyhedral particles[J]. International Journal of Geomechanics,2014, 14(4): 04014014.

[22]MA G, ZHOU W, CHANG X L. Modeling the particle breakage of rockfill materials with the cohesive crack model[J].Computers & Geotechnics, 2014, 61(61): 132−143.

[23]MA G, ZHOU W, NG T T, et al. Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage

model[J]. Acta Geotechnica, 2015, 10(4): 481−496.

[24]MA G, ZHOU W, CHANG X L, et al. Formation of shear bands in crushable and irregularly shaped granular materials and the associated microstructural evolution[J]. Powder Technology,2016, 301: 118−130.

[25]TOOMEY A, BEAN C J. Numerical simulation of seismic waves using a discrete particle scheme[J]. Geophysical Journal International, 2000, 141(3): 595−604.

[26]CHANEY R C, DEMARS K R, PENNINGTON D S, et al.Horizontally mounted bender elements for measuring anisotropic shear moduli in triaxial clay specimens[J]. Geotechnical Testing Journal, 2001, 24(2): 133−144.

[27]LEONG E C. Measuring shear wave velocity using bender elements[J]. Astm Geotechnical Testing Journal, 2005, 28(5):488−498.

[28]AHN J, BISCONTIN G, ROESSET J M. Wave propagation in nonlinear one-dimensional soil model[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2010,33(33): 487−509.