行波效应对连续刚构桥地震响应的研究

叶刘克

(安徽省七星工程测试有限公司，安徽 合肥 230000)

1 概述

大跨度桥梁结构的抗震问题一直备受关注，由于大跨度桥梁各支撑相距较远，导致地震波在传播过程中到达各支撑点的时间必然会存在一定差异[1-3]，而这种时间上的差异就称为行波效应。

在进行大跨度桥梁结构抗震研究时，若仅对大跨度桥梁进行一致地震输入，而忽略这种时间上的差异可能会引起结构的不安全，因此在进行大跨度桥梁抗震设计时不能单一考虑一致地震输入，而需要进行多点激励或非一致激励[4]。

2 工程背景

桥址位于渭北黄土台塬及沟壑区，地形起伏，线路行进在黄土台塬地段，途经地区冲沟较发育，主桥(97+2×180+97)m加劲钢桁连续刚构主跨分别跨越司家沟和漠谷河两条大型黄土冲沟，无常年流水。漠谷河大里程侧为阶形台地，地形较缓。桥址处地震动峰值加速度值为0.15g，桥址区场地类别为Ⅱ类[5]。

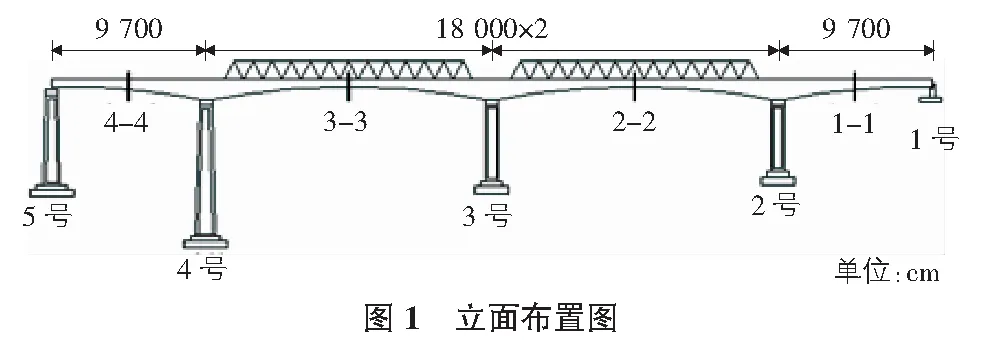
(97+2×180+97)m加劲钢桁连续刚构，主梁采用单箱双室变高度箱形截面，边跨及中跨梁高4.8 m，中支点处梁高12.5 m，梁高按1.6次抛物线变化，主梁中跨跨中40 m为等截面，梁高4.8 m。加劲钢桁为无竖杆三角形桁，整体式节点，中跨156 m范围内设置加劲钢桁，节间长度12.0 m，主桁中心距11.0 m，桁高12.0 m。该桥立面布置图如图1所示。

3 有限元模型

本桥以MIDAS软件进行计算，根据结构特点，全桥共划分为305个节点，337个单元，2号～4号墩顶刚性连接，承台底固结，模型如图2所示。

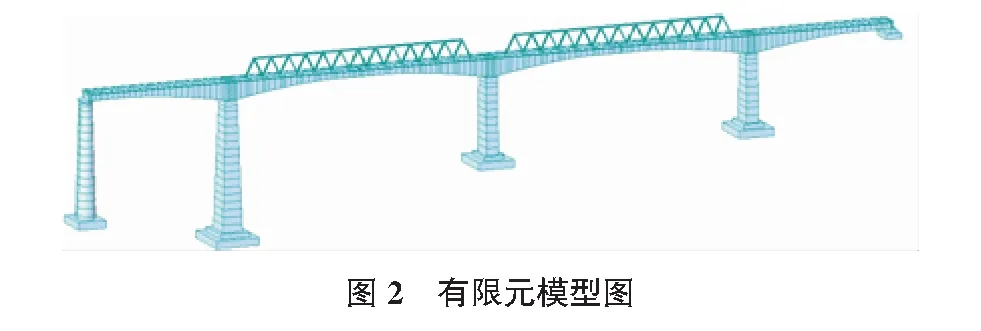
4 行波效应分析

由于行波效应的存在，地震波到达相邻承台底必然会有一定的时间差，因此，就需要对此类桥梁考虑多点激励问题。

4.1 视波速的选取及滞后时间计算

为了研究行波效应对桥梁结构的影响，选取视波速为200 m/s,300 m/s,400 m/s,500 m/s,800 m/s,1 200 m/s,1 800 m/s，并与一致激励进行对比，视波速及地震波到达各承台底支撑点的滞后时间如表1所示。

表1 视波速及承台底激励滞后时间

4.2 地震波纵向作用

选取Fernando波沿顺桥向进行输入，假设地震波从1号墩向5号墩传播。

4.2.1 不同波速下位移对比分析

根据理论计算模型，提取1号～5号墩墩顶纵向位移及主要控制截面1-1截面～4-4截面纵向位移如表2，表3所示。

表2 不同波速下各墩顶纵向位移(一)

表3 不同波速下主要控制截面纵向位移(一)

由表2，表3可知：1)当视波速较小时，墩顶及主要控制截面的纵向位移大于一致激励下的纵向位移。2)当波速为300 m/s时，2号墩～5号墩墩顶最大纵向位移分别是一致激励下纵向位移的1.14倍、1.45倍、1.41倍和1.23倍。3)当波速为300 m/s时，1-1截面～4-4截面最大纵向位移分别是一致激励下纵向位移的1.17倍、1.24倍、1.31倍和1.27倍。4)因此进行地震反应分析时，从位移角度来看仅考虑一致激励，结构是偏于不安全状态的。

4.2.2 不同波速下内力对比分析

根据理论计算模型，提取1号～5号墩墩顶弯矩及主要控制截面1-1截面～4-4截面弯矩作为重点考察的量值，如表4，表5所示。

表4 不同波速下墩底弯矩My(一)

表5 不同波速下主要控制截面弯矩My(一)

由表4,表5可知：1)当视波速较小时，墩底及主要控制截面的最大弯矩大于一致激励下的弯矩。2)当波速为300 m/s时，2号墩墩底最大弯矩是一致激励下的1.59倍；当波速为200 m/s时，3号墩墩底最大弯矩是一致激励下的1.32倍；当波速为400 m/s时，4号墩墩底最大弯矩是一致激励下的1.8倍。3)当波速为300 m/s时，1-1截面最大弯矩是一致激励下的1.25倍；当波速为300 m/s时，2-2截面最大弯矩是一致激励下的2.43倍；当波速为200 m/s时，3-3截面最大弯矩是一致激励下的2.01倍；当波速为400 m/s时，4-4截面最大弯矩是一致激励下的2.49倍。4)因此进行地震反应分析时从内力角度来看仅考虑一致激励，结构是偏于不安全状态的。

4.3 地震波双向正交分量联合作用

选取Fernando波沿顺桥向和横桥向两个方向进行输入。

4.3.1 不同波速下位移对比分析

根据理论计算模型，提取1号～5号墩墩顶纵向位移及主要控制截面1-1截面～4-4截面纵向位移见表6～表9。

表6 不同波速下各墩顶纵向位移(二)

表7 不同波速下各墩顶横向位移

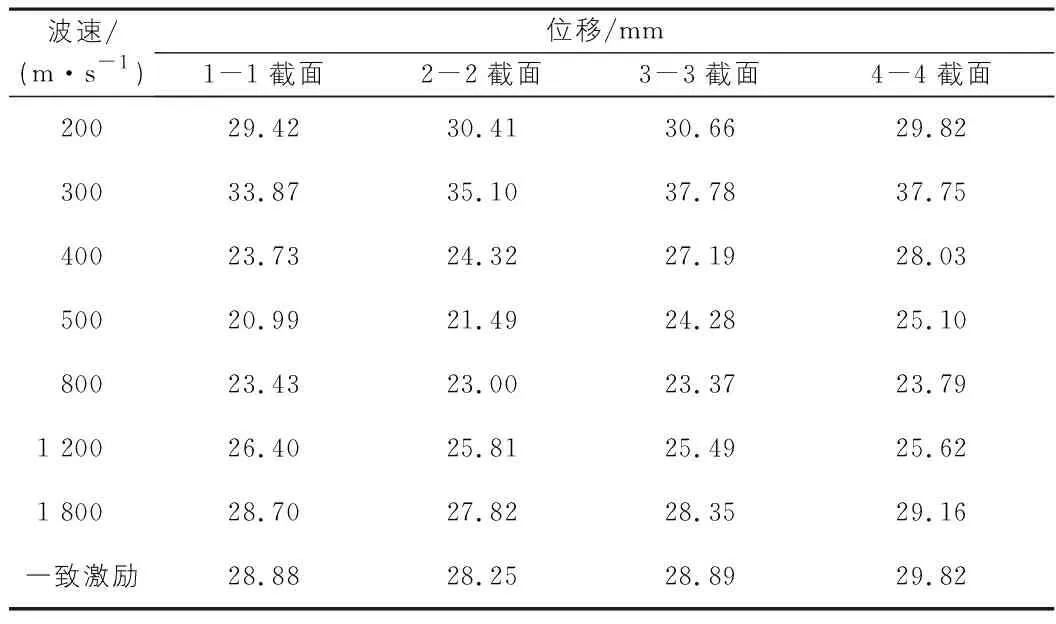
表8 不同波速下主要控制截面纵向位移(二)

表9 不同波速下主要控制截面横向位移

由表6，表9可知：1)地震波双向正交分量联合作用下墩顶及控制截面纵向位移同地震波纵向作用。2)当波速为1 800 m/s时，2号墩墩顶横向位移是一致激励的1.02倍；当波速为400 m/s时，3号墩墩顶横向位移是一致激励的1.30倍；当波速为800 m/s时，4号墩及5号墩墩顶横向位移分别是一致激励的1.29倍和1.22倍。3)当波速为1 800 m/s时，2-2截面横向位移是一致激励的1.04倍；当波速为800 m/s时，4-4截面横向位移是一致激励的1.29倍。4)因此进行地震反应分析时，从位移角度来看仅考虑一致激励，结构是偏于不安全状态的。

4.3.2 不同波速下内力对比分析

根据理论计算模型，提取1号～5号墩墩顶弯矩及主要控制截面1-1截面～4-4截面弯矩作为重点考察的量值，见表10～表13。

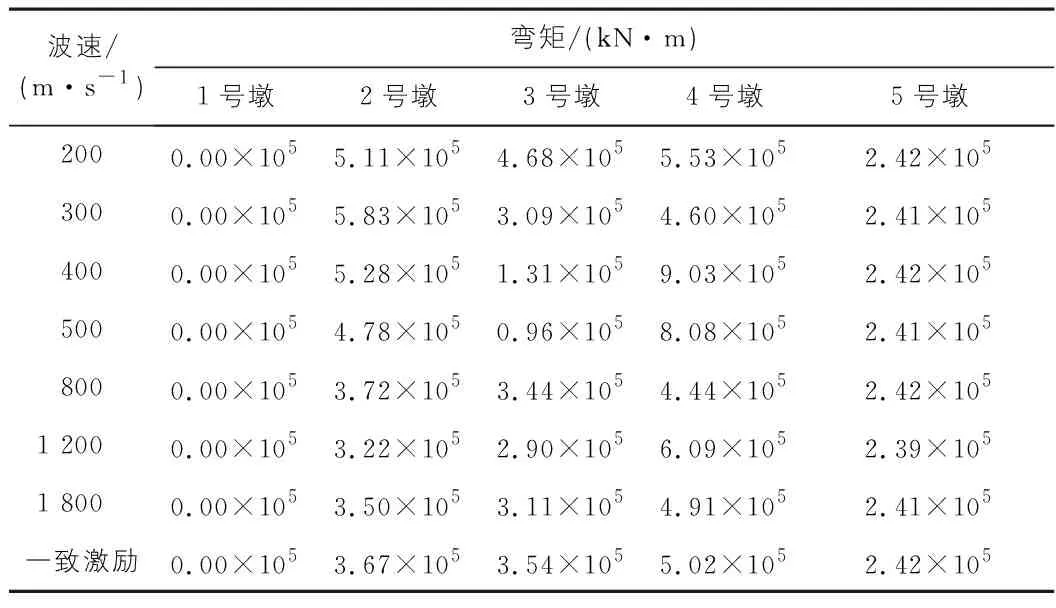
表10 不同波速下墩底弯矩My(二)

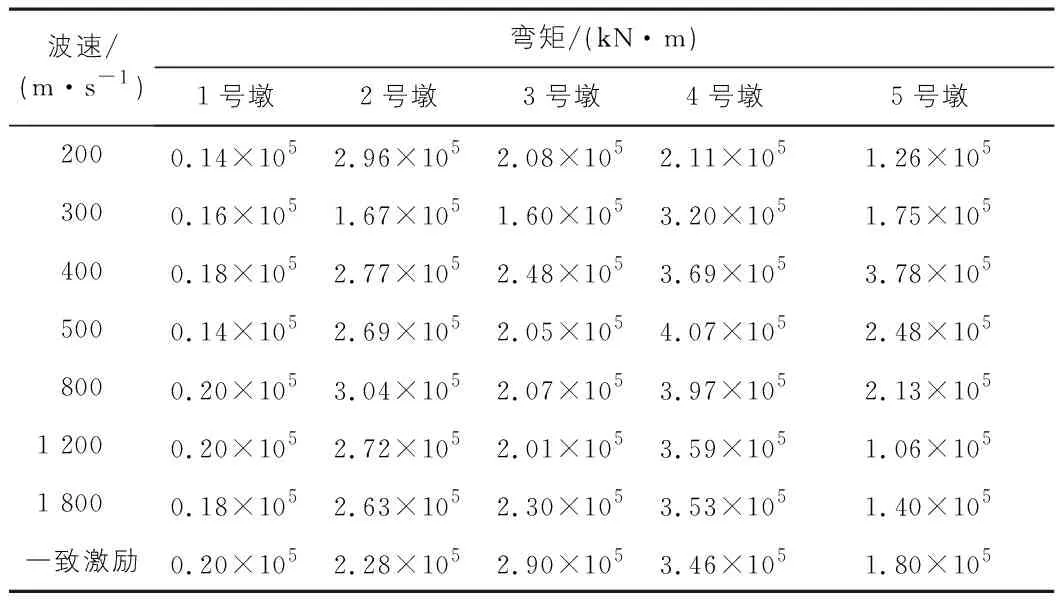
表11 不同波速下墩底弯矩My(三)

表12 不同波速下主要控制截面弯矩Mz(一)

表13 不同波速下主要控制截面弯矩Mz(二)

由表10，表13可知：1)地震波双向正交分量联合作用下墩底及控制截面My方向弯矩同地震波纵向作用。2)当波速为800 m/s时，2号墩墩底最大弯矩是一致激励下的1.33倍；当波速为500 m/s时，4号墩墩底最大弯矩是一致激励下的1.18倍；当波速为400 m/s时，4号墩墩底最大弯矩是一致激励下的2.1倍。3)当波速为1 800 m/s时，1-1截面Mz方向弯矩是一致激励的1.17倍；当波速为800 m/s时，2-2截面及3-3截面Mz方向弯矩分别是一致激励下的1.11倍和1.27倍；当波速为400 m/s时，4-4截面Mz方向弯矩是一致激励的1.42倍。4)因此进行地震反应分析时从内力角度来看仅考虑一致激励，结构是偏于不安全状态的。

5 结论

通过对加劲钢桁连续刚构桥进行行波效应分析得出以下结论：1)对大跨度加劲钢桁连续刚构桥进行抗震设计时，按一致激励进行地震响应分析并非总是偏于安全的。2)考虑行波效应时，结构的内力与位移和地震动的输入及自身特性有关，没有过多规律可言，但总体而言，视波速越小时结构的地震响应越大。3)在进行抗震研究时，应该根据场地条件选择不同地震波，分析不同视波速下的结构地震响应，并对比一致激励，选择最不利的情况进行抗震验算。