液固分选流化床内颗粒动力学方程的简化及应用

孙铭阳，韦鲁滨，朱学帅，李大虎，李阳，刘俊丽

(中国矿业大学(北京)化学与环境工程学院，北京，100083)

液固分选流化床(liquid-solid fluidized bed separator, LSFBS)是一种广义的散式流化床，既有粗重颗粒透过床层的向下运动，也有轻细颗粒由上升水流经溢流堰带出，分选过程中床层减少的颗粒则由入料流不断补充。从物料和流场角度讲，液固分选流化床内的流化和分选都是一种动态平衡过程，所说的液固分选流化床层即为主分选区内所有颗粒在上升水流和入料流作用下所形成的液固两相流动系统。全面考虑液固流化床层颗粒受力，精确研究颗粒−颗粒、颗粒−流体相互作用以得到准确的预测流场要付出很大的计算代价。实际上，研究颗粒在LSFBS内运动时，往往只对颗粒竖直方向的干扰沉降运动和最终分选结果感兴趣，可以合理忽略液固两相流动的一些细节，根据LSFBS主分选区的流场特点将不影响颗粒分离、分层结果的力忽略，而将不便于求解的力，如颗粒间相互作用，转化为便于求解的形式，进而将液固流化床层固相颗粒的流动简化。XIA等[1−2]对液固分选流化床颗粒受力分析进行了详细研究，而深入讨论各力量级以及密相流化床内颗粒间相互作用有效处理方法的研究较少。本文作者对液固分选流化床层内颗粒所受各力进行了量级比较，结合LSFBS主分选区内液固两相流动特点，确定各力取舍或将其转化为便于处理的形式；采用拉格朗日法，建立简化的颗粒动力学方程来描述LSFBS内颗粒运动。最后，用Runge-Kutta算法求解不同粒度、密度颗粒的动力学方程来得到颗粒速度和位移随时间的变化，并通过与试验数据对比来评价该简化的颗粒动力学方程建立过程的合理性以及方程本身的实用性。

1 LSFBS内颗粒受力分析及动力学方程的简化

可将 LSFBS内颗粒分离过程看作上升水流作用下沿竖直方向的沉降运动，从力与颗粒运动方向可将颗粒受力分为2类，即与颗粒运动平行或垂直的作用力。重力G、流体静压力、流体阻力FD、虚拟质量力FV和Basset力FB与颗粒运动方向平行，其中流体阻力、虚拟质量力和Basset力又称为颗粒所受广义阻力；Saffman力FS和Magnus力FM与颗粒运动方向垂直，称为广义升力。根据牛顿第二定律，颗粒竖直方向(z方向)运动的动力学方程为

式中：mp为颗粒质量；z为颗粒竖直方向位移；Ft为颗粒竖直方向所受各力的合力，包括流体施加的作用力、质量力以及颗粒−颗粒和颗粒−器壁之间的碰撞作用FC；uP为颗粒和流体速度的轴向分量。竖直方向的颗粒动力方程用拉格朗日法可表示为

式中：Fp为压力梯度力。

1.1 各力量级比较

颗粒所受重力与运动状态无关，量级与惯性力相同，自始至终都不能忽略；颗粒以一定速度进入LSFBS后即受到流体阻力作用，量级与质量力及惯性力相同，亦不能忽略。将主分选区内颗粒所受压力梯度力、虚拟质量力、Basset力、Saffman力和Magnus力量级与颗粒惯性力或流体阻力进行比较，并结合各力对颗粒竖直方向干扰沉降运动和分选结果的影响对各力进行简化或取舍。

1.1.1 压力梯度力

颗粒竖直方向所受压力梯度力可表示为

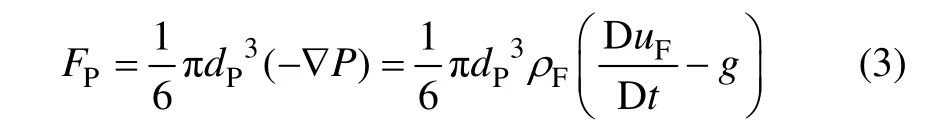
式中：dP为颗粒直径；ρF为流体密度；P为流物压力；g为重力加速度；μF为流体轴向速度分量；D/Dt为随体导数。

式(3)中由流场非定常引起，ρFg为流体静压力。LSFBS主分选区内流场可看做均匀稳定上升水流，因此，有：

即 LSFBS主分选区内压力梯度力可简化为流体静压力，量级与重力相同，不能忽略。

1.1.2 附加质量力

颗粒竖直方向所受附加质量力表达式为

式中：KV为附加质量力系数，是加速度模数AC的函数，其表达式[3]分别为

假设颗粒粒度和密度分别为 1 mm和 1 500 kg/m3，水的密度和黏度分别取 998 kg/m3和 1.003 mPa.s，|uP−uF|取 0.01 m/s。由计算可知：LSFBS 正常运行时，颗粒与流体相对加速度绝对值不超过重力加速度，取最大值为10 m/s2，得到单位质量颗粒所受附加质量力为0.33d(uP−uF)/dt，即附加质量力与颗粒惯性力量级相同；当ρF，dP以及颗粒与流体介质间相对速度uP−uF一定时，不难发现附加质量力系数KV是相对加速度绝对值的减函数，即随着相对加速度绝对值的减小，附加质量力与惯性力比值逐渐增大。以上分析表明，LSFBS正常运行时，颗粒所受附加质量力总是与惯性力有相同量级，因此不能忽略。

1.1.3 Magnus力和Saffman力

将 LSFBS内颗粒与流体微元速度分解为径向和轴向 2个分量。在上升水流作用下(轴向)，因颗粒旋转产生的 Magnus力在轴向上没有分量，对颗粒竖直方向的干扰沉降没有直接影响；径向水流作用区域主要位于入料口下方较小的范围内(其他分选区域内径向水流速度很小，可以忽略)，该区域内因颗粒旋转可产生轴向的Magnus力分量。

Saffman力方向与速度梯度方向平行，在LSFBS大部分分选区域内，流体速度梯度的轴向分量可以忽略，同样只有在入料口下方区域，流体速度梯度的轴向分量才相对显著[4−5]。

颗粒所受Magnus力如下式所示[6]

式中：ω为颗粒相对流体的旋转角速度；CLM为Magnus力系数，高颗粒雷诺数下(ReP＜140)的升力系数修正[7]为

式中：ReP为颗粒雷诺数；ReR为颗粒相对流体的旋转雷诺数，ReR=ρFdP.dP|ω|/μ；μ为黏度。

LSFBS内颗粒雷诺数主要位于过渡区[7]，假设颗粒自旋方向与液体速度方向垂直(升力最大)，令流体阻力系数CD=13/ReP0.5，则单位质量颗粒所受Magnus力与流体阻力之比为

假设颗粒性质与上文相同，则LSFBS内粗煤泥颗粒所受两力之比如表1所示。

由表1可以看出：过渡区内，随着颗粒直径和颗粒自旋角速度增大，Magnus力与流体阻力的比值逐渐增大；当颗粒直径大于3 mm且自旋角速度大于5 rad/s时，粗煤泥颗粒所受Magnus力量级与流体阻力相同；当颗粒直径为1 mm、自旋角速度为1 rad/s时，颗粒所受Magnus力量级与流体阻力的比值仅为0.033。实际分选中，LSFBS入料粒度范围一般为 0.25~1.00 mm，且LSFBS的液固流化床层为密相液固两相流，颗粒的自旋角速度较小[2]，因此，可以将该力省略。

表1 Magnus力与流体阻力量级比较Table 1 Magnitude comparison between Magnus and drag force

颗粒所受Saffman力如下式所示[8]：

式中：ωF为流体旋度；f(α)为颗粒雷诺数和流体旋度雷诺数Reω的函数，具体形式为[9]

假设颗粒与流体的相对速度为 0.01 m/s，则0.25~3.00 mm颗粒的特征雷诺数处于2.5~30.0之间，得单位质量颗粒所受Saffman力与流体阻力比值为

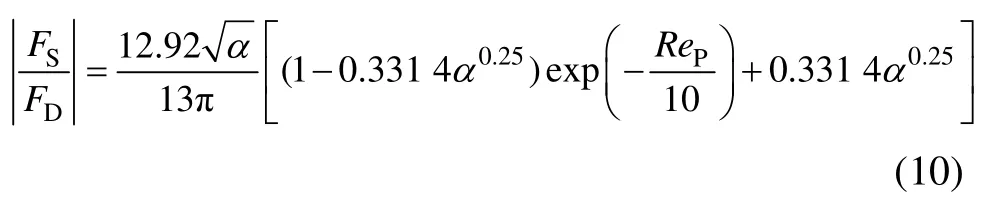
计算得LSFBS内单位质量颗粒所受Saffman力与流体阻力之比如表2所示。

表2 Saffman力与流体阻力量级比较Table 2 Magnitude comparison between Saffman and drag force

由表 2可以看出：当速度梯度大于 10 s−1时，Saffman力与流体阻力量级相同。虽然在入料流射流边界层内速度梯度的轴向分量相对显著，但是数值模拟结果显示也只有 10−1~100数量级[5]，且该区域的径向和轴向范围与整个分选区相比非常小，固亦可将Saffman力忽略。

1.1.4 Basset力

颗粒所受Basset力如下：

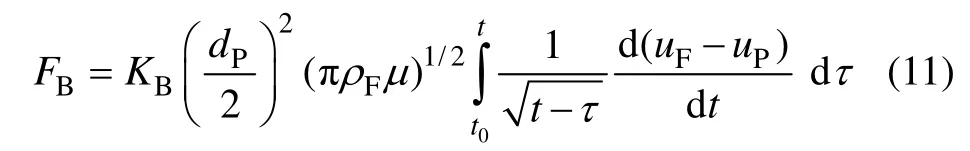
式中：KB为Basset力系数[3]；τ为时间。

为了精确的求解流场中颗粒运动轨迹，Basset力的求解方法以及对颗粒运动的影响受到了越来越多的关注[10−15]。采取文献[15]中的方法，将颗粒与流体的相对加速度用差分的形式表示为常数，单位质量颗粒所受Basset力与流体阻力之比可表示为

令 Δt=t−t0，由式(12)可见，过渡区内，Basset力与流体阻力比值是颗粒粒度和Δt的函数。令分选过程中某时刻颗粒与流体相对速度为0.01 m/s，不同Δt、不同粒度颗粒所受Basset力与流体阻力比值见表3。

由表3可以看出：随着颗粒直径增大或Δt减小，Basset力与流体阻力之比越来越大，且 Δt对 Basset力的影响要更加显著；当Δt小于1 s时，Basset力超过流体阻力。需要注意的是，式(11)是稀疏两相流中颗粒所受Basset力公式，该式对于颗粒间相互作用不能忽略的密相两相流动的适应性还需要进一步研究[16]。此外，刘小兵等[12]认为：在定常流场中运动时，可以忽略Basset力的影响；VOJIR等[17]利用微积分变换的方法[18]对不同条件下Basset力对颗粒运动的影响进行了数值研究，发现当数值计算只对时间积分效果感兴趣时，在随机流动速度场中颗粒所受到的 Basset力可以忽略。与某时刻颗粒的加速度相比，更重要的是某颗粒进入其主分选区流场后的归属问题，即一定分选时间内，颗粒加速度在该分选时间内的积分。鉴于液固分选流化床主分选区流场可看作定常流以及Basset力对求解某时刻颗粒的干扰沉降速度和位移影响不大，况且密相流固系统中还没有合适的Basset力表达式，因此，将Basset力从颗粒动力学方程中省略。

表3 Basset力与流体阻力量级比较Table 3 Magnitude comparison between Basset and drag force

1.2 颗粒间相互作用的近似处理

悬浮液中颗粒间相互作用体现在2个方面。首先，颗粒之间存在直接碰撞作用；其次，周围颗粒的存在改变了颗粒周围流体的流动状态，从而间接影响了颗粒的运动。

可将液固流化床层类比为准流体，以该准流体有效密度和表观黏度来体现周围颗粒对目标颗粒运动的影响。假设液固流化床层内共有m个密度级，每个密度级又分为n个粒度级，对于均匀稳定的液固流化床，颗粒表面某点处所受压力与床层高度的关系可表示为

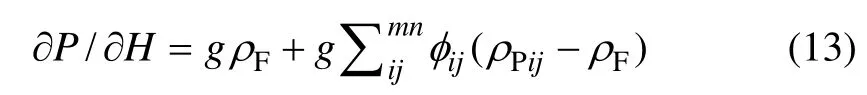
令ρeff为液固流化床层有效密度，由式(13)得：

式中：φij为i密度级、j粒度级颗粒在床层所占体积分数；为i密度级、j粒径级颗粒的平均密度。

床层有效动力黏度(或者称为流变黏度，即剪切应力与此时应变速率之比)，可按 Swanson的半经验公式[19]计算：

式中：φmax为所有组分颗粒均匀混合时所能达到的固相最大体积分数；φ为实际液固流化床层内所有颗粒组分的体积分数之和；μ0为颗粒体积分数为0时的床层动力黏度。

Swanson公式的优点在于引进了颗粒最大堆积体积分数，有效避免了悬浮液中颗粒体积分数接近最大堆积体积分数时计算误差偏大的问题。这种优势在计算颗粒干扰沉降速度时表现更为明显。

2 颗粒动力学方程的应用

2.1 颗粒动力学方程的求解

将式(2)中广义升力、Basset力舍去，并将其余各力中水的密度和黏度分别用床层有效密度和表观黏度来代替以体现周围颗粒对目标颗粒运动的影响，最终得到液固分选流化床内简化的颗粒动力学方程为

实际生产中大部分轻细颗粒在入料口附近即完成分选，如果计算主分选区床层平均密度时包括了入料中所有颗粒，所得计算结果将高于实际情况；此外，实际床层密度是非均匀的，沿轴向有一定梯度。在用式(16)预测颗粒在LSFBS内分离过程时，可根据实验结果将流体阻力乘以一经验系数，以对上述2个问题进行修正。

令液固分选流化床层内均匀稳定上升水流速度为uF=C。由于附加质量力系数含有 d(uP−uF)/dt，因此，式(16)所示的颗粒动力学方程为隐式，计算之前应将其转化为显式。颗粒与流体相对速度的加速度可表示为

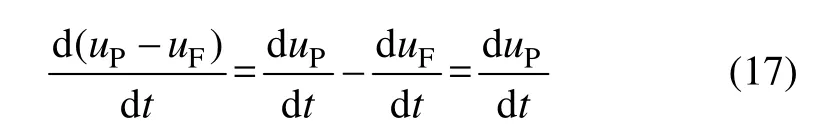
细粒矿物分选过程中，颗粒雷诺数一般小于1 000，从准确度高和形式简单2方面考虑，式(16)中阻力系数选择 Schiller–Naumann模型，CD=24(1+0.15ReP0.687)/ReP。将AC，CD，uF以及式(17)代入式(16)，可得

可利用MATLAB求解式(18)，为书写方便，将求解结果表示为

颗粒进入液固流化床层后，某时刻所处的位置通过求解下式得到：

常微分方程的求解方法主要有欧拉法、Runge-Kutta法和预估−校正法。其中，四阶Runge-Kutta法的局部截断误差为O(h5)，被广泛应用于求解微分方程的初值问题，本文采用经典的四阶Runge-Kutta法来同时求解式(19)和式(20)。

2.2 动力学方程的验证和应用

首先利用简化的颗粒动力学方程来预测不同体积分数时单一组分颗粒在水中的干扰沉降运动，以验证式(16)的准确性。

搭建了颗粒流化试验系统如图1所示。上升水流由平行管流体分布器射出后，在液固流化床柱体内向上流动并沿径向逐渐均匀分布，经第 1层孔径 0.045 mm筛网后，流体径向速度基本实现均匀。待流化颗粒放置于第2层筛网上，第2层筛网孔径也为0.045 mm，以得到均匀稳定的液固流化床层，同时筛孔远小于待流化颗粒粒径，保证底层颗粒受到较均匀向上的流体曳力，且不会沿近壁面区漏下。

图1 液固流化试验系统Fig. 1 Experiment system for Liquid-Solid Fluidization

准备一定质量的粒度分别为 0.25~0.35 mm和0.63~0.75 mm煤粒以及粒度分别为0.25~0.35 mm和0.50~0.63 mm石英砂颗粒作为流化颗粒。4种流化颗粒相关性质及4种颗粒构成的初始床层性质如表4所示，其中H0为粒群在完全流化时突然让上升水流速度为0 m/s，待颗粒在水中自由沉降完成后，在第2层筛网上形成的固体颗粒床层的初始高度，φ0则为此时固体颗粒床层对应的固体体积分数。通过比重瓶测出各组颗粒的真实密度。利用比重杯测出一定体积V下颗粒达到最密堆积时的质量MP，根据式(21)计算出各组颗粒最大堆积体积分数：

表4 流化颗粒性质Table 4 Properties of fluidized particles

稳定流化床层形成后，某一时刻，床层内所有颗粒相对壁面的平均速度为0 m/s，因此，对于整个床层来讲，此时床层内部所有颗粒整体上达到了相应颗粒体积分数下的干扰沉降末速，根据颗粒体积分数与流化速度得到此时颗粒干扰沉降末速uslip为

令H为上升水流速度为uF时颗粒床层高度，则此时液固流化床层内颗粒平均体积分数为

对0.25~0.35 mm和0.50~0.63 mm石英砂颗粒以及0.25~0.35 mm和0.63~0.75 mm煤粒不同体积分数时的干扰沉降末速进行预测，将得到的预测值与试验值进行对比，如图2所示。

由图2可以看出：本文提出的简化的颗粒动力学方程能相对精确的预测各种颗粒干扰沉降末速，其相对误差基本可控制在5%以内。

基于 LSFBS流场和颗粒分离过程特点对颗粒动力学方程进行简化，其最终目的在于利用简化的颗粒动力学方程来预测入选物料(多组分颗粒)在LSFBS内的分选结果。按照文献[20−21]中的入料性质及LSFBS结构参数，用式(16)分别预测了相应条件下入料颗粒在LSFBS内的干扰沉降运动，得到不同密度颗粒在底流中分配率的预测值与试验值的差异如图3所示。

由图3可以看出：各密度级分配率的预测值都能较好地与试验值吻合，其中，所有密度级颗粒在底流中分配率的预测值与文献[20−21]中试验值间的均方根误差分别为5.05和3.33，溢流产率的相对误差分别为2.84%和3.82%，说明式(16)能较正确地预测不同密度颗粒在LSFBS内的分选结果。

图2 颗粒干扰沉降末速预测值与试验值对比Fig. 2 Comparison between predicted and experimental hindered settling velocities at different particles volume fractions

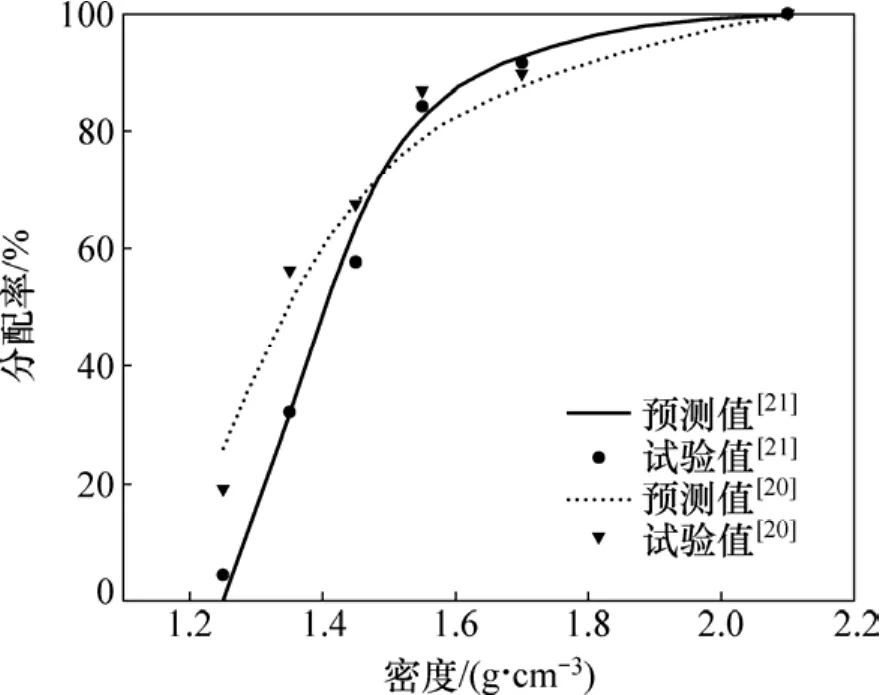
图3 颗粒分选结果预测值和试验值对比Fig. 3 Separation results comparison between predicted and experimental values

3 结论

1)从各力量级比较结果发现LSFBS主分选区内颗粒所受压力梯度力、附加质量力与惯性力量级相同；当颗粒直径大于3 mm且自旋角速度大于5 rad/s或当地速度梯度大于10 s−1时都能使广义升力达到流体阻力量级；Basset力与流体阻力之比是颗粒直径和Δt函数，当Δt小于1 s时， Basset力可达到流体阻力量级。

2)Magnus力、Saffman力和Basset力对颗粒在竖直方向的干扰沉降运动影响很小，可将其从颗粒动力学方程中省略；而粒群干扰沉降运动对目标颗粒周围流场的影响以及与目标颗粒的直接碰撞作用可通过液固悬浮液有效密度和有效黏度的概念来体现，其中引入颗粒最大堆积率并选择Swanson的半经验公式来计算液固悬浮液有效黏度。

3)简化的颗粒动力学方程所预测的不同体积浓度下各种颗粒干扰沉降末速相对误差基本可控制在5%以内；与2组分选试验结果相比，所预测的各密度颗粒分配率的均方根误差分别为5.05和3.33，溢流产率相对误差分别为 2.84%和 3.82%，表明该简化的颗粒动力学方程能较准确地预测颗粒在 LSFBS干扰沉降运动和分选结果，也说明根据LSFBS主分选区颗粒分离过程和流场特点对颗粒动力学方程进行简化的思路是合理的。

[1]XIA Y. Numerical simulation of fine particle separation in hindered-settling bed separators by computational fluid dynamics[D]. Morgantown: West Virginia University. College of Engineering and Mineral Resources, 2004: 15−25.

[2]李延锋. 液固流化床粗煤泥分选机理与应用研究[D]. 徐州:中国矿业大学化学与环境工程学院, 2008: 63−65.LI Yanfeng. Study on the separation mechanism and application of liquid-solid fluidized bed coarse slime separator[D]. Xuzhou:China University of Mining and Technology. College of Chemical and Environmental Engineering, 2008: 63−65.

[3]ODAR F. Verification of the proposed equation for calculation of the forces on a sphere accelerating in a viscous fluid[J]. Journal of Fluid Mechanics, 1966, 25(3): 591−592.

[4]韦鲁滨, 孙铭阳, 孟丽诚, 等. 基于 CFD 的液固分选流化床数值模拟[J]. 煤炭学报, 2016(7): 1820−1826.WEI Lubin, SUN Mingyang, MENG Licheng, et al. Numerical studies of liquid-solid fluidized bed separator using CFD[J].Journal of China Coal Society, 2016, 41(7): 1820−1826.

[5]孙铭阳, 韦鲁滨, 朱学帅, 等. 液固分选流化床三相流场模拟中各粘性流动模型的适用性[J]. 过程工程学报, 2016, 16(1):86−93.SUN Mingyang, WEI Lubin, ZHU Xueshuai, et al. Research on performances of different viscous models in simulation of flow field in liquid-solid fluidized bed separator[J]. The Chinese Journal of Process Engineering, 2016, 16(1): 86−93.

[6]SI R, JB K. The transverse force on a spinning sphere moving in a viscous fluid[J]. Journal of Fluid Mechanics, 1961, 11(3):447−459.

[7]孙铭阳, 朱学帅, 韦鲁滨. 细粉煤粒度分布特性的研究[J]. 太原理工大学学报, 2016, 47(4): 436−444.SUN Mingyang, ZHU Xueshuai, WEI Lubin. Studies of size distribution characteristics of fine coal[J]. Journal of Taiyuan University of Technology, 2016, 47(4): 436−444.

[8]SAFFMAN P G. The Lift on a Sphere in a Slow Shear Flow[J].Journal of Fluid Mechanics, 1965, 22(2): 385−400.

[9]MEI R. An approximate expression for the shear lift force on a spherical particle at finite reynolds number[J]. International Journal of Multiphase Flow, 1992, 18(1): 145−147.

[10]LI L, MICHAELIDES E E. The magnitude of basset forces in unsteady multiphase flow computations[J]. Journal of Fluids Engineering, 1992, 114(3): 417−419.

[11]黄社华, 程良骏. 非定常流场中颗粒运动所受 Basset力的性质解析[J]. 力学与实践, 1996(3): 50−54.HUANG Shehua, CHENG Liangjun. A study of Basset force for particles moving in the unsteady flow[J]. Mechanics in Engineering, 1996(3): 50−54.

[12]刘小兵, 程良骏. Basset力对颗粒运动的影响[J]. 四川工业学院学报, 1996(2): 55−63.LIU Xiaobing, CHENG Liangjun. Influence of Basset force on the movement of particles[J]. Journal of Sichuan Institute of Technology, 1996(2): 55−63.

[13]DORGAN A J, LOTH E. Efficient calculation of the history force at finite Reynolds numbers[J]. International Journal of Multiphase Flow, 2007, 33(8): 833−848.

[14]BOMBARDELLI F N A, GONZÁLEZ A E, NIÑO Y I.Computation of the particle basset force with a fractional-derivative approach[J]. Journal of Hydraulic Engineering, 2008, 134(10): 1513−1520.

[15]黄社华, 李炜, 程良骏. 任意流场中稀疏颗粒运动方程及其性质[J]. 应用数学和力学, 2000, 21(3): 265−276.HUANG Shehua, LI Wei, CHENG Liangjun. On equation of discrete solid particles’ motion in arbitrary flow field and its properties[J]. Applied Mathematics and Mechanics, 2000, 21(3):265−276.

[16]由长福, 祁海鹰, 徐旭常. Basset力研究进展与应用分析[J].应用力学学报, 2002, 19(2): 31−33.YOU Changfu, QI Haiying, XU Xuchang. Progresses and applications of basset force[J]. Chinese Journal of Applied Mechanics, 2002, 19(2): 31−33.[17]VOJIR D J, MICHAELIDES E E. Effect of the history term on the motion of rigid spheres in a viscous fluid[J]. International Journal of Multiphase Flow, 1994, 20(3): 547−556.

[18]MICHAELIDES E E. A novel way of computing the Basset term in unsteady multiphase flow computations[J]. Physics of Fluids A Fluid Dynamics, 1992, 4(7): 1579−1582.

[19]KOHMUENCH J N. Improving effciencies in water-based separators using mathematical analysis tools[D]. Blackburg:Virginia Tech. Department of Mining and Minerals Engineering,2000: 49−51.

[20]LÜ Yibo, ZHU Yuanxin. Evaluation of numerical simulation for the separation of fluidized bed coarse slime[J]. Energy Procedia,2012, 17: 954−960.

[21]SHA Jie, XIE Guangyuan, WANG Hong, et al. Effect of the column height on the performance of liquid-solid fluidized bed for the separation of coarse slime[J]. International Journal of Mining Science and Technology, 2012, 22(4): 585−588.