基于改进联合采购及配送模型的RFID投资决策研究

崔利刚，邓 洁，王 林，张金隆，许茂增

(1. 重庆交通大学经济与管理学院,重庆 400074；2. 华中科技大学管理学院，湖北 武汉 430074；3. 重庆理工大学知识产权学院,重庆 400054)

1 引言

联合采购问题(Joint Replenishment Problem, JRP)是指从一个供应商处对多品进行分组采购，从而分摊主要准备费用，减少订货频次，其学术价值和适用性被广泛认同[1-6]。随着研究的深入，不少学者对经典JRP在采购端进行了扩展，比如通过放松确定性需求的假设研究随机JRP[4]，或通过增加资源或运输条件约束(Wang Lin等[2])构建(资源)约束型JRP。尽管目前对配送调度问题的研究较多并取得良好的效果[7-9]，遗憾的是目前文献较少考虑多品联合采购和配送相结合的优化问题。其实，联合采购与配送(Joint Replenishment and Delivery, JRD)协同优化可以整合运输资源并可获得批量折扣，此策略已被跨国流通企业广泛采用。跨国零售巨头沃尔玛为推动供应商多品种、小批量、多批次商品补货，在旗下500家连锁店安装RFID设备追踪商品信息，实现多种商品按需补货和商品及时配送上架，以维持其“天天低价”战略。在国内，零售商家乐福在位于天津武清开发区的华北物流中心整合华北地区超市的采购需求，向上游供应商联合补货，并向下游区内连锁超市进行统一配送，籍此提高其与供应商的议价能力和超市网点的响应能力，实现采购和配送成本的双降。

目前，JRD已经被Cetinkaya等[10]、Sindhuchao等[11]、Cha等[12]、Qu Hui等[13]、Wang Lin等[14]和Moon和Cha[15]进行过研究。但是在他们的研究中，配送假设或太弱使问题过于复杂且难于处理，如Sindhuchao等[11]；或假设太强，将配送过程预设为一对一的配送过程，或只考虑配送的频率问题，丧失了问题的一般性和实际的参考价值，如Cha等[12]和Moon和Cha[15]。因此，针对JRD问题下的一对一的配送问题，需要进一步优化针对多个客户、不同商品的车辆巡回配送问题，对集中配送商品的运输路径进行优化，这也是本研究区别于现有研究的一个主要差别。

近年来，无线射频识别(Radio Frequency Identification, RFID)技术作为物联网的关键技术，以其便捷、高效的巨量数据采集处理能力，在物流与供应链管理领域被广泛应用，RFID研究逐渐成为学术界研究的热点[16-17]。目前的研究显示投资RFID主要用于解决库存不确定性问题、牛鞭效应问题和采购策略问题[18]。当前RFID投资评估或集中于对整个供应链的长期关注，如Bottani 和Rizzi[19]对基于RFID的快速移动商品的5年调查；或集中于供应链具体环节，如考虑RFID的货架定价问题[20]。范体军等[21, 22]建立RFID成本和效率之间的线性关系和张李浩等[23-24]探讨了基于RFID投资的供应链协调问题，这些工作为后续的研究奠定了良好的基础。

投资策略与投资收益的研究一直以来都是学术研究的热点问题[25-27]。然而，针对具有重要理论价值和较高实用价值的JRD复杂系统决策问题，非常缺乏相关文献研究RFID投资对JRD的影响。为此，本文参考Lee和Lee[28]采用的规范性方法，考虑引入RFID后对订货、库存、运输等过程的影响，寻求合理的RFID投资规模。本文假定RFID对整个JRD过程的订货效率和JIT效率产生影响，其中对订货效率的影响包括采购过程订货成本的影响和配送过程中运输成本的影响；对JIT效率的影响主要包括库存成本的影响和顾客等待成本的影响。

另外，JRD已被证明是NP难题，模型求解非常复杂[12]。而传统的方法又存在自身难以克服缺陷：(1)枚举法在枚举空间比较大时，算法效率较低，经常在规定时间无法得到可行解。(2)常规的启发式算法对每个问题必须找出特有的启发式规则，难度高且无通用性。(3)也有学者采用遗传算法(Genetic algorithm, GA)进行求解[12]，结果证实GA也是一种可行的方法，但GA存在复杂的进化操作使其计算费用随着问题规模的扩大和复杂度的提高呈指数级增长，且算法搜索后期容易出现停滞现象。作为一种随机的并行直接搜索算法，差分进化(Differential Evolution, DE)算法保留了基于种群的全局搜索策略，具有算法通用、容易实现、协同搜索、易于与其他算法混合等优点。DE算法以其易用性、稳健性和强大的全局寻优能力在众多包括在联合采购相关领域取得成功[13]。因此，采用DE算法来解决基于RFID的JRD投资决策模型求解难题，也是可行的。

因此，本研究的目的在于构建一种基于RFID的联合采购与配送调度投资决策新模型，该模型科学实用；同时，设计一个简单高效的DE智能求解算法；进而对JRD相关参数和RFID投资决策相关参数进行了敏感性分析，以得到有益的管理启示。

2 模型构建

JRD问题的研究背景是：首先，网络用户对多品发出需求订单；其次，中心仓库通过全球采购的形式补充商品，并以仓库为中心对网络用户进行定期配送；最后，仓库根据采购商品的数量和到达时间对商品的配送周期做出决策，同时考虑用户的具体位置，决定客户的访问顺序，使总成本最低。在这个过程中，中心仓库需要同时对不同商品的采购频率、联合采购周期和配送周期及最长配送路径进行优化。

模型用到的参数如表1：

表1 模型参数及说明

2.1 基本JRD模型

JRD基本模型的重要假设包括：(1)在整个计划周期内，商品i在两个连续的配送(从中心仓库到顾客)间隔内，保持恒定；(2)商品组合配送的配送量保持恒定。JRD模型分为两个过程，即采购过程和配送过程，如图1所示。

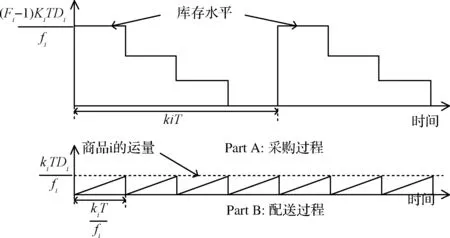
图1 基本JRD采配过程

JRD单位时间总成本TC的表达式，如式(1)所示：

(1)

其中，TC由四项成本加总构成。具体来看，(1)式右侧第一项订货成本CO、第二项库存成本CH、第三项对外运输成本CT和最好一项顾客等待成本CW；而T，K，F即所求的决策变量。其启发式求解的一般原理是：对于给定的K和F，总成本函数关于T是凸的，通过不断转换K和F组合更新T，使总成本最低。因此，每阶段对TC关于T求导可得：

(2)

而对于fi和ki的求解，通常采用固定一个值，求取另一个值的做法。即根据式(2)确定T和给定初值fi之后，再根据两个条件TC(ki)≤TC(ki-1)和TC(ki)≤TC(ki+1)，结合式(1)确定ki为：

(3)

在确定T和ki之后，可以返回来求fi。fi与ki的求解类似，fi求解仍需要满足两个条件TC(fi)≤TC(fi+1)和TC(fi)≤TC(fi-1)，并结合式(1)，确定ki为：

(4)

JRD基本模型存在着以下不足：仅在概念上解决特定采购和简单配送问题，要求需求和配送时间的稳定性；没有考虑协同配送问题，配送过程假设运输是一对一的。本文针对现有研究中配送过程的不足进行改进，同时考虑RFID对JRD系统的影响，建立基于RFID的JRD新模型。

2.2 基于联采联配协同的改进JRD模型 (JRD1)

在实际配送中，假设这些顾客是通过网络发出需求订单，被联合采购的商品会被配送给多个顾客。显然，如果所有的联合采购商品均采用一对一配送的话，配送成本会很高，所以传统配送策略具有很大的提升空间。本文将改进配送策略的JRD称为JRD1，下文用到的模型参数如表2：

表2 JRD1模型参数及说明

其中，p=1,2,…,P。如果p=0，表示中心仓库；否则p表示顾客。对于dp1p2，我们有p1≠p2，并且p1,p2=0,1,2,…,P。

假设商品i对外运输的频率的决定系数为αi，且αi=ki/fi。通过图1可知，对外配送的间隔由ki、fi共同决定的，配送间隔期即αiT，且αiT=(ki/fi)·T。从而我们可以判断，具有相同αi的商品可以考虑集中配送，而具有不同αi的商品分开配送，决策过程如下：

(1)如果一个或者多个αi(i=1,2,…,n)各不相同，对应的配送采用原一对一策略；

(2)如果存在多个αi(i=1,2,…,n)相同，对应的商品被放在一起进行组合运输。

这里有两种类型的匹配需要考虑：订单与顾客匹配，顾客的数量与顾客位置进行匹配，共需四步：

(1)确定被单独运输的订单和被组合配送的订单：如果订单被单独运输，根据公式(1)第三项计算配送成本，否则，转步骤(2)；

(2)这里定义一个二值变量xp,i，且xp,i={0,1}，xp,i=1，当且仅当商品i被顾客p购买，否则xp,i=0。所以订单和顾客匹配结果是一个P×n矩阵，我们定义为A，且xi,p∈A，转步骤(3)；

(3)确定服务向量。令A右乘M，并令结果向量Serv=A×M，转步骤(4)；

(4)确定订单的发出顾客。如果Serv的元素不等于0，其对应的顾客发出订单，并且元素的大小代表商品的类型，如果Serv的元素等于0，对应的顾客未发出订单。

路径优化问题已经存在很多的程序，这里仅采用一个简单的系数排序的算法。具体过程如下：

(1)随机产生P个在区间(0,1)内的数，并将这P个数与供应商数量对应；

(2)确定排序：按照从小到大的顺序对P个数进行排序；

(3)根据系数排序结果确定顾客的访问顺序。

一个6个顾客的实例用以表示顾客的访问过程被显示在图2中。在顾客访问顺序被确定以后，6个顾客的访问顺序是0-5-1-4-3-2-6-0 (其中0表示中心仓库，自然数代表顾客)。

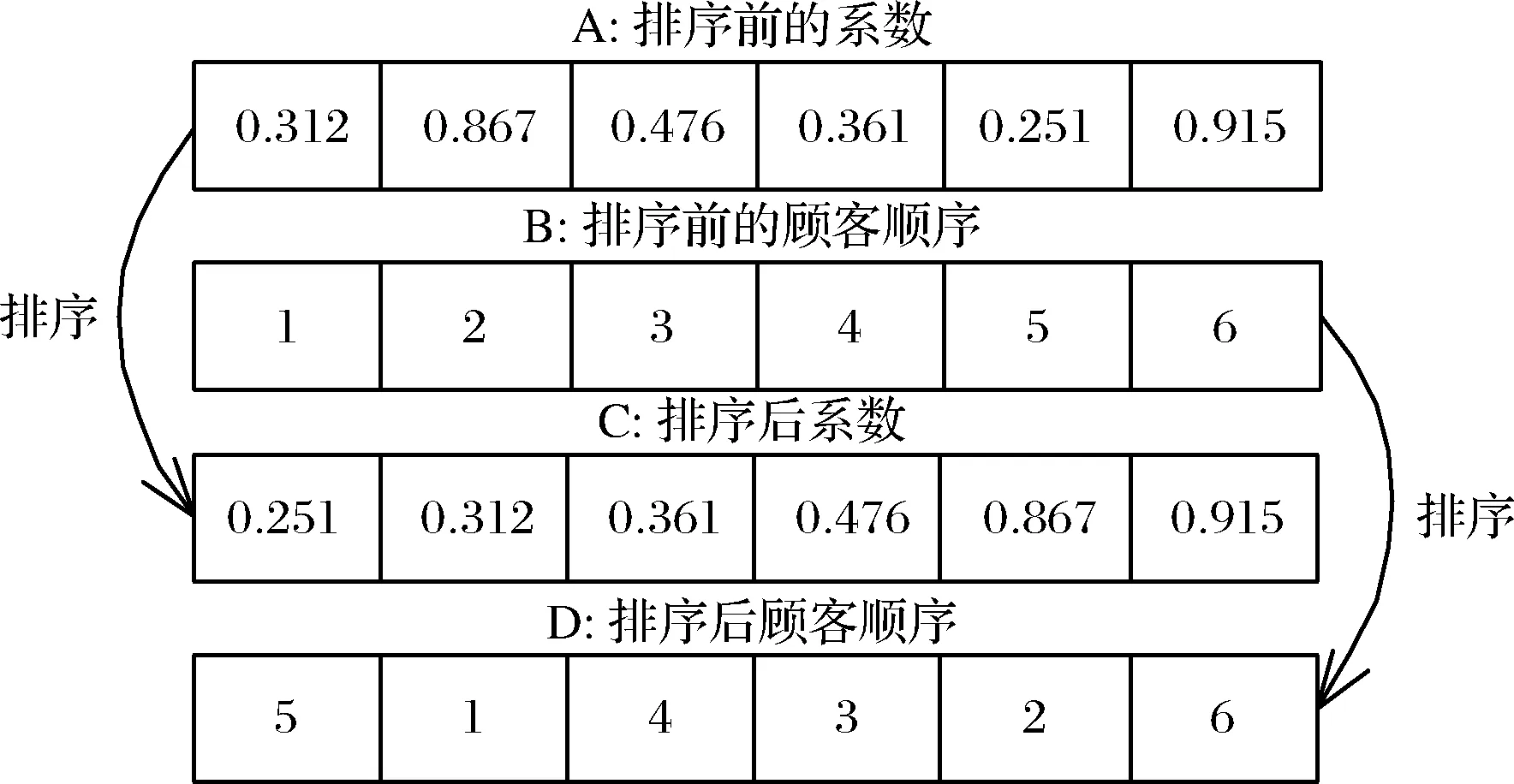
图2 顾客访问排序

分析图2可知，单商品的运输成本可根据运输的距离计算，借鉴车辆路径模型，可得运输成本如下：

(5)

(6)

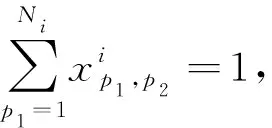
(7)

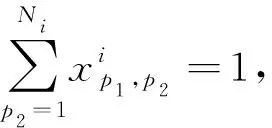
(8)

∑p1,p2∈S×Sxp1,p2≤|S|-1,S⊂{1,2,…,Ni},S≠Φ

(9)

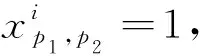
2.3 基于改进JRD的RFID投资模型 (JRD2)

为了便于区分，把RFID投资下的JRD问题称为JRD2，该模型相关参数如表3：

表3 JRD2模型参数及说明

由于本文假设RFID投资对订货效率的影响体现在其对订货成本和运输成本产生的影响，RFID投资对JIT效率的影响体现在其对库存成本和顾客等待成本产生影响。因此，根据式(1)，JRD2模型的总成本TC2：

(10)

其中，TC2由六项成本构成。具体来看，公式(10)右侧项依次为基于效率提升下的订货成本、库存成本、配送成本和顾客等待成本，最后两项分别为RFID订货效率提升投资成本和配送效率提升投资成本。

通过式(10)可知，如果I=1，则意味着对JRD过程无JIT效率提升；如果I=0，则意味着商品订单发出即被完成，无库存成本及顾客的等待成本发生，实现客户服务的“Just in Time”。同样，如果R=1，则意味着对RFID对JRD过程无订货效率和配送效率的提升；当R=0意味着供应能力的无限大。而且，为了找到最佳的I和R的关系，I和CI的关系，以及R和CR的关系，我们需要建立一个联系这些相互关系的函数表达式。这里我们仍采用Lee和Lee[28]提出的RFID投资效率是投资成本的以e为底数的指数函数，所以采购效率函数和JIT效率函数分别被表示为：

I=V+(U-V)e-λCI

(11)

R=N+(M-N)e-βCR

(12)

其中，0≤V≤U≤1，U是最低的JIT效率，即无RFID投资时的效率，V是RFID实施后的最高效率；0≤N≤M≤1，M是订货的最低效率，即无RFID投资时的效率，N是RFID实施后的最高效率。这里U,V,M,N的值可以根据RFID实施的成功经验，通过调研相关行业RFID的使用对效率的影响可以估算出来。λ和β为RFID投资影响的控制系数，用于控制RFID投资效果。

为了分析RFID投资所产生的效率提升情况，将式(11)和(12)带入式(10)中，如果TC2(T,K,F,I,R)对I求导并令其为零，可得以下方程：

(13)

通过式(11)可知，如果我们能够确定CH和CW得到最优的I*：

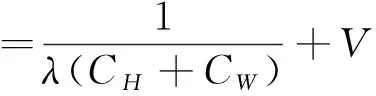
(14)

同理，针对式(10)，令TC2(T,K,F,I,R)对R求导并令其为零，并且如果能够确定CO和CT，也能够得到最优的R*：

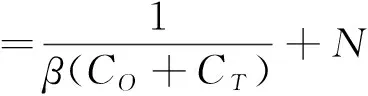
(15)

3 模型求解

Cha等[12]已证明JRD为NP-Hard问题，因此本文采用DE算法求解JRD1和JRD2问题。本文DE求解流程分为以下四步[29]。为区分算法参数与问题参数符号，我们在算法参数上添加“～”。

1)相关参数设置和初始化过程

将参数划分成两类：问题相关参数和算法相关参数。问题参数设置参考相关研究实例，DE算法参数设置通常根据经验，具体过程是：

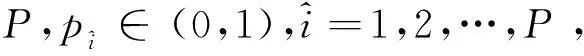
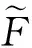
(16)

其中，pp=1,2,…,pop。把这些参数设置好后，转入下一步进行种群初始化。

2)初始化种群以计算适应度及目标函数值

种群初始化的结果就是生成当且最优解、最佳适应度、最佳适应度下染色体，这些参数用于DE算法的更新过程。如果我们定义算法种群为DP，则种群初始化为：

(17)

(18)

其中，‘round’用于四舍五入，rand(0,1)用于产生(0,1)之间随机数。由于我们以最低成本为目标函数，故令其为适应度函数。

3)基于DE的求解算法流程说明

为了更好的解释DE算法的流程，我们以一个2个产品、2个顾客的问题为例进行说明。

步骤1：变异操作。选择种群的第t代染色体作为变异的目标向量，随机产生三个不同的整数r1，r2，r3，分别代表种群的第r1、r2和r3染色体。如果预设F=0.6，整个变异过程如图3所示。如果变异出现基因异常，即用随机产生可行值代替。

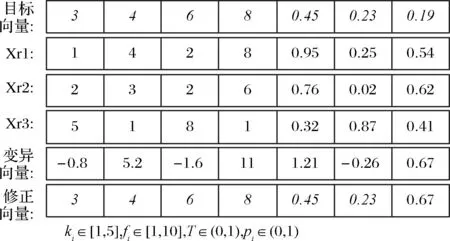
图3 变异操作示意图

步骤2：交叉操作。对每一个维度，随机产生一个长度为7(=2+2+1+2)的向量。如果randn(t)=4，CR=0.3，则根据交叉规则将生成新的染色体，如图4所示。

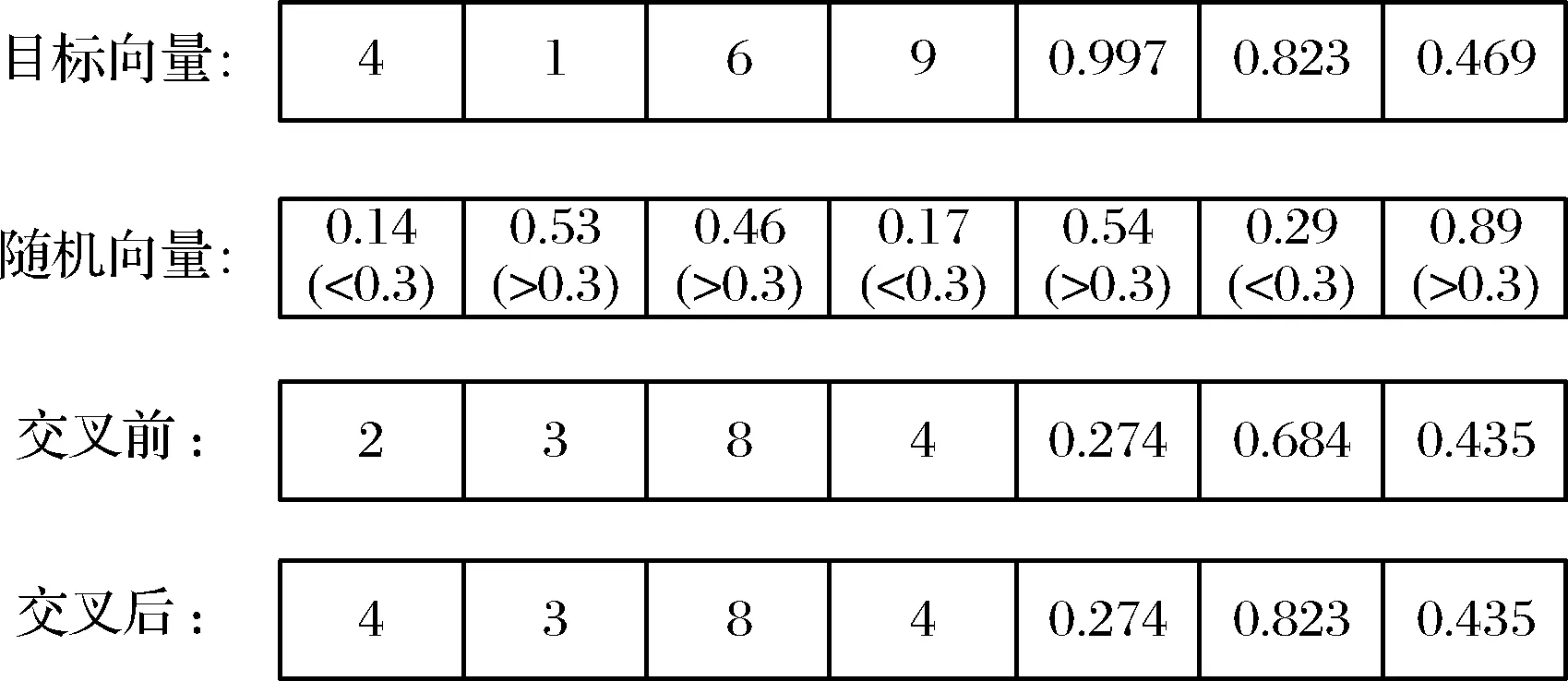
图4 交叉操作示意图

步骤3：选择及更新操作。根据贪婪选择规则，计算每个染色体的适应度，并输出当前最优适应度及当前最优染色体。

步骤4：重复步骤步骤1～步骤3，直至达到最大的迭代数量。

4)输出最优结果：当最大的迭代数量达到以后，DE算法即停止运行，输出最佳适应度、最佳适应度对应染色体以及最优解。DE算法求解流程图如图5所示。

4 数值分析与管理启示

本文数值分析部分主要包括两个内容，首先通过求解经典JRD问题，进行DE性能分析和算法参数的敏感性，之后用利用DE对JRD1和JRD2模型求解、分析问题参数的敏感性及RFID投资绩效。

4.1 DE算法参数设置

算法运行硬件环境为一台2.7 GHz CPU的个人电脑上，2 GB RAM，运行的软件环境为Windows 7 Home Premium，程序采用Matlab7.1编码。

1)对比算例测试

由于JRD模型的参数较多，也没有较为成熟的测试数据，本文采用Cha等[12]和Moon等[30]的算例进行测试，如表4。

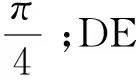
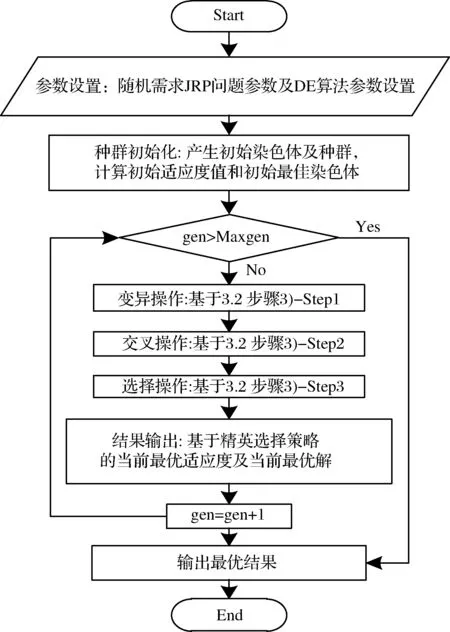
图5 DE求解流程

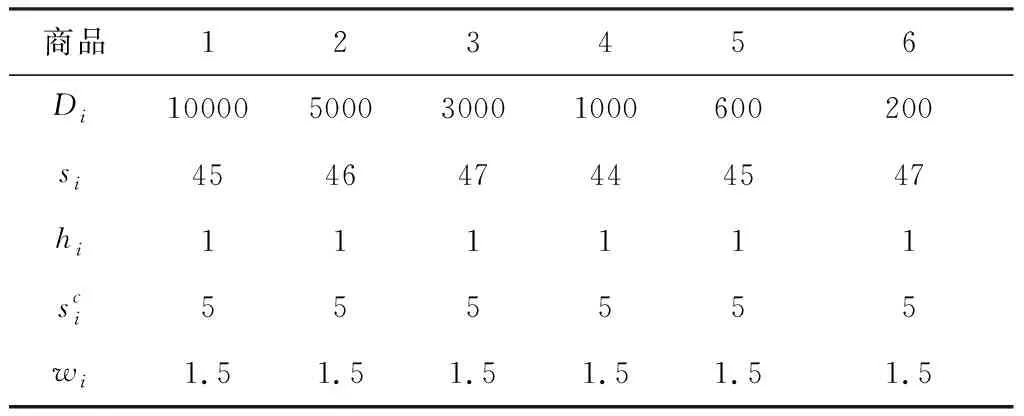
商品123456Di10000500030001000600200si454647444547hi111111sci555555wi1.51.51.51.51.51.5

表5 不同算法求解结果比较

其中，Error rate = (TC-optimal)/optimal ×100%。

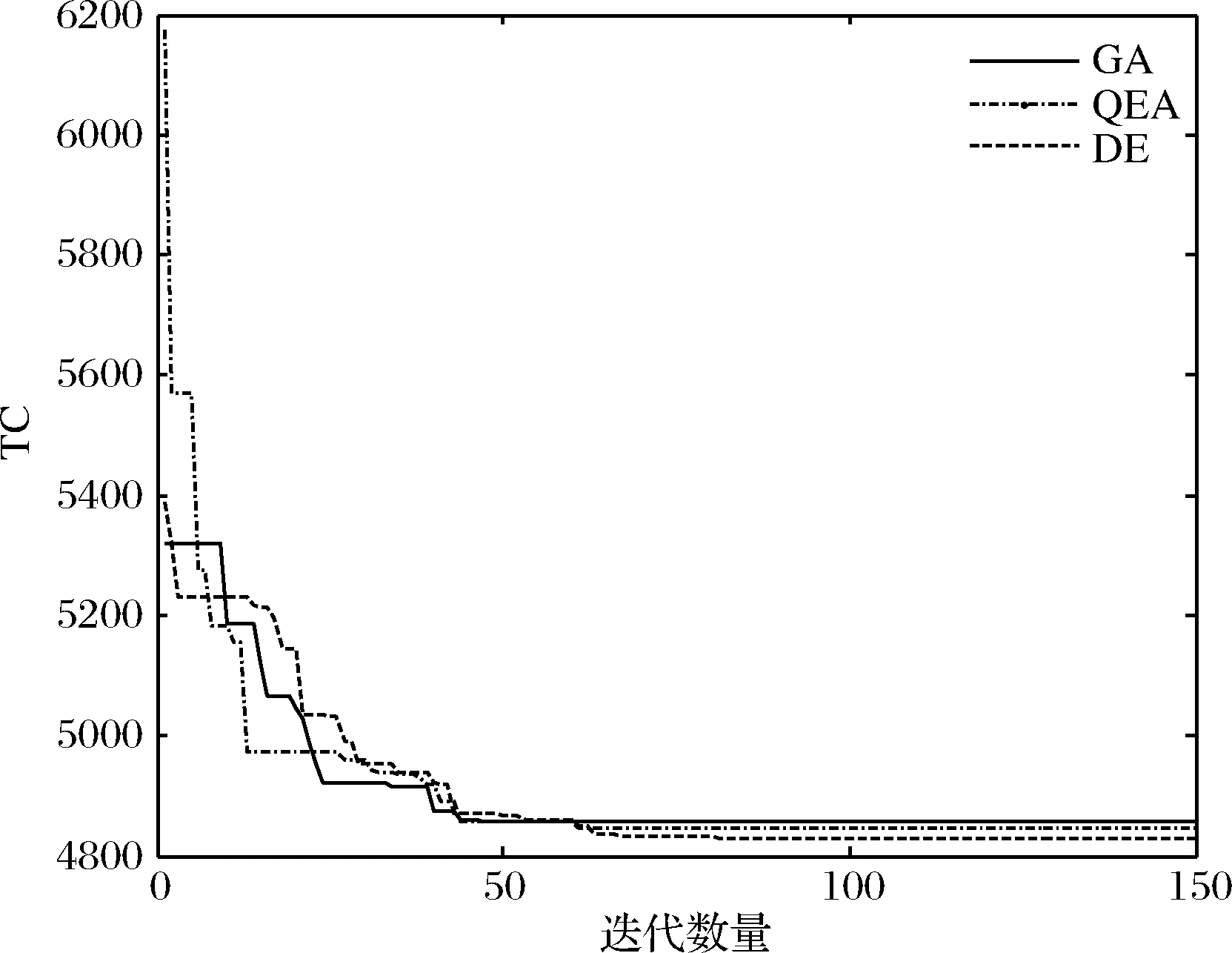
图6 三种算法的运算结果(GA, QEA, DE)

从表5和图6可知，DE进化算法在求解结果上明显优于GA和QEA，并且优于启发式算法SP-CC和SP-H。在求解效率上，DE算法的求解速度较快，能够较快的得到收敛。特别是和GA和QEA比较时，三种算法都在不足100代之内达到收敛，但是GA和QEA在100代内陷入了局部极值。三种进化算法在求解结果上，DE强于QEA，QEA强于GA；在求解速度上，DE强于GA和QEA，QEA与GA求解效率相近。实验表明DE算法用于求解JRD问题是可行的，下面将进一步对DE相关参数设置进行更深入的分析。

2) DE算法参数敏感性分析

DE算法的求解依赖于其变异算子Fc和交叉算子CR的设置。两个参数不同设置下求解JRD总成本结果如表6所示，其中总成本为每个参数组合下10次计算结果的均值。

表6 不同参数组合下DE算法求解TC 结果

按照表6给出的结果，DE算法在Fc∈[0.4,0.6]并且CR∈[0.2,0.8]的范围内，JRD都能获得最优值。这里取两者的中间值Fc=0.5，CR=0.5，以其作为下节求解JRD问题中DE算法的参数设置的依据。

4.2 模型求解及敏感性分析

4.2.1 算例与结果分析

在本文的JRD中，实例采用文献[31]给出的顾客数据，其中1≤p≤3，中心仓库和顾客的距离矩阵如表7所示，并假定单位运输距离成本cpm=0.1，参考Moon等[30]使用的6商品模型的数据，商品和顾客的匹配数据如表5所示，其中，‘0’表示该处无顾客发出订单，‘1’表示该顾客发出订单。

每个算法运行30次，迭代500次。求解JRD1的结果及进化过程如表9及图7所示。其中，‘0’表示中心仓库，其他数字代表顾客， AVE表示均值。

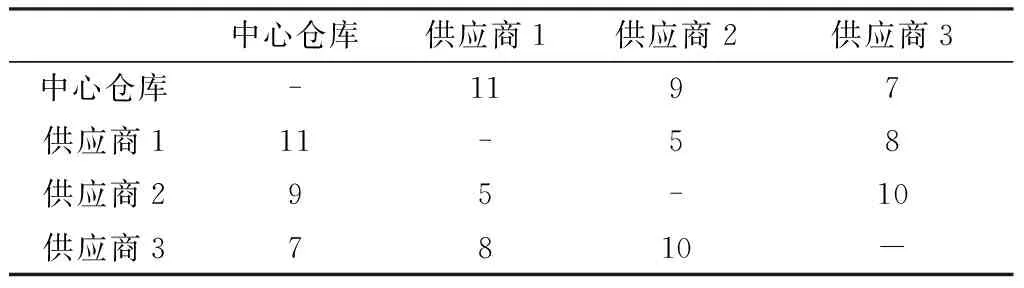
表7 相对距离 (公里)

表8 顾客和订单的匹配表

通过表9和图7可以看出，DE算法仍然能够在多个指标显示出优势，如收敛时间、收敛结果与收敛效率、求解平稳性(均值)，QEA算法次之，而GA求解效果最为一般。同时，DE算法还能给出最长的配送路径[0-2-1-3-0]。

表9 GA、QEA和DE计算JRD1问题的结果

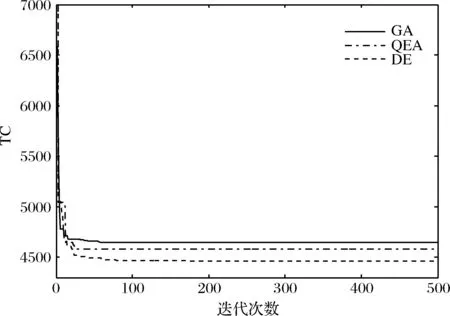
图7 三种算法求解JRD1问题的进化过程

4.2.2 RFID投资影响研究

1) JRD问题整体研究发现

根据Ferrer等[32]、Hsu[33]等和Nativi和Lee[34]对RFID的调查及评估结果，RFID能够提升30%的运作效率，甚至在某些环节能够达到100%。参考Lee和Lee[28]对RFID投资参数的设置情况，对RFID投资相关参数设置如下：U=1.0，V=0.7，M=1.0，N=0.7，λ=0.002，β=0.002。DE求解JRD1和JRD2问题的运行结果如表8所示，进化过程见图8。

表10 JRD1和JRD2问题的求解结果比较

其中，本文求得RFID投资参数为I=0.9249，CI=144.10，R=0.9247，CR=144.52。

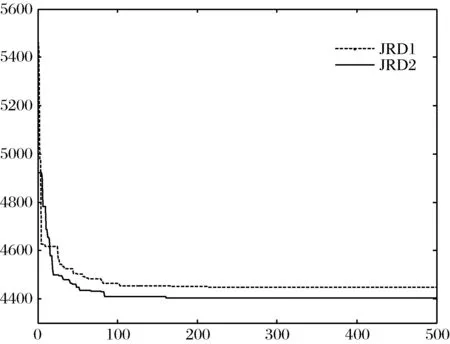
图8 DE求解两种JRD问题的进化过程

从表10可知DE求解JRD1和JRD2问题在求解效率上相差不多，JRD1稍微快一些。但是在求解问题的总成本下降为4402.66。也就是说，通过在订货效率上和JIT效率上投入RFID(总成本分别增加为144.10和144.52)，能够获得原来库存成本和顾客等待成本的0.9249倍，能够获得订货成本和运输成本的0.9247倍，两者结合考虑使得总成本降低4453.15-4402.66=50.49。

在图8中，JRD1收敛结果(总成本)明显结果要高于JRD2的收敛结果，这主要是由于RFID提效的结果。而两者的进化过程基本上是在200代左右即达到收敛，说明DE算法的进化过程是很快的。除了在整体上考虑RFID投资的效果，本研究将进一步考察不同的参数设置下RFID投资对JRD的影响。

2)JRD参数敏感性分析

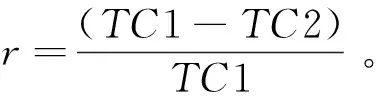
观察表11的结果，可得出以下结论：

① 从总成本变化率来看，随着参数的增大，RFID投资效果越来越明显。也就是说，在较高的成本参数下，投资RFID，所节约的成本是明显的，即需求量越大，库存成本越高、订货成本越高或者顾客的等待成本越高，实施RFID，效果越好。

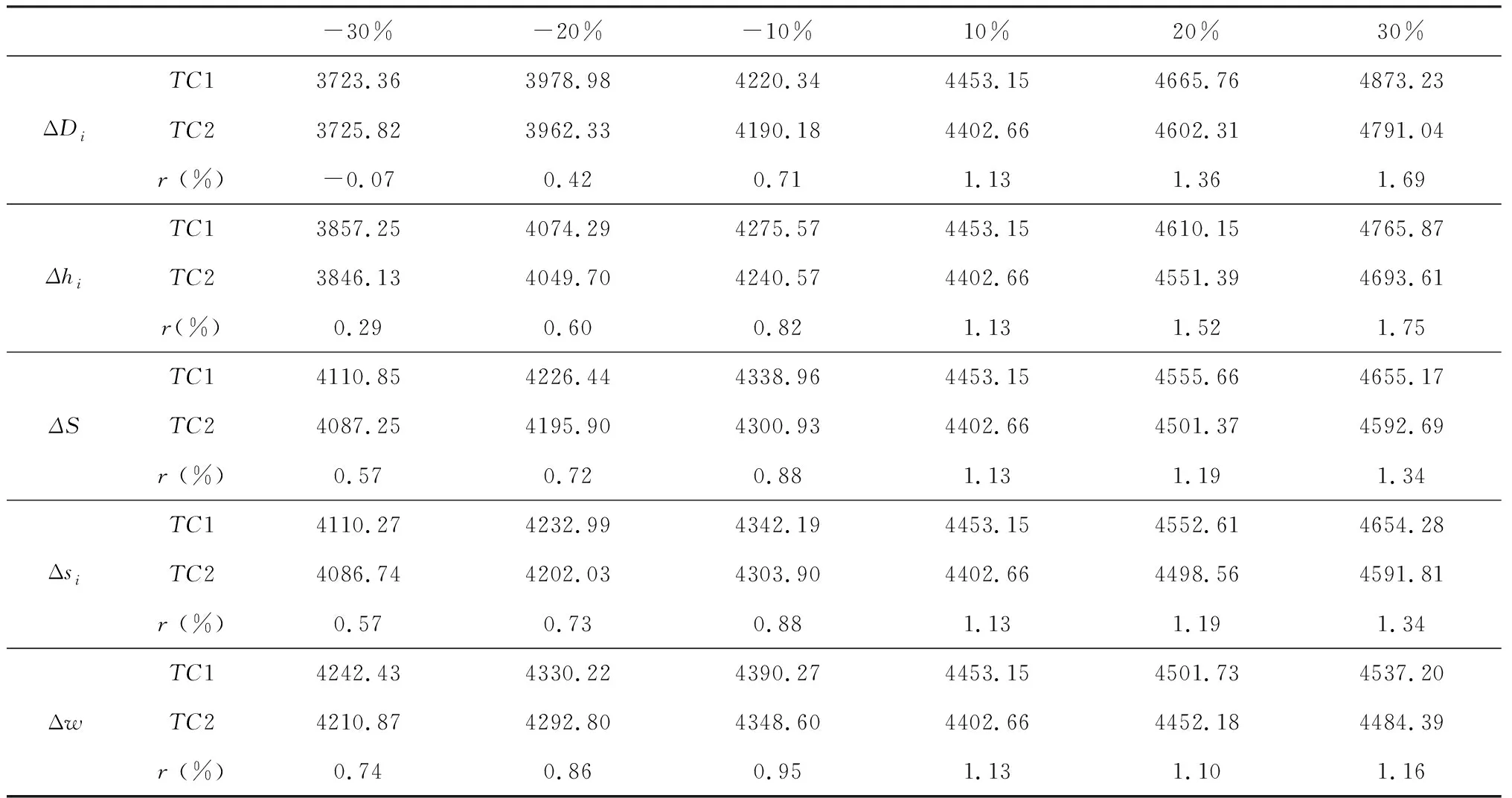
表11 不同参数设置下的JRD1 和JRD2求解结果

②从单个参数的变化来看，RFID投资对需求的影响最大(由负值逐渐变为正值)，对库存成本的影响次之，对顾客的等待成本影响最小。因此，加大在成本影响最大的领域投资，会得到较大收益。

③RFID投资对主要和次要订货成本的影响接近。因此在主要和次要订货成本给定的情况下，RFID投资影响与两者成本的比例关系的联系不大。

3)RFID投资参数分析

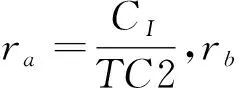
从表12中的数据，能够得到如下的结论：

①从整体上看，I或者R越大，表明成本变化越少，RFID在效率上体现的能力越低，在效率提升上所能投入的RFID成本也越低，如I= 1,CI= 0；I= 0.75,CI= 895.88，这符合实际的RFID投资情

表12 不同效率系数下JRD2的计算结果

况，即投资得越少，获得的收益越低，但是投资的多却未必获得较多的收益，如I= 0.75，TC2=4742.07超过TC1=4468.78。

②I和R相互影响，但是相互影响不大，特别是当某一种效率系数变动很大的时候，另一种效率系数波动不大，但是当某一种效率系数增大，另一种效率系数成下降趋势。

③当某一种效率系数增大时，其投资成本降低，但是总成本却是经历了先减后增的过程，在图像上凸向原点，即JRD系统最佳的投资点，也就是当TC2*=4402.66时的情况，此时I=0.9249，CI=144.10，R=0.9247，CR=144.52。

图9 不同I和R组合下TC2的变动趋势

由于I和R能够产生相互影响，故此我们想近一步观察一下在I和R相互影响下的JRD2总成本的情况。图9显示了不同I和R组合下的JRD2总成本的变动趋势。从图9显示的变化趋势，我们可以得到如下结论：

①I和R之间存在着最优效率组合，图9中显示为总成本的最低值在I=R=0.95处，TC2=4408.52。而根据我们的实际计算TC2的最优值为4402.66，此时I=0.9249，CI=144.10，R=0.9247，CR=144.52，I和R接近0.95。

② 图9中，TC2的变化趋势是先减后增的趋势，由I=0.75，R=0.75，RFID投资最多，TC2的最高；之后TC2逐渐下降到我们的最优值TC2=4402.66；再之后缓慢上升至无RFID无投资的情况，TC2=TC1=4453.15。

因此，从RFID投资的规模来看，RFID投资越大，获得的效率提升越大，I和R越小，但总成本并不是最低。可以认为RFID投资存在着一个合理的规模，而这个规模是由JRD系统效率提升后的总成本决定的，而由非单一流程效率改善后的JRD成本决定的。

5 结语

随着RFID在技术上的逐渐成熟，其应用将更加广泛。研究RFID对多品集采配系统产生的影响，有助于正确的评估RFID的收益，从而提升整个系统的运作效率和服务水平。在此基础上，本文通过协调JRD采配策略，建立了基于RFID的JRD投资决策模型，并设计了一种基于群体智能的DE求解算法。通过深入分析算例结果，得到以下三点有益的启示：

(1)基于RFID对订货效率提升和JIT效率提升的假设，RFID实施能够实现对改进的JRD问题总成本的降低。

(2)RFID在确定性需求JRD问题投资上存在着投资和回报的均衡。过高的RFID投资，在获得效率提升的同时也会导致总成本的增加，过低的RFID投资，使得系统效率提升有限，获得的成本节约也小于成本的指出。

(3)需求的规模、库存成本的高低、顾客等待成本的大小、以及配送策略及配送成本的高低都会影响RFID的实施效果。基本上成本越高的环节实施RFID的潜力越大，实施RFID后所获得收益也越高。

后续研究考虑运输过程中非线性运输成本，这样可使模型背景更贴近实际情况。此时，模型求解变得更为复杂，需要结合其他算法的优点，设计更为稳定、快速的混合DE算法进行求解。

参考文献：

[1] Shu F T. Economic ordering frequency for two items jointly replenished [J]. Management Science, 1971, 17(6): 406-410.

[2] Wang Lin, He Jing, Wu Desheng, et al. A novel differential evolution algorithm for joint replenishment problem under interdependence and its application [J]. International Journal of Production Economics, 2012, 135(1): 190-198.

[3] Khouja M, Goyal S. A review of the joint replenishment problem literature: 1989-2005[J]. European Journal of Operational Research, 2008, 186(1): 1-16.

[4] Wang Qinan, Axsater S. Fixed-interval joint-replenishment policies for distribution systems with multiple retailers and stochastic demand [J]. Naval Research Logistics, 2013, 60(8): 637-651.

[5] 聂佳佳，张娜娜．联合采购对存在强势零售商闭环供应链回收策略的影响[J]．系统管理学报, 2015, 24(1):98-106．

[6] 张云丰，王勇，龚本刚，等．非瞬时补货下改良品联合采购决策[J]．中国管理科学, 2016, 24(10):124-132．

[7] 李妍峰，李军，高自友．大规模邻域搜索算法求解时变车辆调度问题[J]．管理科学学报，2012,15(1):22-32．

[8] 刘艳秋，徐世达，张颖，等．考虑路径可行性与仓储集货模式下的回收车辆路径问题研究[J]．中国管理科学, 2016,24(12):98-107．

[9] 揭婉晨，杨珺，杨超．多车型电动汽车车辆路径问题的分支定价算法研究[J]．系统工程理论与实践, 2016, 36(7):1795-1805．

[10] Cetinkaya S I L, Mutlu F, Lee C. A comparison of outbound dispatch policies for integrated inventory and transportation decisions[J]. European Journal of Operational Research, 2006, 171(3): 1094-1112.

[11] Sindhuchao S, Romeijn H E, Akcali E, et al. An integrated inventory-routing system for multi-item joint replenishment with limited vehicle capacity [J]. Journal of Global Optimization, 2005, 32(1): 93-118.

[12] Cha B C, Moon I K, Park J H. The joint replenishment and delivery scheduling of the one-warehouse, n retailer system[J]. Transportation Research Part E: Logistics and Transportation Review, 2008, 44(5): 720-730.

[13] Qu Hui, Wang Lin, Zeng Yurong. Modeling and optimization for the joint replenishment and delivery problem with heterogeneous items[J]. Knowledge-Based Systems, 2013, 54: 207-215.

[14] Wang Lin, Dun Caixia, Lee C G, et al. Model and algorithm for fuzzy joint replenishment and delivery scheduling without explicit membership function [J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9-12): 1907-1920.

[15] Moon I K, Cha B C. The joint replenishment problem with resource restriction [J]. European Journal of Operational Research, 2006, 173(1): 190-198.

[16] Liao Weipang, Lin T M Y, Liao S H. Contributions to Radio Frequency Identification (RFID) research: An assessment of SCI-, SSCI-indexed papers from 2004 to 2008[J]. Decision Support Systems, 2011, 50 (2): 548-556.

[17] 冯芷艳，郭迅华，曾大军，等．大数据背景下商务管理研究若干前沿课题[J]．管理科学学报, 2013,16(1):1-9．

[18] Sarac A, Absi N, Dauz Ere-Peres S. A literature review on the impact of RFID technologies on supply chain management[J]. International Journal of Production Economics, 2010, 128(1): 77-95.

[19] Bottani E, Rizzi A. Economical assessment of the impact of RFID technology and EPC system on the fast-moving consumer goods supply chain[J]. International Journal of Production Economics, 2008, 112(2): 548-569.

[20] Szmerekovsky J G, Zhang Jiang. Coordination and adoption of item-level RFID with vendor managed inventory[J]. International Journal of Production Economics, 2008, 114(1): 388-398.

[21] 范体军，张丽，李琳，等．基于RFID技术的零售型供应链投资决策研究[J]．管理学报，2013,10(8):1230-1237．

[22] 范体军，张李浩，吴锋，等．RFID技术压缩提前期对供应链收益的影响与协调[J]．中国管理科学, 2013,21(2):114-122．

[23] 张李浩，范体军，杨惠霄．基于RFID技术的供应链投资决策及协调策略研究[J]．中国管理科学, 2015, 23(8):112-121．

[24] 张李浩，包兴，杨惠霄．供应链采用RFID的标签成本阈值分析及契约协调[J]．系统工程理论与实践, 2015, 35(5):1133-1143．

[25] 张永杰，张维，熊熊．投资策略与投资收益:基于计算实验金融的研究[J]．管理科学学报，2010, 13(9): 107-118．

[26] 张蕾，李敏强，赵秀云．内部控制监督最优投资分配模型及决策研究[J]．管理科学学报，2013, 16(7):34-44．

[27] 贺晓波，王冬梅，曾诗鸿．附碳汇收益的林业投资项目价值评估——基于实物期权定价理论[J]．中国管理科学, 2017,25(3):20-29．

[28] Lee I, Lee B C. An investment evaluation of supply chain RFID technologies: A normative modeling approach [J]. International Journal of Production Economics, 2010, 125(2): 313-323.

[29] 王林，顿彩霞，张金隆．基于混合差分进化算法的联合补货-配送优化模型[J]．中国管理科学, 2012,20(3): 86-93．

[30] Moon I K, Cha B C, Lee C U. The joint replenishment and freight consolidation of a warehouse in a supply chain [J]. International Journal of Production Economics, 2011, 133(1): 344-350.

[31] Wang Lin, Dun Caixia, Bi Wenjie, et al. An effective and efficient differential evolution algorithm for the integrated stochastic joint replenishment and delivery model [J]. Knowledge-Based Systems, 2012, 36: 104-114.

[32] Ferrer G, Heath S K, Dew N. An RFID application in large job shop remanufacturing operations [J]. International Journal of Production Economics, 2011, 133(2): 612-621.

[33] Hsu C I, Shih H H, Wang W C. Applying RFID to reduce delay in import cargo customs clearance process[J]. Computers & Industrial Engineering, 2009, 57(2): 506-519.

[34] Nativi J J, Lee S. Impact of RFID information-sharing strategies on a decentralized supply chain with reverse logistics operations [J]. International Journal of Production Economics, 2012, 136(2): 366-377.