航材需求为随机变量的订货批量模型建立与应用

刘臣宇，孙伟奇，李卫灵 （海军航空大学（青岛校区），山东 青岛266041）

航空兵部队在飞机训练中，航材经常会随机发生故障，当仓库没有库存备件时就需要临时订货。临时订货时有发生，这种临时需求是随机的，也就是说需求为随机变量。为了保证在随机需求发生时能尽快得到满足，不影响飞行训练，研究需求为随机变量时的订货批量模型至关重要。

1 模型建立

由于需求为随机变量，无法求得周期（即两次订货时间间隔）的确切时间，也无法求得再订货点确切来到的时间。但在这种多周期的模型里，在上一周期里没有用完的器材可以放到下一个周期里继续使用，故在这种模型里可以像经济订货批量模型那样，主要的费用为订货费和存贮费。我们可以根据平均需求像经济订货批量模型那样求出使得全年的P 订货费和存贮费总和最少的最优订货量Q*。即：（该模型是经济订货批量模型，这里不再推导。式中：c1为单位存储费，c3为每次订购费，D 为年需求量）。但在对再订货点的处理上与经济订货批量模型不同。

在经济订货批量模型中，由于需求率是个常量d（即每天的需求量），对于一个需要m 天前订货的情况，可以把再订货点订为d·m，即当仓库里还存有dm 单位的器材时，就再订货Q*单位的器材，这样当m 天后Q*单位的器材补充来时，仓库里正好刚好把剩余的dm 单位的器材用完，仓库及时得到补充。

而对需求为随机变量的情况，因为每天的需求是随机的，不是常量，这种处理显然是不恰当的，有时在这m天里需求大于m（这里为每天平均需求），这样在m 天里就出现了缺货，而有时需求小于m，这样m 天后当新的Q*单位的器材补充来时，仓库里还有剩货。

由于每次的订货量Q*可以按经济订货批量模型求得，每年的器材平均需求量可以很容易求得，这样就可以求出每年平均的订货次数，也可以以每年允许在m 天里出现缺货的次数来作为服务水平。可以依据事先制定的服务水平和m 天里需求量的概率分布来定出相应的r 值，并把r 值中超过m 的部分叫做安全贮存。

为需求随机变量的订货批量模型。

2 模型应用

某仓库直接从厂家购进B 器材，由于仓库与厂家距离较远，双方合同规定在仓库填写订货单后一个星期厂家把B 器材运到仓库，仓库根据以往的数据统计分析知道在一个星期里B 器材的需求量服从以均值μ=850 个，均方差σ=120 个的正态分布，又知道每次订货费为250 元，每个B 器材的成本为48 元，存贮一年的存贮费用为成本的20%，即每个B 器材一年的存贮费为48×20%=9.6 元，仓库规定的服务水平为允许由于存贮量不够造成的缺货情况为5%。仓库应如何制定存贮策略，使得一年的订货费和存贮费的总和为最少?

解：首先可以按经济订货批量模型来求出最优订货批量Q*，已知每年的平均需求量=850×52=44200 个／年，c1=9.6 元／个年，c3=250 元，得：

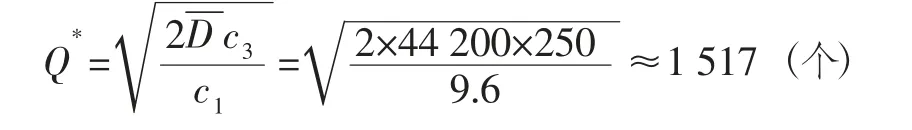
由于每年平均需求为44200 个，可知每年平均订货次数为

根据服务水平的要求：

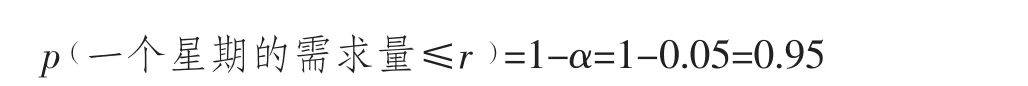
因为一个星期的需求量服从以均值μ=850 个，均方差σ=120 个的正态分布，故有：

查标准正态分布表，得：

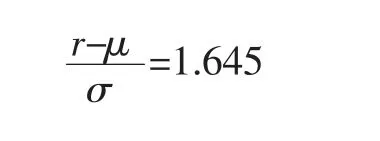
即有：

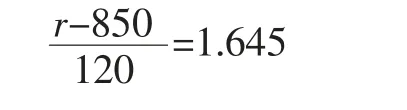
求得：

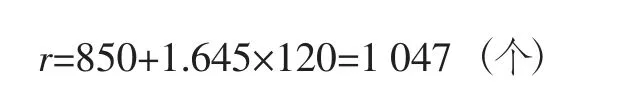
3 结 论

根据上例计算结果可知，当仓库里库存剩下1047 个时，就应该向厂家订货，每次的订货量为1517 个，这里的1047 就是再订货点，Q*=1517 就是最优定货量，而：

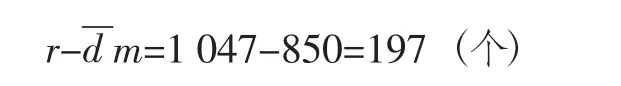
这197 个就是安全存贮量，在这样的存贮策略下，能有95%的概率在订了货而货物还没运到仓库的一周（简称订货期）里不会出现缺货。因为一年平均大约订货29 次，其中平均29×95%=27.55（次）的订货期里不会出现缺货，也只有平均1.45 次的订货期里会出现缺货。

当然在理想情况下，也就是一订货马上就能拿到器材，这时显然不需要安全存贮，每次订货量为850 个即可。