数学课堂中的放下与拿起——以“用字母表示数”为例

◇张 霞

一、放下应接不暇的目标，使本质意义凸显

最初选择 “用字母表示数”作为研究的课题，主要在于其多见，而且看了这么多年，还没看明白，始终感觉这节课内容多、目标多。就字母的意义来说，当前大家的课堂上就出现了表示“英文缩略、特定的数、任意的数、未知的数、变化的数”，含字母的式子可以表示“数量、数量间的关系、计算的过程、计算的结果”及“不同数量之间的相似关系”。不要说孩子，就是作为成年人的我都觉得很难把握这众多无序的意义。

什么是字母表示数的实质？翻读数学史，这句话点亮了我：“对应符号代数的历史发展过程，用来表示数的字母在具体意义上的历史演进过程为：记数→未知→一类”。［1］是啊，真正给数学史带来翻天覆地变化的正是用字母表示“一类数”这一意义，这一点也是学生今后学习代数学的基础。

所以，我将教学主目标定位在让学生领会字母表示一类数的内涵上。围绕这一目标，课堂中抓取的素材严格地限定在“数”的意义上。创设情境，让学生经历以前认识的数不足以表达无穷这一困窘，产生概括表达的需求；寻寻觅觅之后，找到新“数”——字母，体验字母概括、简洁地表示一类数的独特内涵；接着回顾旧知，联系用字母式子表示运算律、计算公式的经历，进行原因追踪，深化学生对字母表示一类数的认知；再从低年级学习中遇到的“扑克牌中的字母”、“算式中的‘字母’（如图 1）”，对字母表示数的意义进行扩充，了解其还可以表示 “特定的数、未知的数”；最后借用数学史中字母意义的变迁来梳理，使其各种意义有序化。为了能让学生在“字母表示一类数、含字母的式子表示数量关系”这些本质内涵上有深刻的体验和足够的探究时间，我决定暂缓字母式子的简写教学。

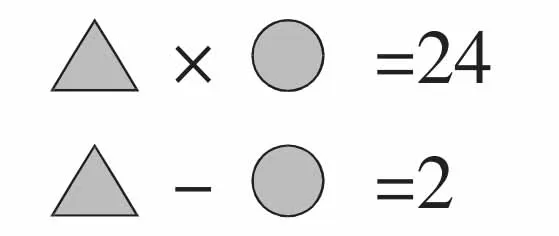
图1

二、放下眼花缭乱的情境，从“单一”中挖掘“多元”

不少课堂中，为了体现不同的教学目标，常常可以看到教师创设一个又一个情境。笔者以为，课堂中情境过多，课堂的整体感就降低，不利于学生课后回顾反思； 同时，不停地转换情境，也会分散学生的注意力。我们应尽可能地从同一情境中挖掘出多重的意义。

经过反复斟酌和课堂尝试，最终决定依据前期确定的主目标，借用“青蛙歌谣”这一个情境，通过把歌谣分段展现，让学生在概括歌谣过程中依次感受到“数的无奈”“文字的局限”，逐步找到并确认“用字母表示数”这一新方法，感受字母在概括表示一类数、简洁表达数量关系两方面的优势。

【教学片段】

1.展示儿歌的前半部分，在儿歌绵延不绝的叙述中产生数的概括表达需求。

师生共说儿歌，教师板书：“1 只青蛙1 张嘴，2 只青蛙 2 张嘴，3 只青蛙 3 张嘴。”

师：谁能继续说下去？ 都能啊！真好，那就请一位同学在黑板上继续写。

（一个学生写，教师安静地等待，叮嘱其一定要写完这首儿歌。要求其他学生边看边想：他写的和你想的是否一样？板书的学生终于不能再继续写了，在下面学生的提醒下，用“……”终结儿歌的书写）

师：为什么要画上省略号？

生：这是一首无穷无尽的儿歌。

师：是啊，一首无穷无尽的儿歌，如果要一句一句地写出来，怎么也写不完。我们难道就真的没有办法，把这无穷无尽的歌谣用一句话来概括？（等待片刻）请大家尝试写出自己的创造。

学生创造。教师在班上搜集的学生作品，主要有以下几类：（1000）只青蛙（1000）张嘴，（几）只青蛙（几）张嘴，（a）只青蛙（a）张嘴，（n）只青蛙（n）张嘴。

师：行吗？1000 可是一个很大的数呀！

生：不行，1000 再大，它也只能表示一种情况，不能把这无穷无尽的情况都概括进去。

师：用“几”来表示这无穷无尽的数，可以吗？

学生纷纷点头说：“行。”

师：青蛙的只数用“几”来表示，嘴巴的张数为什么也用“几”来表示呢？

生：青蛙的只数和嘴巴的张数是相同的。

师：噢，在同一情境里，同样的符号表示相同的数。

师：有的同学用字母a 来表示，也有同学用字母n 来表示，用字母表示一个数，可以吗？

（学生思考片刻后纷纷表示可以）

师：那这里的字母表示的是哪些数呢？

生：任何数。

生：任何自然数。

师：一首无穷无尽的儿歌，咱们同学找到用文字表示数、用字母表示数，轻而易举地用一句话把这绵延不绝的歌谣全部囊括，真棒！

2.展示儿歌的后半部分，通过创作难度的增大对比出字母表示数的优越性。

出示完整儿歌：“1 只青蛙 1 张嘴，2 只眼睛4 条腿；2 只青蛙 2 张嘴，4 只眼睛 8 条腿……”师生共说。

师：这样说下去，也是无穷无尽啊！你还能想出一句话，把这一整首歌谣都概括了吗？

学生创作。班上搜集的学生作品有以下几类，如图2：

图2

交流尝试单1、2。

师：我们都已经知道，用文字“几”或字母是可以概括这无穷无尽的自然数的。这种创造应该行吧？

（学生纷纷摇头）

生1：不行，相同的符号表示同样的数。

生2：不行，假如说这里的“几”表示6 的话，那么就表示“6 只青蛙 6 张嘴，6 只眼睛 6 条腿”了。

师：是啊，这样一来，天下的青蛙都残疾了！

（众生大笑）

展示尝试单3。

师：这下可以了吧，青蛙眼睛的只数、腿的条数终于和青蛙的只数不一样了！

（学生思考后纷纷摇头）

生3：还是不行。虽然青蛙眼睛的只数和青蛙只数不一样，但如果是4 只青蛙，6 只眼睛，怎么办？

师：是啊，如果每只青蛙的眼睛只数不一样，这个世界也很可怕啊！看来，不一样还不行，还得遵守规则。

师：我们这里有没有守规则的青蛙呢？

展示尝试单4、5。

生4：可以，青蛙眼睛的只数是青蛙只数的2倍，青蛙腿的条数是青蛙只数的4 倍。

生5：我觉得尝试单5 表达的意思更清楚，同时也简洁。

师：那好，我们就把尝试单5 记录下来。

（教师在黑板上记录）

3.回顾中感悟字母、含字母的式子表示数、数量关系的特点。

师：这里的a表示哪些数？

生1：1、2、3……这些自然数中的任意一个数。

师：真好，单独的一个字母a竟然表示了“1、2、3……”这样的无穷无尽的一类数。（板书：一类数）看看上面的 1、2、3……这些数，它们表示的是——一个数。（板书:一个数）

师：（指着“a×2”）这个含字母的式子表示的是哪些数啊？

生2：1、2、3……任何自然数。

生3：不对不对，这个式子表示的应该是2、4、6……这些自然数。

师：噢，“a×2”表示的是一个数还是一类数？那么这一类数和前面“a”所表示的那一类数是否相同？

生：（齐）不同。

生4：这一类是前面那类数的2 倍，从“×2”中清晰地看出来。

师:是啊，它们虽然都表示一类数，但是不同的“一类数”，“a×2”这个式子中清晰地表达了两类数之间的数量关系。（板书：数量关系）

4.对比中体验含字母的式子可以直接表示结果。

教师指着a×2 追问：在这里，青蛙眼睛的只数用a×2 这个式子来表示，而上面青蛙眼睛的只数用 2、4、6、8……来表示，咦，为什么不也用一个式子来表示呢？

生1：我们可以算出结果啊。

师：那么a×2 为什么不算出结果呢？

生：（笑）不好算啊，a可以取任何自然数。

师：正因为这样，在字母表示数的世界里，存在着一种我们以前没有接触过的形式——用式子来直接表示最后的结果。

小小的一首歌谣，一部分一部分地概括，逼出了对数的概括的需求，逼出了对表示数新方式的追寻；概括歌谣后一次又一次的对比，比出了“一类数”与“一个数”的区别，比出了“这类数”与“那类数”的区别与联系，比出了含字母的式子的多重意义。一个情境，多维目标，多重抵达。

三、放下反反复复的练习，在“一题”中抵达多维

苏教版教材“用字母表示数”的第一课时中设计的练习共6 道，其中1 道涉及简写，1 道让学生再次经历字母表示数的抽象过程，1 道是回顾面积公式并用字母表达，还有3 道则是不同问题情境中用字母和含字母的式子表示数量及数量关系。细读，有“套用已有的数量关系模式写出字母式子”、重形式轻实质之感。经过思考，我决定抓住字母表示“变化的数”及数量间“不变的关系”设计练习，让学生在对比选择中进一步深入体会字母表示数的意义。

【教学片段】

1.对比感受字母表示变化的数。

师：大家今年多大了？字母表示数有那么多的优点，为什么不说你们a岁了？

生：我们的年龄是11 岁，这是一个确切的数，不需要用字母来表示。

师：噢，我明白了，字母再好，也得用对地方，是这个意思吗？

（众生点头）

师：猜猜老师的年龄！告诉大家吧，老师今年的年龄是你们的3 倍还多6 岁。算一算，老师比你们大几岁？

生：28 岁。

师：去年你们多大？老师呢？明年你们多大？老师呢？

生：去年我们10 岁，老师38 岁；明年我们12 岁，老师 40 岁了。

师：看，随着时间的推移，我们的年龄都在不断变化。如果选择一个符号表示你们不断变化的年龄，你选择什么？（生：a）为什么不再用11来表示你们的年龄了？

生：年龄在不断变化，而11 只能表示一个数。

师：如果用a来表示你们的年龄，那么a可以取哪些数？

生：任何自然数。

生：我认为应该是1 到100 的自然数，因为人的年龄是有限的。

师：真好，人的年龄是有限的，我可不希望遇到一个千年老妖！

2.对比感受含字母的式子宜表示“不变的关系”。

师：如果用a表示你们的年龄，那么老师的年龄用下面哪个式子表示合适？

①a×3+6 ②a+28 ③以上两种都可以

（大部分学生选择③，个别学生选择①）

师：是不是真的这样呢？让我们试一试。当a=1 时，老师多大了？

个别学生脱口而出：9 岁了。

（众生笑）

师：（追问）笑什么？

生1：老师应该29 岁。

生2：年龄之间的倍数关系是变化的，不变的只有年龄差。

师：是啊，字母虽好，但用的时候还得选对关系啊。当a=7 时，你们牵着妈妈的手刚踏进小学校门时，老师多大了？

生：35 岁了。

师：如果用b 表示老师的年龄，你们的年龄用下面哪个式子表示合适？

①b÷3-6 ②(b-6)÷3 ③b-28

（学生都选择③，不再上当）

一道习题，从确切的数到变化的数，从变化的数量关系到不变的数量关系，学生在反反复复的对比中明晰字母表示数与以往的具体数之间的区别和联系，明白了选择字母式子表达数量关系的玄机。

以上谈的多是放下，只有放下了，我们才有空间拿起。拿起什么呢？拿起学生的“思维”，给予学生安静思考的时间，感受“数学是思维的体操”；拿起学生的“体验”，放手让其经历思维的磕磕碰碰、涂涂改改的过程，体验到“学习主体”的感觉；拿起学生的真实，真实的对话，真实的创造，让学生不在“让别人来帮忙”的支吾声中惊慌失措；拿起学生对数学学科的热爱，只有经历了“一种经过严肃认真的思考后豁然开朗的情感体验”［2］，数学课独有的坐思维过山车的惊险、快意才能让学生得之不舍。

究竟拿起什么？放下什么？关键还在于站得高看得远。站在知识系统的高点，辨其主要价值而取之；站在学生人生发展的远处，辨其长远意义而放大。