基于gAIC和滑动窗的自回归模型参数估计算法

杨淳沨 吴国成 伍家松 姜龙玉 孔佑勇 舒华忠

(东南大学计算机网络和信息集成教育部重点实验室， 南京 210096)(东南大学计算机科学与工程学院， 南京 210096)(东南大学中法生物医学信息研究中心, 南京 210096)

近年来，通过分析和处理大脑电信号来研究大脑连通性已成为脑工作原理和脑部重大疾病发生机制研究领域的热点之一[1-2].WGCI (Wiener-Granger causality index)算法[3]、DTF (directed transfer function)算法[4]、PDC (partial directed coherence)算法[5]等都可有效应用于研究大脑功能连通性和效应连通性[6].这些算法都是基于随机过程的自回归(autoregressive, AR)模型的算法，模型参数(阶数和系数)的估计起着举足轻重的作用.传统的AR模型阶数估计算法包括赤池信息准则(Akaike information criterion, AIC)[7]、最后预测误差法(final prediction error, FPE)和最小描述长度法(minimum description length, MDL)[8]等.这些算法均假设不同信号具有相同阶数.然而，在实际情况中，不同信号各自的阶数往往各不相同，因此这些算法会使模型项数过估计，从而导致后续的系数估计运算量加大且精准度不高.学者们继而开发了更加有效的AR模型参数估计算法[9-11].其中，最佳参数搜索(optimal parameter search, OPS)算法[12]是一种鲁棒性较高的算法，即使在存在噪声且模型初始阶数选取不当的情况下，OPS算法仍能筛选出正确的模型项.但是，在干扰项较多的情况下，OPS算法的性能下降较快，从而会产生较大误差，导致难以筛选出所有正确的模型项.

本文提出了一种基于gAIC (generalized AIC)[13]和滑动窗的自回归模型参数估计算法.其中，模型的阶数估计采用gAIC算法，与AIC相比，它能更有效地减少干扰项数目.对原始信号进行加窗处理，可以消除部分信号的不稳定性.实验结果表明，相比传统算法，所提算法在模型参数估计方面具有更好的鲁棒性.

1 模型参数估计算法

对于一个平稳时间序列y,y(n)表示其在n时刻的值.如果已知时间序列y在某一时刻n之前p个时刻的值，可以建立一个基于该时间序列过去p个值的自回归模型，并且可用该模型来预测该时间序列将来的值，即

(1)

式中，p为该线性自回归模型的阶数；ai为y(n-i)项的系数；e(n)为真实值和预测值之间的误差项.

若在单变量的基础上引入另一个平稳时间序列x，可建立二维自回归模型，即

(2)

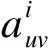
1.1 自回归模型的模型阶数估计算法

模型阶数估计是自回归模型参数估计过程中的重要步骤.赤池信息准则[7]是常用的模型阶数估计算法，它是一种基于信息论的算法，主要思想是在模型与数据的拟合精准度和模型复杂度之间进行权衡，得出模型的最优阶数.

给定一个零均值的m维向量自回归过程zn={zn(1),zn(2),…,zn(m)}T，即

(3)

式中，Φi(i=1,2,…,p)为m×m的系数矩阵；wn为零均值独立同分布的向量.假定对于任意的变量i>0，wn和zn-i是相互独立的.

假设观测值z1,z2,…,zN都是由式(3)中的自回归过程所产生，其中N为序列的长度.为了求得模型阶数p的估计值q，设定一个估计阶数的最大上限K，令q取1～K中所有整数值.对于每一个q值，均采用最小二乘法对原模型进行估计，得到如下模型：

(4)

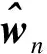
ZAj=zq+1,jj=1,2,…,m

(5)

式中

式中，Φi(j)表示Φi的第j行.

利用最小二乘法求解式(5)可得

(6)

原模型的预测误差协方差矩阵可表示为

(7)

采用AIC定义式选择最优的阶数估计q，即

(8)

令q取遍1～K中所有整数值，当AIC(q)值最小时，对应的q值即为该模型的最优阶数.

对于一个二维自回归模型(见式(2))，由式(8)可知，AIC算法是在假定自回归模型中不同信号具有相同阶数的基础上进行估计的，即q=qxx=qyx=qxy=qyy.然而，在实际情况中，自回归模型中不同信号的阶数往往各不相同，AIC算法会在估计模型阶数时产生过估计，导致后续系数估计运算量加大且精准度不高.针对这一问题，本文采用另一种改进的模型阶数估计算法gAIC[13],其定义如下：

(9)

1.2 OPS算法

以式(2)中的时间序列y为例，可得

(10)

采用OPS算法时，首先从式(10)模型项所组成的候选向量中筛选出线性无关项.这些候选向量所构成的矩阵表示为

[V1V2…Vqyy+qxy]T

(11)

式(11)中每一行代表一个候选向量.选择V1作为第1个选出的向量，判定下一个候选向量V2和V1是否线性无关，即利用V1来拟合V2，并计算V2和估计向量的误差值.一般情况下，在无噪声的信号中，向量之间应该是线性无关的.但是在有噪声的情况 (即误差不为零) 下，可以设置一个最大误差值，当误差值小于该最大值时，向量V2便可被选为线性无关的向量，反之则丢弃向量V2.选出V2作为极大线性无关组中的另一个候选向量后，采用向量V1和V2来估计V3的线性无关性.重复以上步骤直到选出一个新的候选向量组合φ=[ω1ω2…ωR]，其中R为所选出的线性无关向量总数.

筛选出新的线性无关的候选向量后，对其进行最小二乘法处理，即将式(10)改写为

(12)

式中

θg={g1,g2,…,gR}

(13)

式中，gi(i=1,2,…,R)为模型系数.为了最小化误差ey(t)，令下式达到最小值：

(14)

然后利用最小二乘法可得

(15)

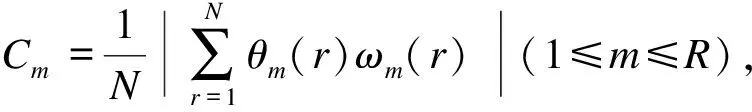
1.3 自适应OPS算法

对于1.2节中的OPS算法而言，确定候选向量集合，即式(11)中行向量所形成的矩阵，是一个非常重要的过程.AIC准则存在过度拟合的问题，且对二维自回归模型的每个维度得到相同的阶数估计值，因此，本文采用gAIC算法对自回归模型进行阶数估计，得到每个维度的各自阶数，继而进行后续计算.另一方面，考虑到OPS算法对于噪声敏感，为了减少噪声的影响，对原始信号进行重叠加窗处理.以式(10)为例，对于一个长度为N的信号，选择一个宽度为W的滑动窗，其滑动步长L，具体步骤如下：

①从信号中提取长度为W的信号，记为Wi；

②对每段窗信号Wi，利用gAIC估计出模型阶数，得到式(11)中的矩阵V，进而使用OPS算法计算矩阵V中每个候选项的权重值；

③将窗向后滑动一段距离L；

⑤计算式(4)中T个窗信号每个候选项权重的均值，并以此作为该候选项的权重值，对候选项进行最终筛选.

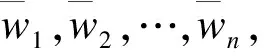
2 实验结果及分析

实验中采用了如下的二维自回归模型：

(16)

式中，ex(n)和ey(n)表示均值为0、方差为1的相互独立的高斯白噪声序列.

为比较OPS算法和自适应OPS算法的效果，进行了1 000组实验，并将结果应用于式(16)y(n)的参数估计中.在OPS算法中，为了考察模型阶数过大情况下算法的性能，需预设一个比实际情况大的阶数上限.针对本文实验中所用模型，该阶数上限设为10.由1.2节可知，模型阶数越大，候选向量越多，从而导致计算量越大.针对这一问题，分别采用AIC和gAIC算法进行阶数估计，以减少不必要的计算.由AIC得到的估计结果为6，即候选项为Y(n-1),Y(n-2), …,Y(n-6),X(n-1),X(n-2), …,X(n-6)，从而将候选向量个数由20降至12.采用gAIC算法对模型阶数进行估计，得到的阶数qyy=6，qxy=3，即候选项为Y(n-1),Y(n-2), …,Y(n-6),X(n-1),X(n-2),X(n-3).然后，考虑加窗处理对OPS算法估计模型阶数正确率的影响.由此设计了6种组合实验方案，见表1.

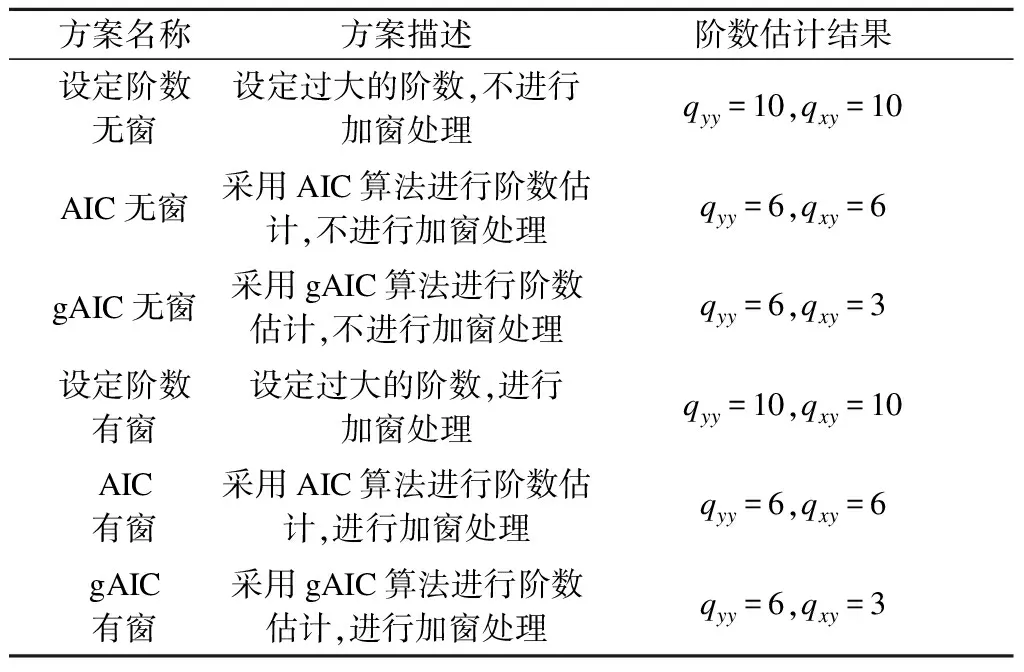
表1 6种组合实验方案

下面以表1中第6种组合实验方案为例，说明模型阶数的选取过程.首先，由gAIC算法得到信号y(n)中的模型阶数qyy=6，qxy=3.然后，由第1节中所述算法求得每个候选项的权重值，结果见图1.图中，候选项的权重值表示每个候选项的重要程度，按递减顺序排列.由图可知，X(n-3)项的权重值最大.按照1.2节所述筛选候选项的原则，权重值前四大项(即X(n-3)，Y(n-6)，X(n-1)，Y(n-5))相加之和已超出预先设定的阈值0.92，这4项即为最终需保留的候选项.其余5项的权重值较小，接近于0，表明其对信号Y的贡献可以忽略不计，该结果与式(16)中模型一致.

图1 各候选项的权重值

为了验证算法对不同长度信号的有效性，对于表1中的6种方案，每种方案选取2种不同长度(1 000和500)的信号，分别进行1 000次实验.对于长度为1 000的信号，滑动窗长度为800，步长为40；对于长度为500的信号，滑动窗长度为300，步长为40.考虑到OPS算法需要阈值，而阈值选取没有统一标准，因此，本文采用不同阈值进行实验.实验结果见图2.实验结果中的正确定义为算法筛选出完全正确的4个候选项，多选和少选都归为错误.由图可知，大部分阈值范围(除高阈值范围)内，有窗情况都明显优于无窗情况；在同样有窗/无窗情况下，gAIC算法的正确率均高于其他2种算法.N=1 000时最佳阈值约为0.92，N=500时最佳阈值约为0.88，正确率均接近90%.当信号长度从1 000减少到500时，OPS算法仍具有较好的性能，如gAIC加窗方案，最佳阈值不同，但正确率并未明显下降，均接近于90%.

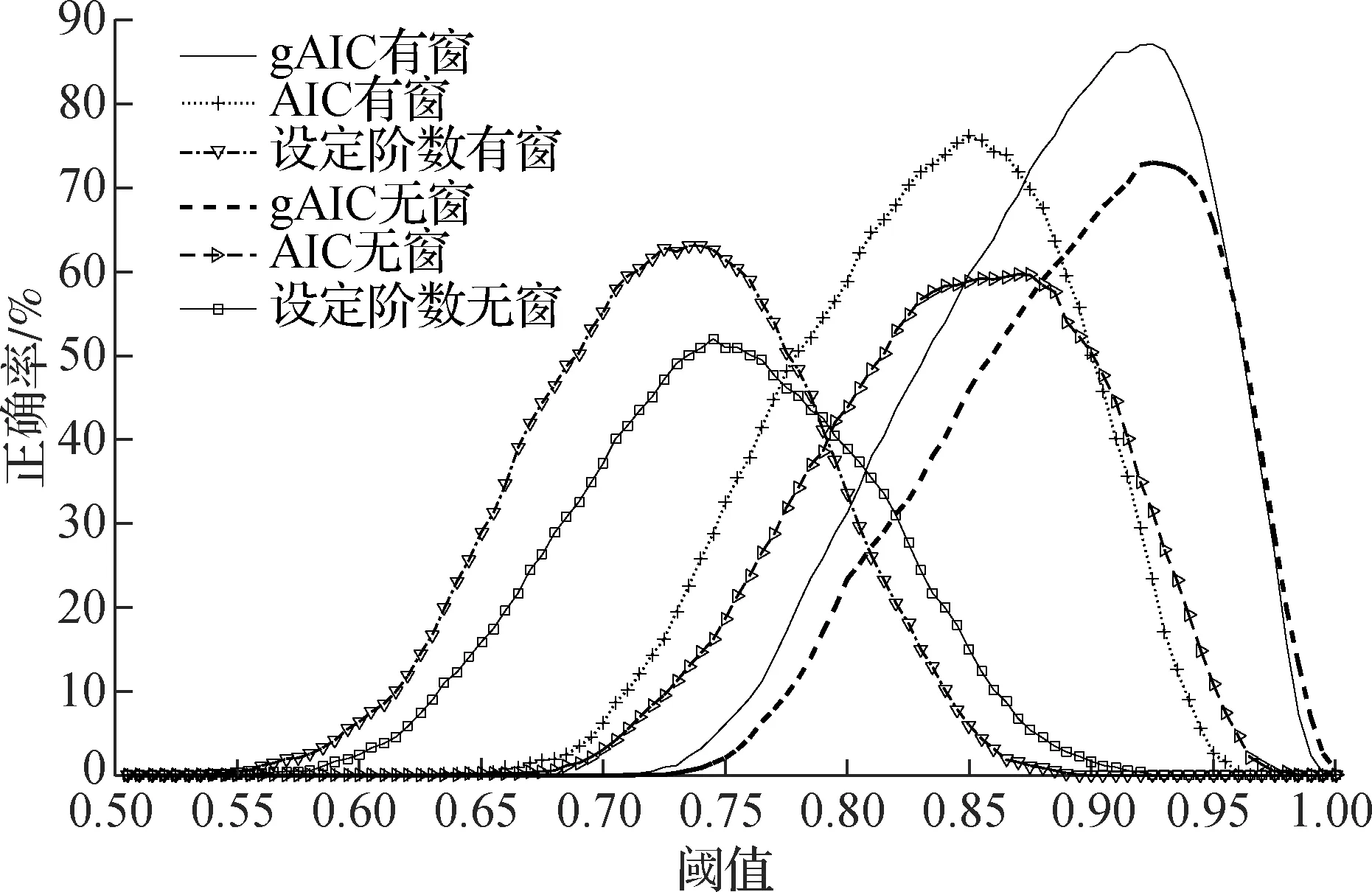
(a) N=1 000

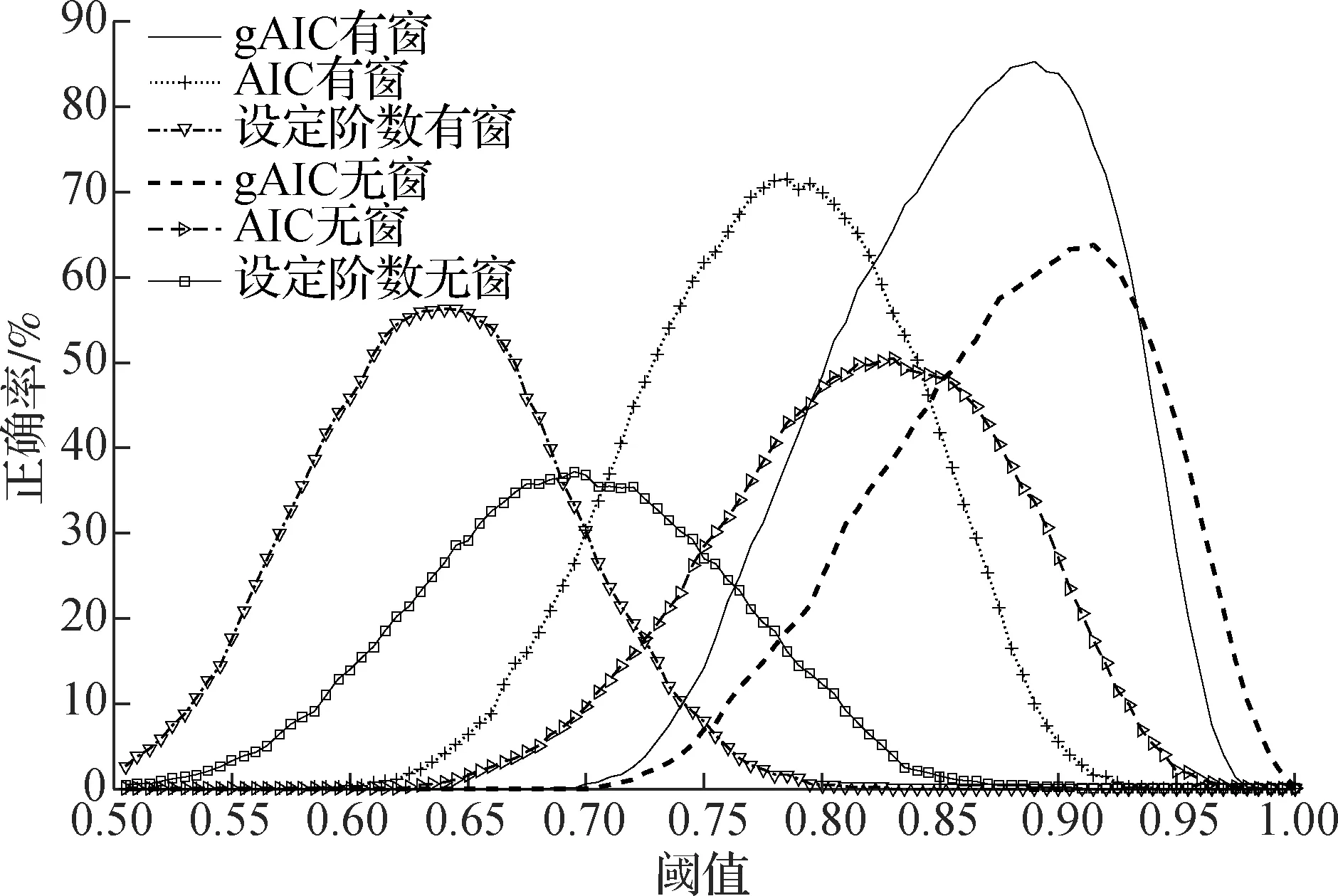
(b) N=500图2 不同阈值下6种方案结果对比

图1中，Y(n-5)项之后候选项的投影值较前4项大幅减少，可以认为候选项集合被分成2个部分，即图中前4项和后5项.由图2可知，阈值较大时，算法的正确率急剧降低至0，根据OPS算法，当阈值慢慢增大直到1时，包含的候选项增加，即逐渐将剩余的权重值较小的候选项全部选入.由此可知，阈值的选取对算法的正确率起着至关重要的作用.因此，采用了1.3节中的自适应OPS算法选取最优阈值.对于图1中按权重值降序排列的9个候选项，依次计算相邻2项的比值，结果见图3.由图可知，比值为Y(n-5)/X(n-2)时权重值取得最大值，其后项的权重值显著降低.因此，仅保留前面4项.

自适应OPS算法的实验结果见图4.实验中信号长度为1 000.由图可知，gAIC有窗的实验方案取得了最高的正确率，这与图2(a)中的结果一致.

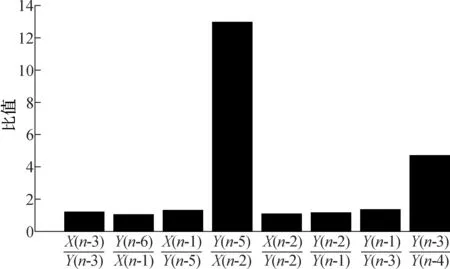
图3 相邻2项权重值的比值

综上可知，通过在算法中引入gAIC，可以有效减少实验过程中候选项集合里干扰项的个数；采用加窗的方式，信号能更加平滑，从而减少噪声带来的影响.这2种改进均能使OPS算法的正确率明显提升.自适应OPS算法的正确率较gAIC有窗方案有所下降，但其计算过程中不需要阈值，尤其适用于没有先验知识的数据或模型.

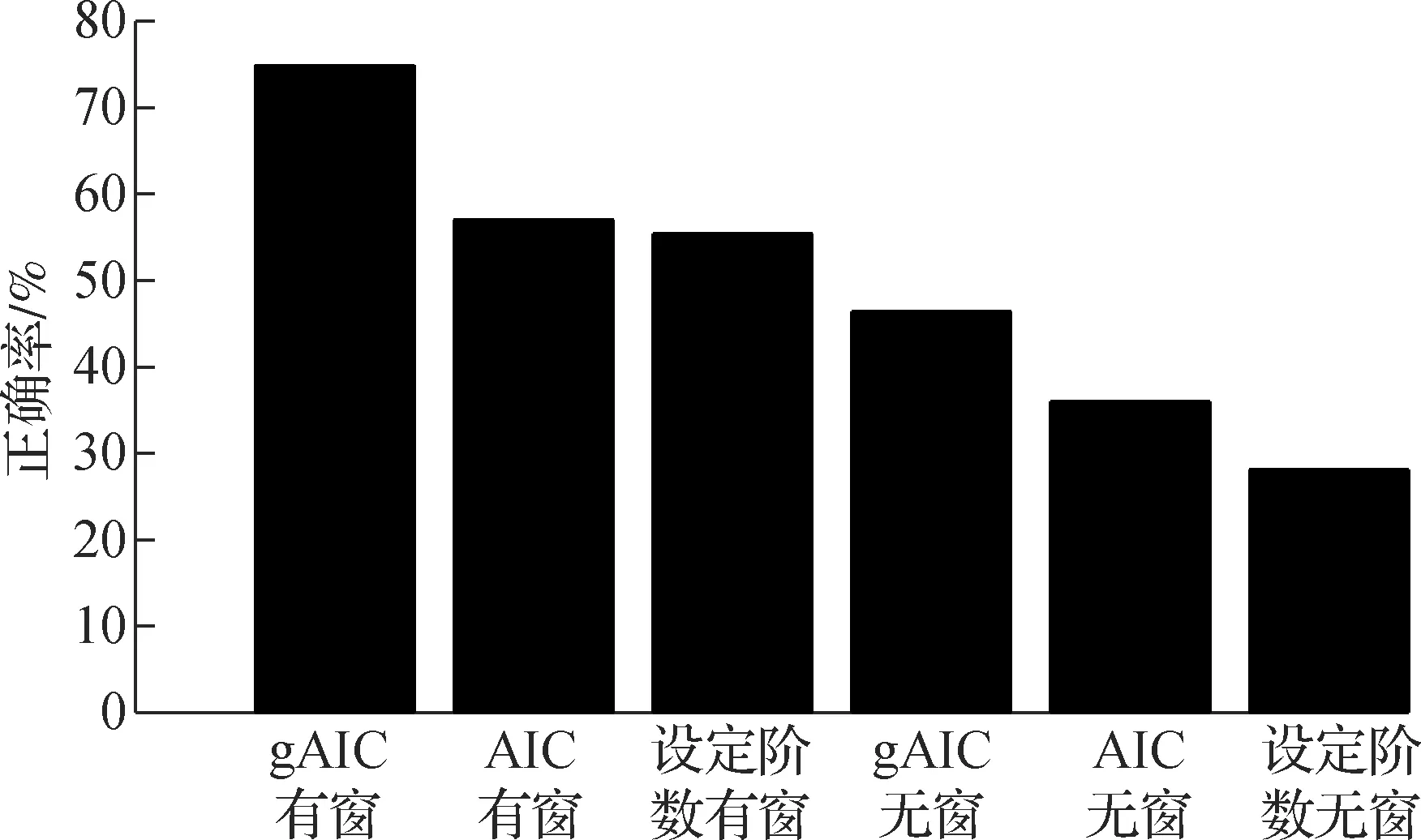
图4 自适应OPS算法的实验结果

3 结论

1) 针对自回归模型参数估计问题，本文提出了一种基于gAIC和滑动窗的模型参数估计算法.

2) 在模型参数估计中，使用gAIC算法对模型阶数进行估计，从而有效减少模型中候选项集合里干扰项的个数.然而，对信号进行加窗处理，使得信号能更加平滑，减少噪声带来的影响.最后，采用自适应OPS算法，进一步筛选候选项集合中的候选项，得到最终的模型选项及相应的模型系数值.

3) 实验结果表明，对于2种不同的实验信号长度，6种组合实验方案下所提算法都表现出最优的鲁棒性，其正确率接近于90%.

参考文献(References)

[1] 蒲慕明, 徐波, 谭铁牛. 脑科学与类脑研究概述[J]. 中国科学院院刊, 2016, 31(7): 714,725-736. DOI: 10.16418/j.issn.1000-3045.2016.07.001.

[2] Sporns O. Brain connectivity [EB/OL]. (2007-10-27)[2017-05-10]. http://scholarpedia.org/article/Brain_connectivity.

[3] Granger C W J. Investigating causal relations by econometric models and cross-spectral methods [J].Econometrica, 1969,37(3): 424-438. DOI: 10.2307/1912791.

[4] Kamiński M J, Blinowska K J. A new method of the description of the information flow in the brain structures[J].BiologicalCybernetics, 1991,65(3): 203-210. DOI: 10.1007/BF00198091.

[5] Baccalá L A, Sameshima K. Partial directed coherence: A new concept in neural structure determination[J].BiologicalCybernetics, 2001,84(6): 463-474. DOI: 10.1007/PL00007990.

[6] Friston K J. Functional and effective connectivity:A review[J].BrainConnectivity, 2011,1(1): 13-36. DOI: 10.1089/brain.2011.0008.

[7] Akaike H. Power spectrum estimation through autoregressive model fitting[J].AnnalsoftheInstituteofStatisticalMathematics, 1969,21(1): 407-419. DOI: 10.1007/BF02532269.

[8] Rissanen J. A universal prior for integers and estimation by minimum description length[J].TheAnnalsofstatistics, 1983,11(2): 416-431. DOI:10.1214/aos/1176346150.

[9] Khorshidi S, Karimi M, Nematollahi A R. New autoregressive (AR) order selection criteria based on the prediction error estimation[J].SignalProcessing, 2011,91(10): 2359-2370. DOI:10.1016/j.sigpro.2011.04.021.

[10] Zhao Y, Billings S A, Wei H L, et al. A parametric method to measure time-varying linear and nonlinear causality with applications to EEG data[J].IEEETransactionsonBiomedicalEngineering, 2013,60(11): 3141-3148. DOI: 10.1109/TBME.2013.2269766.

[11] Stoica P, Babu P. Model order estimation via penalizing adaptively the likelihood (PAL)[J].SignalProcessing, 2013,93(11): 2865-2871. DOI: 10.1016/j.sigpro.2013.03.014.

[12] Lu S, Ju K H, Chon K H. A new algorithm for linear and nonlinear ARMA model parameter estimation using affine geometry[J].IEEETransactionsonBiomedicalEngineering, 2001,48(10): 1116-1124. DOI: 10.1109/ 10.951514.

[13] Yang C, Le Bouquin Jeannes R, Bellanger J J, et al. A new strategy for model order identification and its application to transfer entropy for EEG signals analysis[J].IEEETransactionsonBiomedicalEngineering, 2013,60(5): 1318-1327. DOI: 10.1109/TBME.2012.2234125.