输电杆塔在风沙荷载激励下的动力响应分析

张卓群 李宏男 李士锋 默增禄 郝 鑫

(1大连理工大学建设工程学部, 大连 116024)(2国核电力规划设计研究院有限公司, 北京 100095)

输电铁塔结构具有塔身高耸、杆件众多、结构动力响应复杂等诸多特点[1-2]．目前，我国电网体系正在逐步完善，越来越多的输电线路需要穿越大风区、重冰区、高烈度区、高海拔区、多风沙区以及多种不良地质条件区域．针对不同的灾害形式和荷载组合，如何有效地提高输电线路整体的安全等级、保证持续送电时长和防灾减灾能力等一直是电力行业研究的重点和难点．

沙尘暴灾害是风沙危害的一种重要表现形式，也是对输电线路安全性威胁较大的自然灾害之一[3-4]．沙尘暴是一种常见的自然现象，多发生于我国西北、华北和东北等地区[5]，在输电塔结构设计中风沙荷载通常被忽视．近年来，我国多次发生特大沙尘暴，不仅波及范围越发广泛，造成的损失也愈发严重．2000年3月，大面积沙尘暴天气发生在我国内蒙古自治区，局地甚至出现8～9级的瞬时风力．我国北方地区在2002年3月发生了1990年以来影响最恶劣、强度最大、范围最广、持续时间最长的沙尘天气，波及范围多达140×104km2．2010年4月，我国冀东南地区多个县市发生沙尘暴灾害，部分地区能见度小于500 m．2015年4月，我国西北、华北大部分等地均出现了扬沙浮尘天气．其中，北京地区时隔13年后再次出现强沙尘暴天气，部分区域瞬时风力达到9级．沙尘暴灾害不仅给人们的生活带来诸多不便，也对风振敏感度极高的输电塔线路造成了巨大影响．

虽然风沙危害对输电杆塔具有明显的风蚀效应，但是关于风荷载携带沙粒后共同作用于杆塔结构所造成的危害则缺乏深入研究，针对风沙荷载的破坏程度和等级尚无定论．输电线路对风荷载具有极强的敏感性，随着沙尘暴荷载强度的升高，风沙耦合效应对输电杆塔产生的影响逐渐增大，甚至可能导致杆件破坏．本文基于动量守恒定律和沙尘暴天气等级理论，建立了风沙荷载力学计算模型．通过Matlab软件分别对风和风沙荷载进行模拟，并采用SAP2000软件对不同荷载作用下的输电塔结构动力响应差异进行分析，最终求解出不同等级沙尘暴对输电铁塔的危害．

1 风沙荷载

1.1 沙粒荷载

1.1.1 沙粒荷载分类

沙粒荷载的类别和分类比较复杂，本文以沙尘浓度作为沙粒荷载分类的主要依据．沙尘浓度是评判沙尘暴强度的一个重要因素，也是衡量风沙流所能携带沙粒量的重要参数．根据文献[5-6]和各地观测值的综合分析数据可知，不同强度的沙尘天气下，地面沙尘浓度的综合值是不同的，具体参数见表1．

表1 沙尘暴颗粒浓度计算参数

1.1.2 沙粒荷载计算

根据动量守恒定律和已有试验研究结论[7-9]，沙尘暴灾害发生时，沙尘颗粒撞击挡风结构的计算公式为

(1)

式中，Fs(τ)为τ时间内沙尘颗粒流体对挡风结构的撞击力；m为τ时间内撞击挡风结构的沙尘颗粒质量；v1，v2分别为强风流中单位体积沙尘颗粒撞击结构前、后的速度．

虽然沙粒撞击铁塔构件表面时存在明显的冲蚀磨损现象，但是构件表面有镀锌层保护，因此冲蚀磨损破坏对构件承载力无影响，风沙荷载计算时可忽略不计．因此，为简化计算，假定沙尘颗粒撞击输电塔构件为一种弹性碰撞，且反弹后的速度与撞击前的速度一致，即

v1=-v2=vs

(2)

式中，vs为强风流中单位体积沙尘颗粒的平均飞跃速度．

式(1)可转化为

(3)

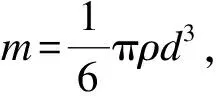
(4)

式中，mi(i=1,2,…,N)为沙粒i的质量．

在单位体积内，假设所有沙尘颗粒均作用在输电塔结构上，则某一直径的沙尘颗粒荷载作用力之和为

Fi=F(τ)ni

(5)

式中，Fi为τ时间内沙粒i的荷载作用力之和；ni为沙粒i在τ时间内作用在输电塔结构上的数量．

时间τ内经过输电塔杆件的流体体积为

V=2Al

(6)

式中，l为流体在时间τ内经过的距离；A为输电塔杆件迎风面面积．鉴于输电铁塔的镂空式结构、沙尘颗粒的离散性以及偏于安全的简化计算思路，假定输电塔前后侧迎风面均遭受到沙粒荷载的冲击作用，将结构的受力面积简化为2A．因此，沙尘颗粒荷载为

(7)

根据《沙尘暴天气等级》并参考文献[5，8]，输沙强度观测系统中某一高度h处的积沙量为

Qh=∑ρTSPAsVhT

(8)

式中，ρTSP为大于起沙风速情况下某一风速所对应的风沙流密度(即总悬浮微粒密度)；As为输沙强度观测系统的集沙器进沙口面积；Vh为高度h处风沙流密度所对应的风速；T为在取样时间内起沙风所持续的时间．

由式(7)和(8)可知

(9)

则沙尘颗粒荷载的计算公式为

Fs(t)=4ρTSPvs(t)2A

(10)

1.2 风荷载模拟

对于输电线路、高耸结构、高层、超高层建筑、房屋、桥梁等，风荷载都被视为一种重要的控制荷载[10-12]．在某一高度处，某一点上的风速度均可表示为平均风速与脉动风速之和．其中，平均风速具有沿高度变化的规律；脉动风对结构的作用是随机的，应按随机振动理论求解其动力响应．本文采用对数律风剖面模拟平均风速，采用沿高度变化的Kaimal风速谱[12-14]模拟输电塔结构的脉动风速．

1.3 风沙荷载计算

沙尘暴往往是伴随风荷载共同作用的．研究沙尘颗粒荷载对输电塔结构的影响，实际上是研究风荷载与沙粒荷载叠加后的荷载对输电铁塔的影响[11-12]．因此，本文将沙尘颗粒荷载计算模型与风荷载模型相叠加，则风沙荷载计算模型为

F=Fw+Fs

(11)

式中，F为单位体积内风沙荷载；Fw为单位体积内风荷载；Fs为单位体积内沙尘颗粒荷载．

塔身风荷载计算公式为

(12)

式中，μs为输电塔结构的体型系数；Vs(t)为风速．

由式(10)和(12)可得

(13)

2 数值模拟

2.1 算例

本文以某一双回路500 kV输变电工程中的ZSZH型塔[15](铁塔呼高54 m)为研究对象，并采用SAP2000有限元软件进行建模和数值分析．铁塔有限元模型如图1所示．ZSZH型输电角钢塔为双回路羊角直线塔，塔全高为84.3 m，正面半根开为8.625 m，最大主材规格为2×L200 mm×16 mm，全塔由Q345和Q235两种材质组成．ZSZH型塔的上横担长12.34 m，中横担长14.13 m，下横担长12.13 m．

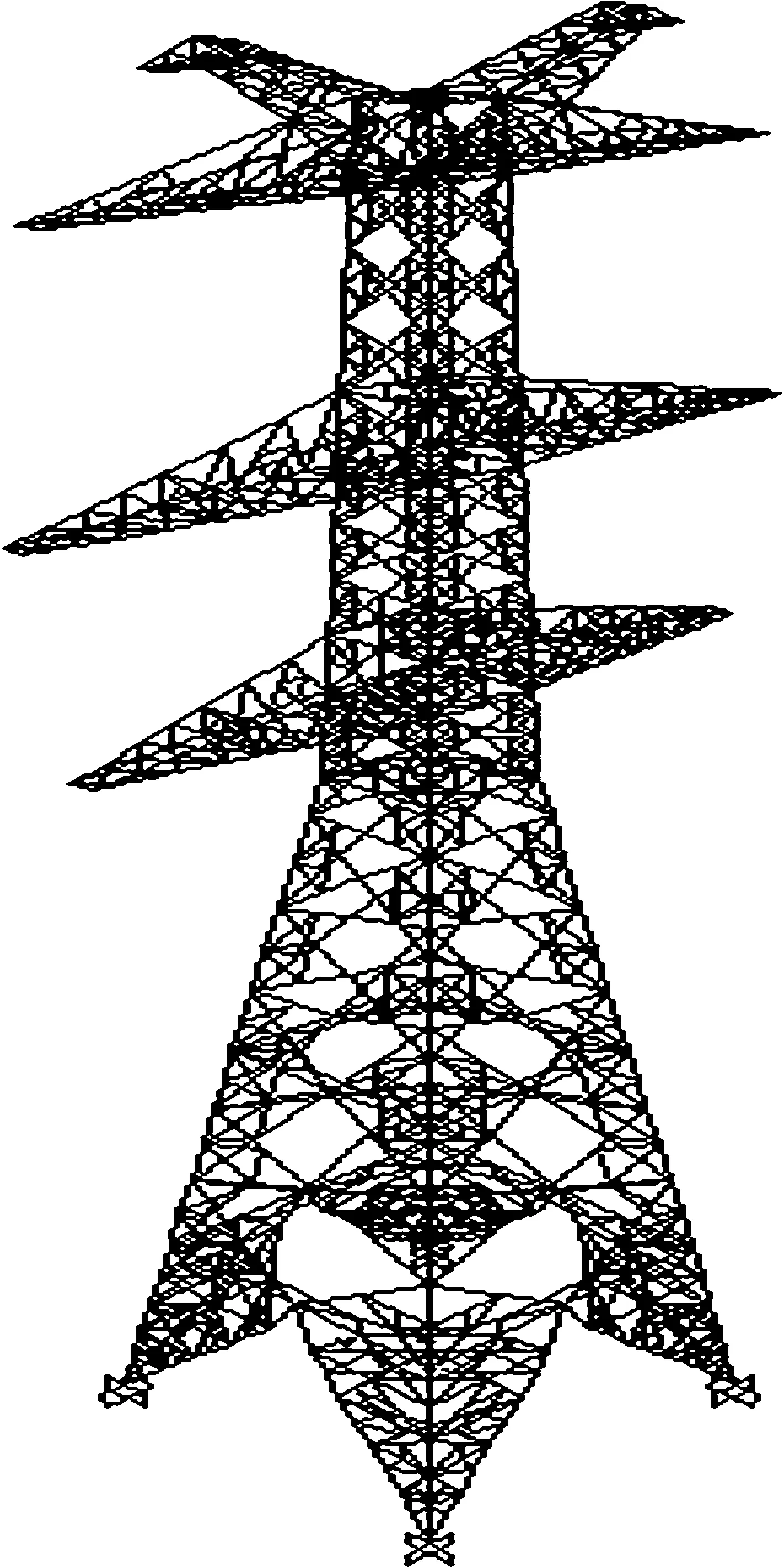
图1 输电塔有限元模型

2.2 风荷载模拟

为了方便计算，ZSZH型塔风荷载模拟点简化为21个点，具体模拟点位置高度与数值详见图2和表2．

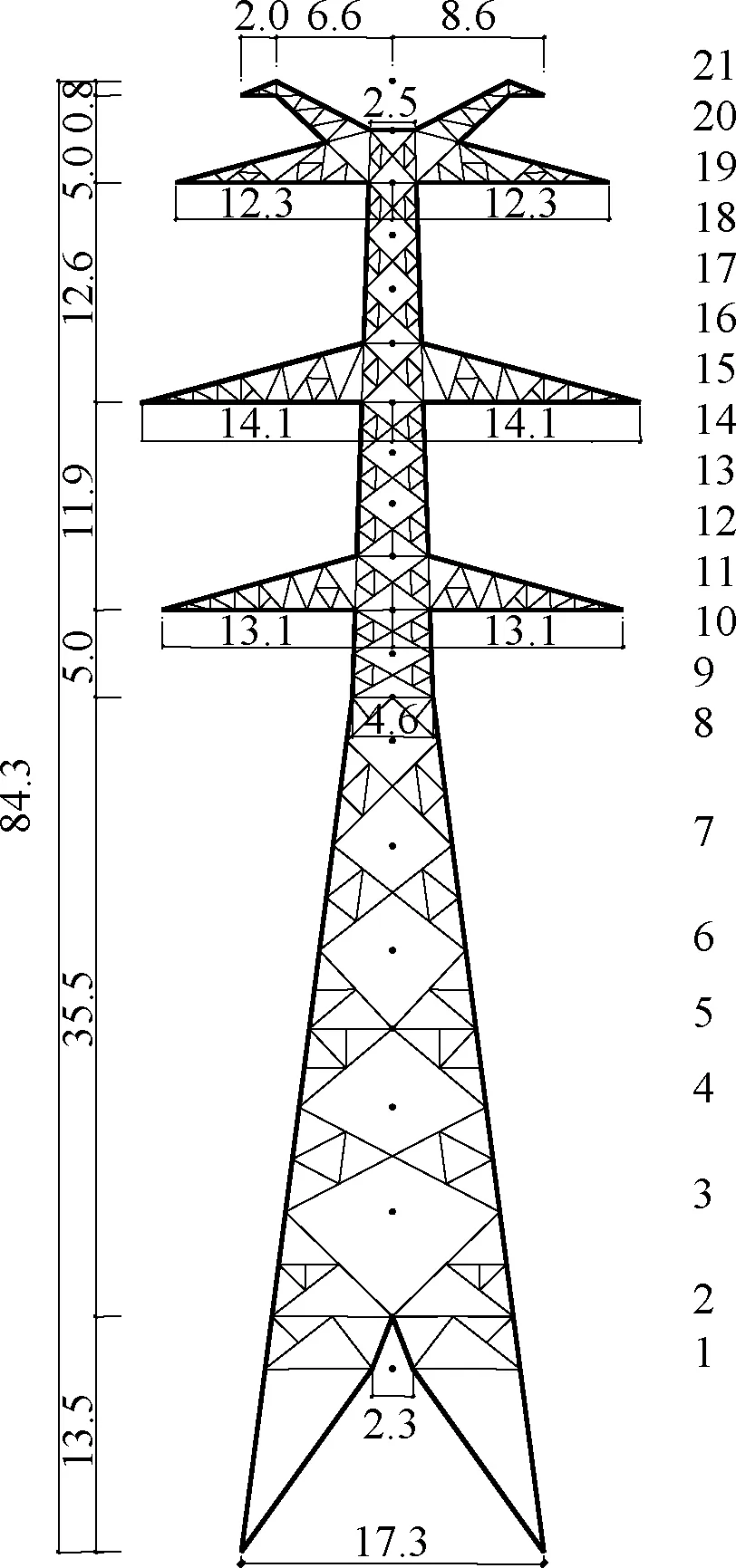
图2 模型风模拟代表点高度(单位：m)

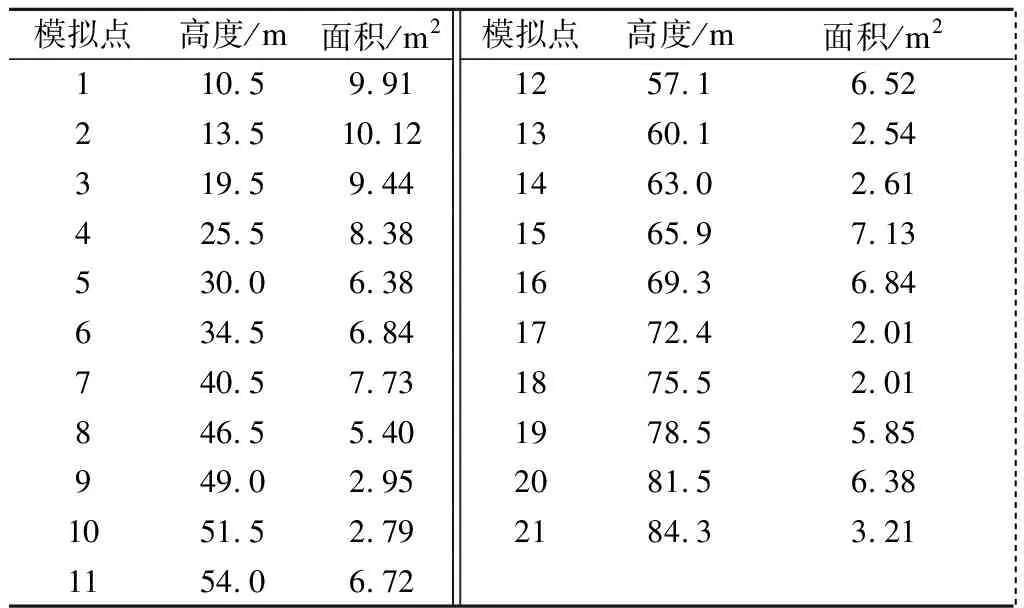
表2 风荷载模拟点高度

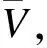
2.3 风沙荷载模拟

由式(13)可知，沙粒荷载计算方法与风荷载相一致，均与风速相关，且随高度变化而变化．由于输电塔为高耸结构，考虑到工程计算的安全性与误差要求，在实际应用中仅考虑沙粒的顺风向荷载，且vs取顺风向平均风速．基于式(13)，宽度设置为0.1，可得单位长度构件风沙荷载的顺风向时程曲线．

图5为仅考虑风荷载作用时输电塔模拟点14(高度63.0 m，强沙尘暴等级)的风荷载时程曲线．图6为考虑风沙荷载作用时输电塔模拟点14的风沙荷载时程曲线．

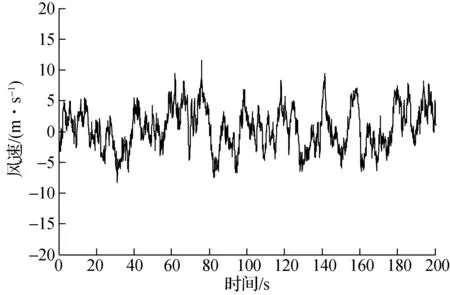
图3 模拟点10的脉动风速时程曲线

图4 模拟点10的脉动模拟功率谱与目标功率谱比较

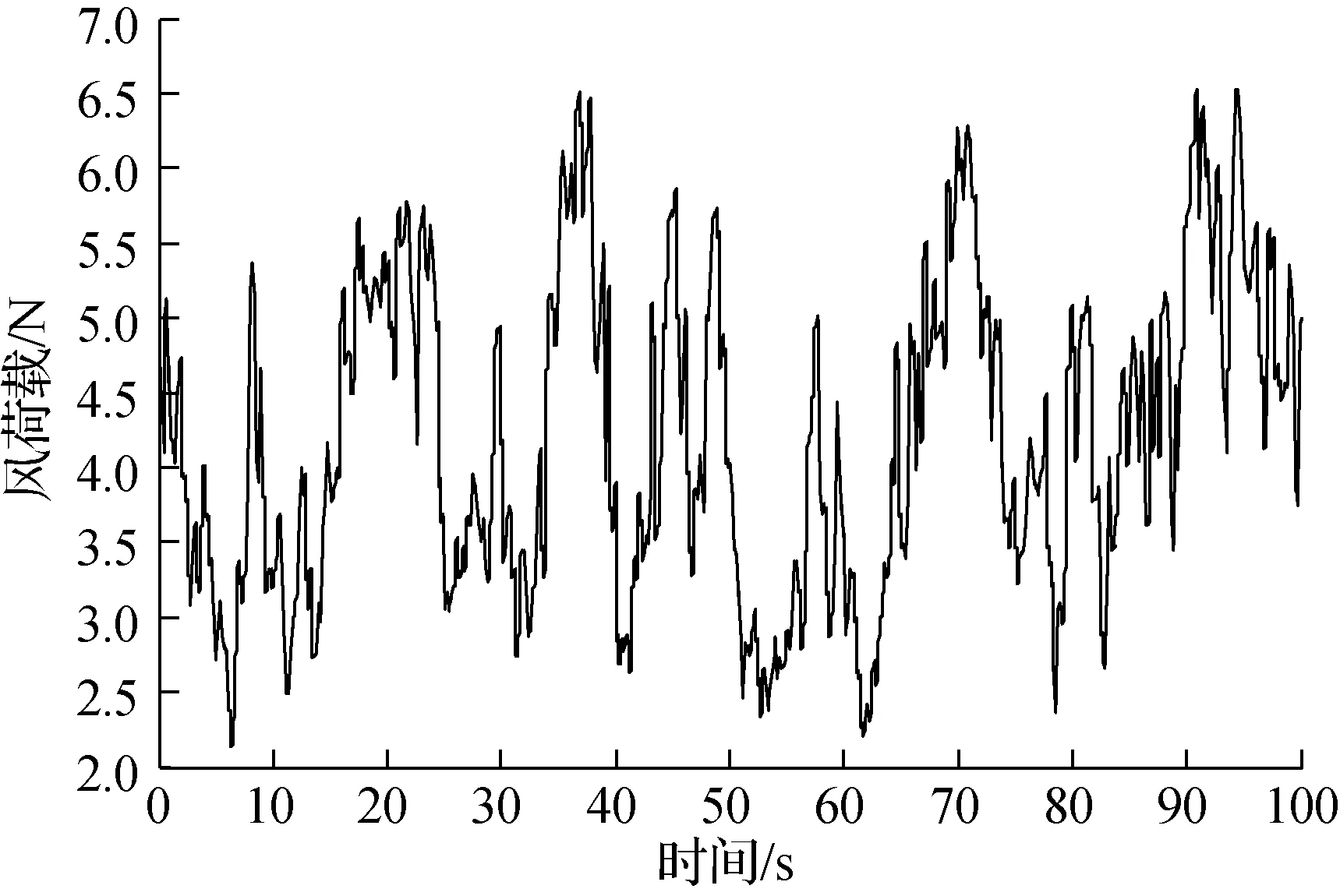
图5 模拟点14的风荷载时程曲线

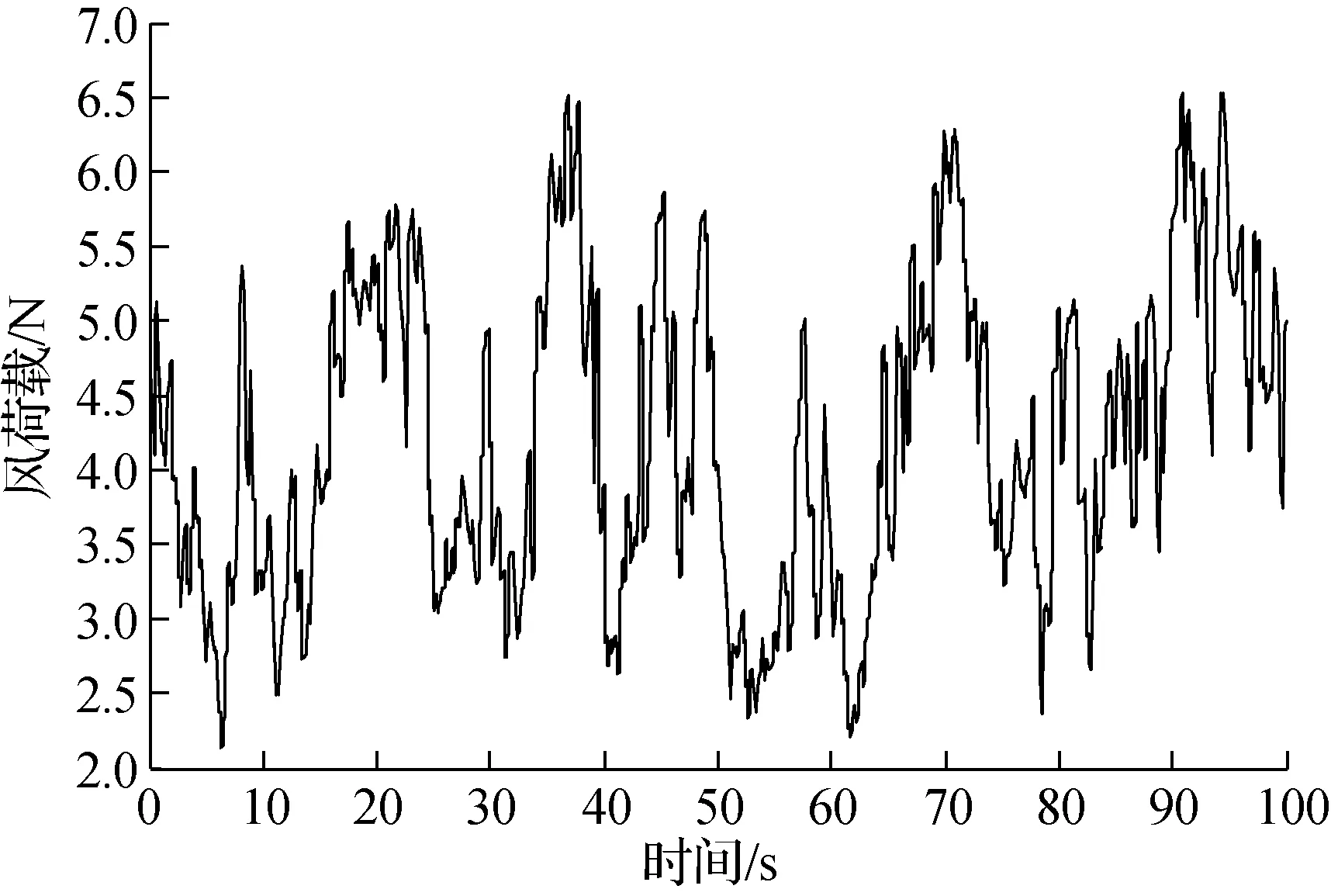
图6 模拟点14的风沙荷载时程曲线

2.4 结果分析

基于风速脉动时程与风沙荷载时程理论，利用有限元动力分析方法和SAP2000软件对输电塔分别进行了风荷载与风沙荷载的单塔激励动力响应分析．按照6种不同等级的风沙荷载，分别模拟了不同风速下的风荷载与风沙荷载．通过对不同等级风载单独激励与风沙荷载共同激励下结构的动力响应分析与对比，求解出输电塔结构在不同沙尘暴荷载等级下风荷载与风沙荷载对输电塔塔顶顺风向最大位移的影响，结果见表3．

表3 不同荷载作用下塔顶顺风向最大位移

由表3可知，考虑风沙激励时，在6种不同等级的沙尘暴情况下，ZSZH型塔的塔顶顺风向位移和动力响应均随风沙荷载等级的增大而增大．当风速为3 m/s时，风荷载单独作用下的塔顶最大顺风向位移为3.26 mm，而风沙荷载(浮尘)作用下的塔顶最大顺风向位移为3.31 mm，增加了1.56%．当风速为25 m/s时，风荷载单独作用下的输电塔塔顶最大顺风向位移为232.20 mm，而风沙荷载(特强沙尘暴)作用下的塔顶最大顺风向位移为317.82 mm，增加了26.94%，远高于之前的增长幅度．由此可知，随着风沙荷载等级的增大，输电塔塔顶位移增加幅度也逐渐加大．因此，多风沙灾害地区的输电塔结构应特别考虑风沙荷载的效应，且风沙灾害应该得到更广泛的关注和进一步研究．特别是发生极端风沙灾害时，输电塔很可能发生非常严重的破坏，进而导致巨大的经济损失．

3 结论

1) 本文基于动量守恒定律和风压计算公式，参考我国沙尘颗粒浓度参数，建立了风沙荷载力学计算模型，提出了可应用于输电杆塔结构设计的数值模拟方法．

2) 通过对比单独风荷载与风沙荷载作用下杆塔结构的动力响应特点发现，考虑风沙荷载激励的影响后，输电铁塔的动力响应和塔顶位移均随着风沙等级的增大而增大．

3) 虽然风荷载是输电塔结构的主要设计荷载，但是沙尘颗粒对输电塔的动力响应也具有明显的破坏效益，并随着沙尘暴等级的增大而逐渐增大．因此，在多风沙灾害的地区，风沙荷载对输电线路的危害应得到更多关注．

参考文献(References)

[1] Li Hongnan, Bai Haifeng. High-voltage transmission tower-line system subjected to disaster loads[J].ProgressinNaturalScience, 2006,16(9): 899-911. DOI:10.1080/10020070612330087.

[2] 张卓群, 李宏男, 李士锋, 等. 输电塔-线体系灾变分析与安全评估综述[J]. 土木工程学报, 2016,49(12): 75-88.

Zhang Zhuoqun, Li Hongnan, Li Shifeng, et al. Disaster analysis and tower-line safety assessment on transmission system：An overview[J].ChinaCivilEngineeringJournal,2016,49(12):75-88. (in Chinese)

[3] Bagnold RA.Thephysicsofwindsandanddesertdune[M]. New York：Willian Morrow & Co，1943: 265．

[4] Woodruff N P, Siddoway F H. A wind erosion equation[J].SoilScienceSocietyofAmericaProceedings, 1965,29(5): 602-608.DOI:10.2136/sssaj1965.03615995002900050035x.

[5] 李田.高速列车流固耦合计算方法及动力学性能研究[D]. 成都: 西南交通大学交通运输与物流学院, 2012.

[6] 中华人民共和国国家质量监督检查检疫总局. GB/T 20480—2006沙尘暴天气等级[S]. 北京: 中国标准出版社, 2006.

[7] 严颖, 狄少丞, 苏勇, 等. 风沙影响下铁路道碴变形模量的离散元数值分析[J].计算力学学报, 2012,29(3):439-445.

Yan Ying, Di Shaocheng, Su Yong, et al. Discrete element analysis of elastic modulus of railway ballasts in wind with different sand contents[J].ChineseJournalofComputationalMechanics, 2012,29(3): 439-445. (in Chinese)

[8] 程建军, 蒋富强, 薛春晓, 等. 强风区铁路风沙防治工程最大输沙量与携沙风荷载计算方法[J]. 中国铁道科学,2012,33(1):1-5. DOI: 10.3969/j.issn.1001-4632.2012.01.01.

Cheng Jianjun, Jiang Fuqiang, Xue Chunxiao, et al. Computational method for maximum sediment discharge and sand-carrying wind load in the prevention and treatment of wind drift sand for railway in strong wind area[J].ChinaRailwayScience, 2012,33(1): 1-5. DOI: 10.3969/j.issn.1001-4632.2012.01.01.(in Chinese)

[9] 郝贠洪,邢永明,冯玉江,等.钢结构表面涂层材料抗风沙冲蚀力学性能研究[J]. 建筑材料学报, 2013,16(6): 1092-1096. DOI:10.3969/j.issn.1007-9629.2013.06.031.

Hao Yunhong, Xing Yongming, Feng Yujiang, et al. Research on anti-erosion mechanical properties of steel structure coating[J].JournalofBuildingMaterial, 2013,16(6): 1092-1096. DOI:10.3969/j.issn.1007-9629.2013.06.031. (in Chinese)

[10] 李宏男, 任月明, 白海峰. 输电塔体系风雨激励的动力分析模型[J]. 中国电机工程学报, 2007,27(30):43-48. DOI: 10.3321/j.issn:0258-8013.2007.30.008.

Li Hongnan, Ren Yueming, Bai Haifeng. Rain-wind-induced dynamic model for transmission tower system[J].ProceedingsoftheCSEE,2007,27(30)：43-48. DOI: 10.3321/j.issn:0258-8013.2007.30.008. (in Chinese)

[11] Zhang Z, Li H, Li G, et al. The numerical analysis of transmission tower-line system wind-induced collapsed performance[J].MathematicalProblemsinEngineering, 2013,2013: 1-11. DOI:10.1155/2013/413275.

[12] Simiu E, Scanlan R.H.Windeffectsonstructures[M]. 3rd ed. New York:John Wiley & Sons Inc, 1996: 33-82.

[13] Shinozuka M, Jan C M. Digital simulation of random processes and its applications[J].JournalofSoundandVibration, 1972,25(1): 111-128. DOI:10.1016/0022-460x(72)90600-1.

[14] 张相庭. 工程结构风荷载理论和抗风计算手册[M].上海: 同济大学出版社, 1990:226-239.

[15] 张卓群, 李宏男, 李东升, 等. 高压输电塔结构的疲劳寿命分析[J]. 电力建设, 2014,35(1): 14-18. DOI:10.3969/j.issn.1000-7229.2014.01.003.

Zhang Zhuoqun, Li Hongnan, Li Dongsheng, et al. Fatigue life analysis of HV transmission tower structure[J].ElectricPowerConstruction, 2014,35(1): 14-18.DOI:10.3969/j.issn.1000-7229.2014.01.003. (in Chinese)