基于等电势梯度模型试验的滩涂淤泥电渗效率分析

郑凌逶 谢新宇 谢康和 臧俊超 李卓明

(1浙江大学滨海和城市岩土工程研究中心, 杭州 310058)(2浙江大学宁波理工学院, 宁波 315100)

电渗现象最早由俄罗斯科学家Reuss发现,自1939年Casagrande[1]将电渗应用于地基处理之后,土的电渗理论及工程应用不断得到丰富.电渗法加固软土地基的机理是在土中插入电极,直流电场作用下土体中的水分随阳离子流向阴极并排出,提高软土地基的抗剪强度和黏聚力[2].不同土的电渗透系数差别不大,细颗粒土的电渗流速相对水力流速高出2～4个数量级[3],电渗法更适用于处理高塑性、低渗透性的细颗粒土.

Esrig[4]在电渗流-水力流可叠加假设前提下,推导了一维电渗固结理论及其解析解.在此基础上,Wan等[2]研究了电极反转技术在理论上的有效性.Wu等[5]考虑电渗透系数、水力渗透系数、电导率、压缩系数的非线性变化,对电渗固结过程进行了多场耦合数值模拟.Xue等[6]进行了铁电极和铜电极的电渗加固试验,结果表明主要电势损失发生在阳极-土界面,铁电极的电渗排水效果相对更好.Glendinning等[7]采用导电高分子材料研制电动土工合成材料(electro-kinetic geosynthetics,EKG),减少了电极腐蚀对电渗的负面影响,但其界面电阻相对金属更高.间歇通电[8]和逐级加压[9]等工艺研究结果表明,需要合理设计才能提升排水效果、降低电能消耗.

电渗法处理地基所采用的电压范围和电势梯度范围较广,不同工况下的能耗差别甚至可达2个数量级[10].本文根据相似原理进行等电势梯度条件下的电渗模型试验,获得排水量、通电电流、电势等试验数据,研究了电渗能耗、电势利用率与电极间距的关系,并对不同工况下的电势利用率和能耗系数进行了讨论.

1 模型试验设计

1.1 模型试验相似关系

土体电渗排水加固过程中的主要因素包括：土体特征尺寸Ls、电极间距Le、外加电势梯度G、土的电导率σe、电渗透系数ke、水力渗透系数kh、含水率w、泊松比ν、孔隙比e、相对密度Gs、排水量Qe、排水速率qe、电渗流速ve、通电电流I、能耗系数Ce和处理时间t.采用与原型相同的软土是容易且能做到的[11],忽略重力影响,在外加电势梯度的作用下,以Ls,G,σe,ke为基本量进行量纲分析,根据Π定理[12]可得

(1)

本次试验中,模型和原型的几何相似比为1∶4.G,σe,ke与原型情况相同,模型与原型各物理量的相似比关系见表1.

表1 模型试验物理量的相似比

1.2 试验方案

采用改进的米勒盒(Miller soil box)[13]进行7组电渗试验,模型试验箱的横截面尺寸均为130 mm×120 mm.设置不同的电极间距Le,对应不同的外加电压U,以保证各组试验的外加电势梯度G=U/Le=0.625 V/cm.阴阳电极均采用铜电极板,尺寸为130 mm×120 mm×4 mm,阴极板打孔处理并设置排水槽收集、测量电渗排水.电势测针N1和N2分别距离阴阳极1 cm,电势测针间距为x并随试验箱尺寸而变化,模型试验箱如图1所示.试验用土为取自浙江宁海的滩涂淤泥,原状土的基本物理力学性质指标见表2.

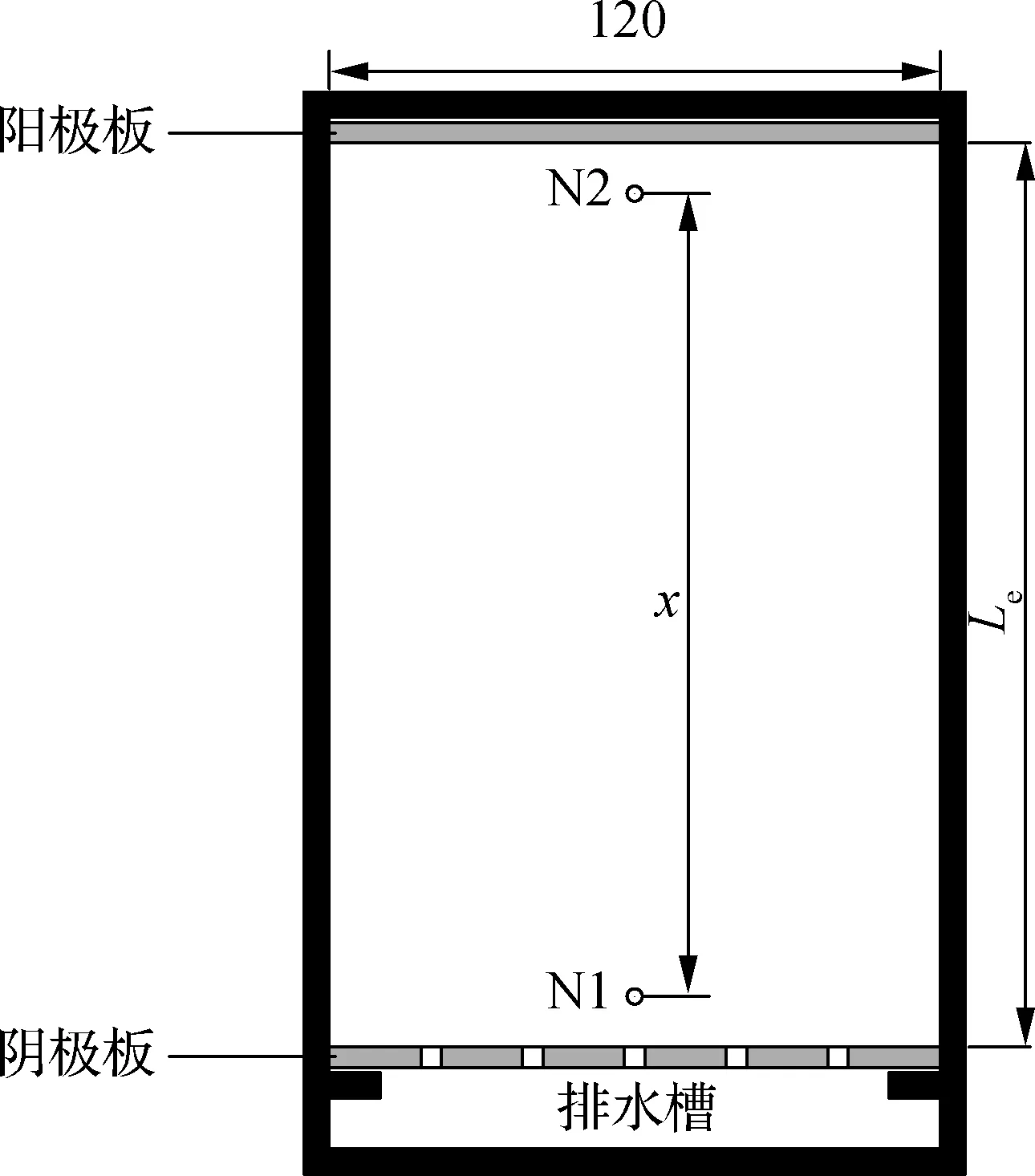
图1 模型试验箱俯视图(单位:mm)

表2 原状土的物理力学性质指标

试验前将原状土烘干、粉碎并加水搅拌调制成重塑土样.将重塑土样以分层填筑的方式装入试验箱,填土高度距离顶面1 cm.通电前土样在模型试验箱内静置12 h.试验过程中每隔1 h采集一次排水量、通电电流和电势数据,43 h后结束通电.各组试验电势测针N1和N2的间距x及初始含水率wini见表3.

表3 等电势梯度试验方案

2 试验结果

2.1 排水量

电渗试验排水量随时间变化曲线见图2.由图可知,随着电极间距的缩短,T1～T7最终排水量呈下降趋势.在0～10 h时间段(电渗前期阶段),排水量与时间基本呈线性关系,排水速率稳定,土体几何尺寸和完整性变化不大,适合进行规律分析.

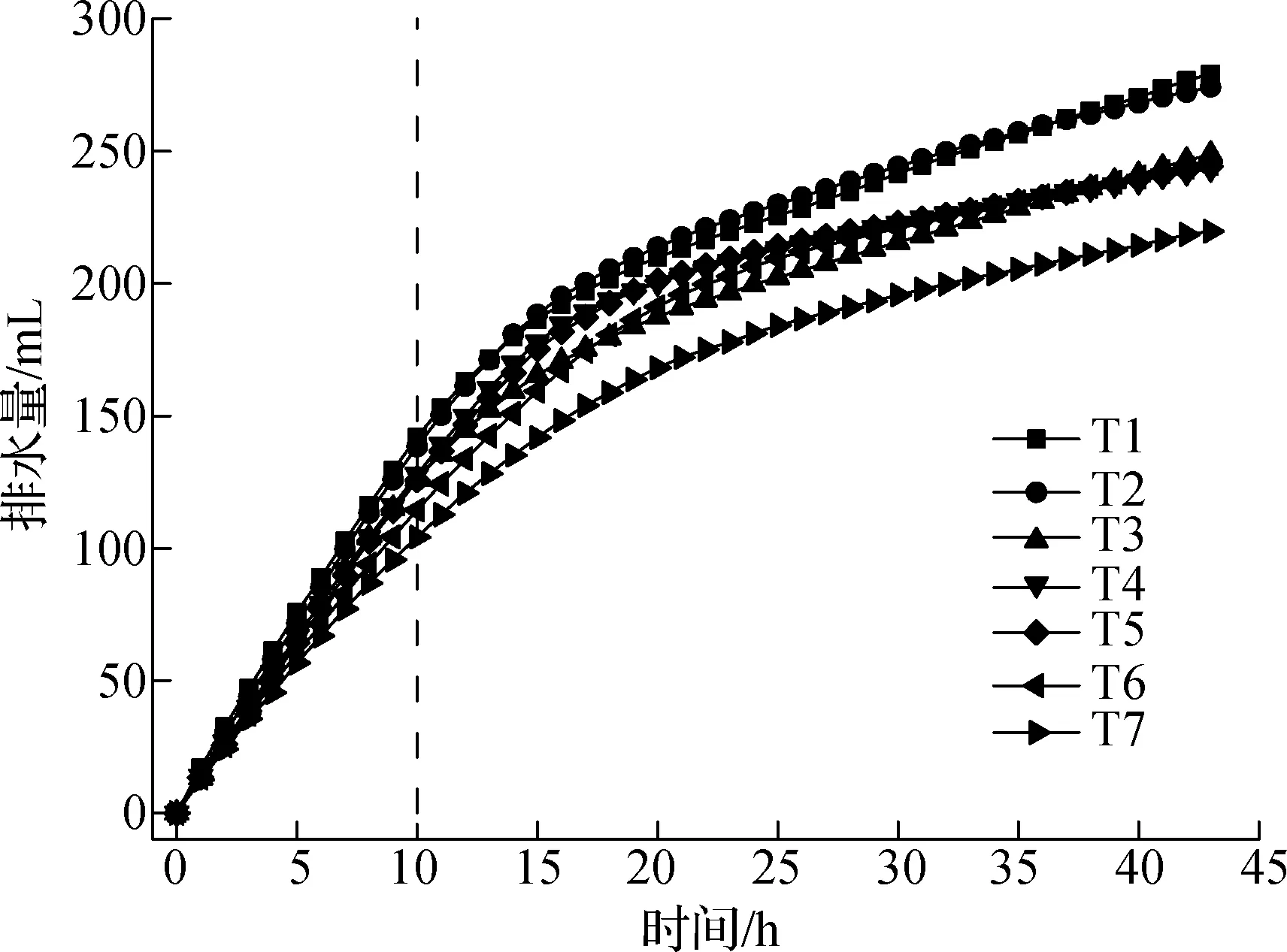
图2 电渗排水量与时间的关系曲线

2.2 通电电流

图3显示通电电流在电渗过程中随时间下降,在0～10 h时间段(电渗前期阶段)内电流曲线规律性较好.7组试验电流曲线在电渗前期阶段区分较为明显,电极间距越小,电流值越低.10～25 h时间段(电渗中期阶段)内,7组试验电流曲线开始出现交叉.前期阶段电流值高的试验组排水速率高、后期衰减快,前期阶段电流值低的试验组排水速率低、后期衰减慢.

图3 通电电流与时间的关系曲线

2.3 有效电势梯度

电极-土界面存在界面电阻Rir,土体在电渗过程中的有效电压小于外加电压,影响外加电压U的利用率.考虑界面电阻产生的电势损失,采用有效电势原理对有效电势进行表述,即

U′=U-Uir

(2)

式中,U′为有效电势,V；U为外加电压,V；Uir为界面电阻Rir产生的电势损失,V.

电势测针N1和N2分别距离阴极和阳极1 cm,两者之间的电势差与土体电渗的有效电势接近,并可换算成有效电势梯度.有效电势梯度随时间变化曲线如图4所示.

图4 有效电势梯度与时间的关系曲线

由图4可知,在电渗前期阶段,有效电势梯度保持相对稳定,T1～T7呈递减趋势.在电渗中期阶段后,存在有效电势梯度快速下降的区间.在此区间内,界面电阻值增速超过中部土体电阻值增速,使中部土体电阻占总电阻的比例降低,有效电势及有效电势梯度快速下降.

2.4 能耗系数

试验采用的直流电源为恒压输出,通过试验过程中的电渗排水、通电电流数据可计算各组试验的能耗系数Ce，即

(3)

式中,Qi为时刻i的累计排水量,mL；Ii为时刻i的电流,A；能耗系数Ce用于表征排出1 mL水所消耗的电能,W·h/mL.

电渗过程中能耗系数随时间的变化规律如图5所示.由图可知,随着T1～T7电极间距的缩短,电渗能耗系数呈递减趋势,在电渗前期阶段区分更为明显.在电渗前期阶段(0～10 h),T7的能耗系数均值为0.54 W·h/mL,仅为T1的1/2左右.

图5 能耗系数与时间的关系曲线

各组试验在电渗前期阶段(0～10 h)的能耗系数实测值(均值)与拟合曲线见图6.由图可知,能耗系数与电极间距呈线性关系,拟合式为

Ce=0.042Le

(4)

图6 能耗系数实测值与拟合曲线

3 有效电势原理分析

3.1 原理和假定

根据电渗排水理论,稳定阶段的电渗排水速率[1]为

(5)

式中,E为施加在阴极和阳极之间的电势差,V；S为土体的横截面面积,cm2.

现实中电极-土界面存在界面电阻,根据有效电势原理,相同的外加电势梯度G下,不同的电极间距对应不同的有效电势梯度G′.基本假定如下：① 忽略电渗过程中电化学作用、产气、浓度差和热差对土体造成的影响；② 电渗过程中土体保持均匀,形状、组成成分和电学特性不发生变化；③ 电极间距、外加电压的变化均基于外加电势梯度G不变的前提；④ 平行于土体横截面每1 cm厚的单位土层电阻值为RL,各组试验箱电极-土的界面电阻Rir相等且保持不变.

在电渗中后期,电极腐蚀、土体开裂变形情况存在差异,各组试验的土体状况差别增大,土体电阻和界面电阻发展不均衡；而电渗前期阶段(0～10 h)土体较为均匀,各组试验之间的差别较小,更符合所提出的基本假定,因此采用该时间段的数据进行分析.

3.2 能耗分析

将7组模型试验前期阶段(0～10 h)电渗排水速率均值和有效电势梯度均值进行拟合,两者呈线性关系(见图7).

图7 电渗排水速率实测值与拟合曲线

电渗排水速率和有效电势梯度的关系式为

qe=αG′

(6)

式中,α=keS,其拟合值为29 cm4/(V·h).

土体电阻Rs=RLLe,外加电压U=GLe,结合假定④和有效电势原理,通电电流可表示为

(7)

式中,RL为平行于土体横截面每1 cm厚度的单位土层电阻值,Ω/cm.

根据7组电渗试验前期阶段的平均通电电流数据,可以确定RL=0.540 Ω/cm,Rir=3.250 Ω.根据式(2)可知

(8)

在满足假定④和式(6)的前提下,电渗排水速率与有效电势梯度呈正比关系,即电渗排水速率和通电电流呈正比关系.当G,RL,Rir为定值时,式(7)和(8)可绘制成双纵坐标的重合曲线(见图8).电势测针N1和N2距离阴、阳极尚有1 cm,通电电流换算的有效电势梯度曲线偏高于实测值.

图8 通电电流、有效电势梯度实测值与拟合曲线

根据假定④和式(7)可以得到以电极间距Le为变量的功率P表达式为

(9)

结合式(6)和(8)可知,以电极间距Le为变量的排水速率为

(10)

结合式(9)和(10),可以得到以电极间距Le表示的能耗系数为

(11)

等电势梯度、不同电极间距情况下,土体降低相同的含水率w′需达到的排水量为

(12)

结合式(10)可得所需处理时间为

(13)

式中,γd为土的干重度,kN/m3；γw为水的重度,kN/m3.

以电极间距Le表示的能耗系数曲线和处理时间曲线(w′=5%)如图9所示.结合式(11)和(13)可知,等电势梯度下,随着电极间距的缩短,能耗系数线性下降,达到相同处理效果所需时间更短.

图9 能耗系数和处理时间计算曲线

3.3 电势利用率和能耗系数分析

电势利用率为电渗过程中有效电势与外加电势的比值.等电势梯度下,以电极间距Le为变量的电势利用率η为

(14)

由式(6)、(8)和(14)可得，由电势利用率表示的电渗排水速率为

qe=αGη

(15)

采用新型电动土工合成材料(如EKG电极)会使界面电阻较高.在等电势梯度条件下,结合式(11)和(14),讨论界面电阻对电势利用率和能耗系数的影响.下面选取如下2种工况：① 与本试验工况相同,RL=0.540 Ω/cm,Rir=3.250 Ω；② 土体电阻与本次试验工况相同,界面电阻为本次试验工况的5倍.

2种工况下电势利用率、能耗系数与电极间距的关系曲线如图10所示.

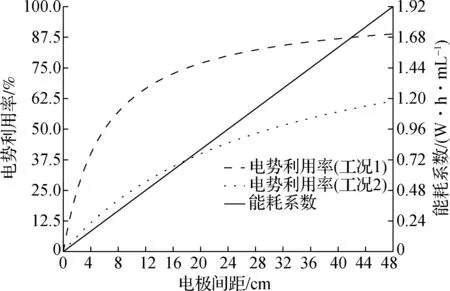
图10 电势利用率、能耗系数与电极间距的关系曲线

由图10可知,等电势梯度下,随着电极间距的扩大,电渗能耗系数Ce线性增加,电势利用率η增加但增速减缓.界面电阻越高,产生的表观电势损失越大,电势利用率越低，电渗排水速率越低,但不影响电渗能耗系数.

4 结论

1) 由于界面电阻的存在,等电势梯度下不同的电极间距对应不同的有效电势梯度,电渗排水速率和有效电势梯度呈线性关系.

2) 等电势梯度下,电渗能耗系数和电极间距呈线性关系.随着电极间距的缩短,能耗系数随之下降,达到相同处理效果所需的时间也越短.

3) 等电势梯度下,随着电极间距的扩大,电势利用率提高,但能耗系数增加.界面电阻越高,产生的表观电势损失越大，电势利用率越低,电渗排水速率越低,但不影响电渗能耗系数.

4) 建议在工程应用中尽量缩短电极间距,以降低电渗能耗、缩短工期.高界面电阻的新材料不影响电渗的能耗系数,仅影响电渗排水速率.选取合适的电极材料并采用合理的电极布置形式,能够提高电渗加固软土的效率和工程经济性.

参考文献(References)

[1] Casagrande I L. Electro-osmosis in soils[J].Géotechnique, 1949,1(3): 159-177. DOI: 10.1680/geot.1949.1.3.159.

[2] Wan T Y, Mitchell J K. Electro-osmotic consolidation of soils[J].JournaloftheGeotechnicalEngineeringDivision, 1976,102(5): 473-491.

[3] Jones C J F P, Lamont-Black J,Glendinning S. Electrokinetic geosynthetics in hydraulic applications[J].GeotextilesandGeomembranes, 2011,29(4): 381-390. DOI: 10.1016/j.geotexmem.2010.11.011.

[4] Esrig M I. Pore pressures, consolidation, and electrokinetics[J].JournaloftheSoilMechanicsandFoundationsDivision, 1968,94(4): 899-922.

[5] Wu H,Hu L, Wen Q. Numerical simulation of electro-osmotic consolidation coupling non-linear variation of soil parameters[J].Computers&Geosciences, 2017,103: 92-98. DOI: 10.1016/j.cageo.2017.03.002.

[6] Xue Z, Tang X, Yang Q, et al. Comparison of electro-osmosis experiments on marine sludge with different electrode materials[J].DryingTechnology, 2015,33(8): 986-995. DOI: 10.1080/07373937.2015.1011274.

[7] Glendinning S, Lamont-Black J, Jones C J F P. Treatment of sewage sludge using electrokinetic geosynthetics[J].JournalofHazardousMaterials, 2007,139(3): 491-499. DOI: 10.1016/j.jhazmat.2006.02.046.

[8] 陶燕丽, 周建, 龚晓南, 等. 间歇通电模式影响电渗效果的试验[J]. 哈尔滨工业大学学报, 2014, 46(8): 78-83. DOI: 10.11918/j.issn.0367-6234.2014.08.013.

Tao Yanli, Zhou Jian, Gong Xiaonan, et al. Experimental research of the influence of current intermittence on electro-osmotic effect[J].JournalofHarbinInstituteofTechnology, 2014,46(8): 78-83. DOI: 10.11918/j.issn.0367-6234.2014.08.013. (in Chinese)

[9] 刘飞禹, 宓炜, 王军, 等. 逐级加载电压对电渗加固吹填土的影响[J]. 岩石力学与工程学报, 2014, 33(12): 2582-2591. DOI: 10.13722/j.cnki.jrme.2014.12.025.

Liu Feiyu, Mi Wei, Wang Jun, et al. Influence of applying stepped voltage in electroosmotic reinforcement of dredger fill[J].ChineseJournalofRockMechanicsandEngineering, 2014,33(12): 2582-2591. DOI: 10.13722/j.cnki.jrme.2014.12.025. (in Chinese)

[10] Malekzadeh M, Lovisa J, Sivakugan N. An overview of electrokinetic consolidation of soils[J].GeotechnicalandGeologicalEngineering, 2016,34(3): 759-776. DOI:10.1007/s10706-016-0002-1.

[11] 张智超, 陈育民. 微型桩-加筋土挡墙路基结构的模型试验研究[J]. 东南大学学报(自然科学版), 2016, 46(S1): 217-224. DOI: 10.3969/j.issn.1001-0505.2016.S1.038.

Zhang Zhichao, Chen Yumin. Model test study on micropile-MSE wall for subgrade[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016,46(S1): 217-224. DOI: 10.3969/j.issn.1001-0505.2016.S1.038. (in Chinese)

[12] 谈庆明. 量纲分析[M]. 合肥:中国科学技术大学出版社, 2005: 12-18.

[13] 储亚, 刘松玉, 蔡国军, 等. 重金属污染黏性土电阻率影响因素分析及其预测模型[J]. 东南大学学报(自然科学版), 2016, 46(4): 866-871. DOI: 10.3969/j.issn.1001-0505.2016.04.032.

Chu Ya, Liu Songyu, Cai Guojun, et al. Impact factor analysis of resistivity of heavy metal polluted cohesive soil and its prediction model[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016,46(4): 866-871. DOI: 10.3969/j.issn.1001-0505.2016.04.032. (in Chinese)