有垫片铺浆砌筑足尺粗料石砌体墙体抗震性能试验研究

高晓鹏 陈忠范

(东南大学土木工程学院， 南京 210096)(东南大学混凝土及预应力混凝土结构教育部重点实验室， 南京 210096)

我国福建沿海村镇地区存在大量的石砌体古建筑和村镇石砌体建筑(如崇武墙和开元寺东西塔等)．在地震作用下，这些石墙体作为最基本的侧向承载力构件起着重要的作用．然而，这些石砌体古建筑和村镇建筑大部分是基于经验设计的，存在安全系数缺乏和尺寸控制不合理等缺点．

目前，砌体研究主要针对黏土砖和混凝土砌块，关于石砌墙体的研究则相对较少．郭子雄等[1-2]针对墙体尺寸为2 400 mm×1 200 mm×200 mm(长×高×厚)的缩尺干砌甩浆石墙和机器切割的缩尺石墙进行了抗震性能研究，分析了砂浆强度、竖向压应力、灰缝界面处理方式和灰缝水平配筋对墙体抗震性能的影响；徐天航等[3]利用钢筋网片改进砂浆加固尺寸为2 370 mm×1 410 mm×200 mm(长×高×厚)的缩尺干砌石墙，发现这种加固方法能有效提高墙体抗剪承载力；郭子雄等[4]采用嵌缝加固方法对2 370 mm×1 180 mm×200 mm(长×高×厚)的缩尺干砌甩浆墙体进行加固，嵌缝加固后墙体的抗震能力明显改善；Vasconcelos等[5]采用1∶3缩尺单页机器切割石砌墙体研究了块体布置形式对石砌墙体的抗震性能影响；Silva等[6]采用2∶3缩尺的三页石砌体墙体进行了低周反复试验．然而，关于足尺石砌墙体的低周反复试验研究和石墙体的抗震性能评估较少见报道．

本文通过对6片足尺有垫片粗料石墙体进行低周反复加载试验，研究分析了竖向压应力、砂浆强度和石块尺寸对石墙抗震性能的影响，并利用已有文献中的简化公式预测粗料石砌体的抗剪承载能力．

1 试验

1.1 墙体施工步骤

墙体的施工步骤为：① 放置下层石块；② 砌筑砂浆并放置上层石块；③ 插入垫片并抹平砂浆．

1.2 墙体设计

墙体为单层单跨足尺石墙体，尺寸为4 250 mm×3 200 mm×250 mm(长×高×厚)，高宽比为0.81．墙体所用石材为泉州白花岗岩．6片墙体的参数设置见表1．

1.3 加载制度

试验的加载装置见图1．水平荷载通过MTS电液伺服系统施加于钢筋混凝土加载梁．竖向压应力由2个液压千斤顶及质量块施加，压力由分配钢梁经二次分配传递至钢筋混凝土加载梁，压力近似均匀分布在混凝土加载梁上，同时通过4根刚性螺杆传递水平荷载至墙体．

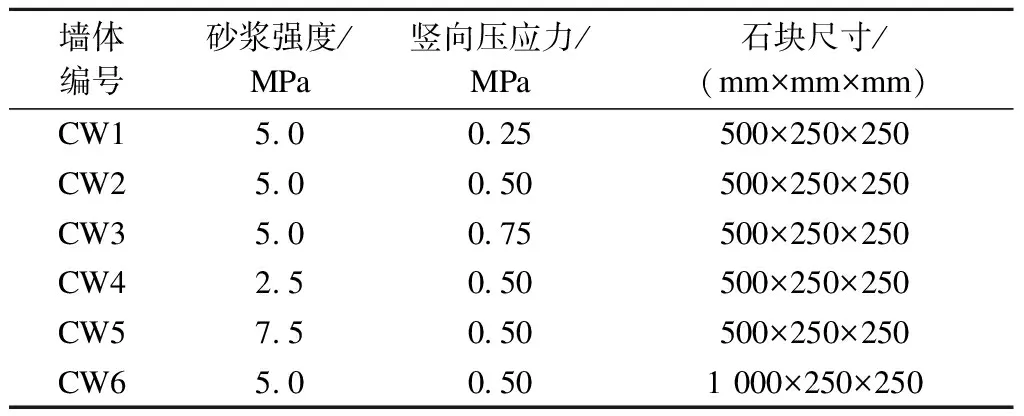
表1 墙体参数

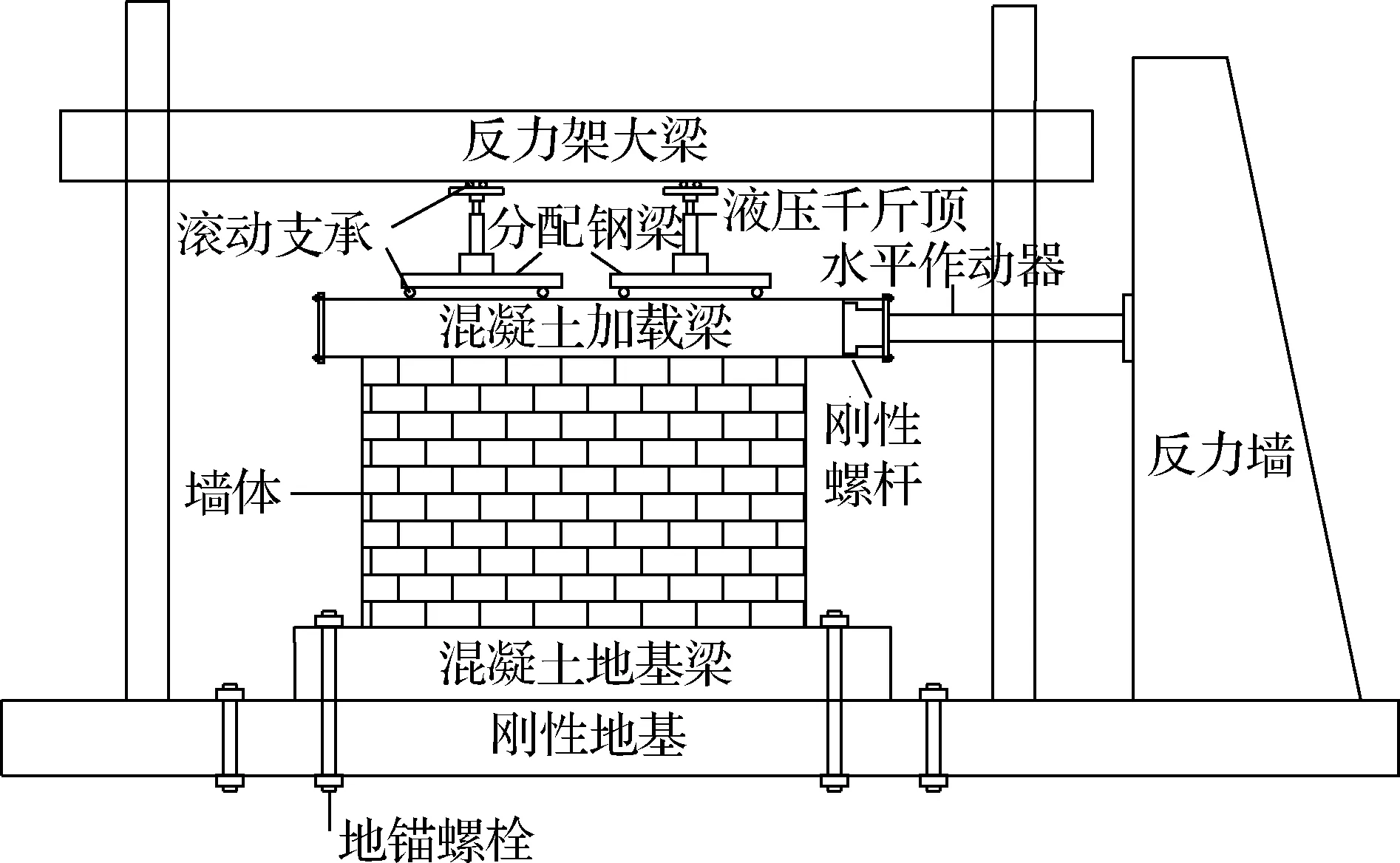
图1加载装置

加载制度采用力位移混合加载方式(见图2)．墙体开裂前采用力控制，荷载增量为50 kN，每级荷载循环一次，墙体出现斜裂缝后采用位移控制．试验数据由作动器上的拉压传感器和MTS液压伺服控制器采集．

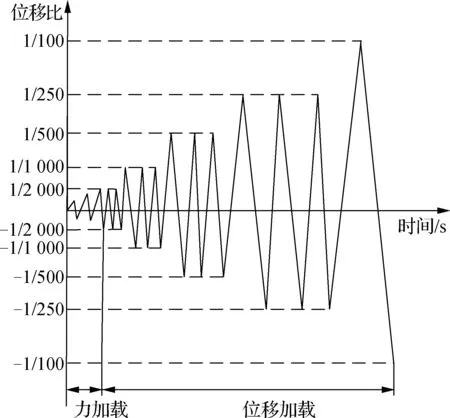
图2 加载制度

2 试验结果与分析

2.1 失效模型及墙体滞回曲线

图3显示了推力方向和拉力方向的最终开裂特征，裂缝草图则综合了推力和拉力方向的裂缝特征．墙体的力-位移滞回曲线见图4．由图可知，加载后期墙体承载力几乎保持不变或仅有较小的下降，究其原因在于，加载过程中砂浆失去黏结力，墙体的抗剪强度主要由砂浆界面的摩擦力承担，而砂浆界面摩擦力由石块界面的粗糙度和含有石垫片的砂浆提供，即砂浆界面能提供较高的摩擦耗能能力．

(a) CW1推方向失效模型

(b) CW1拉方向失效模型

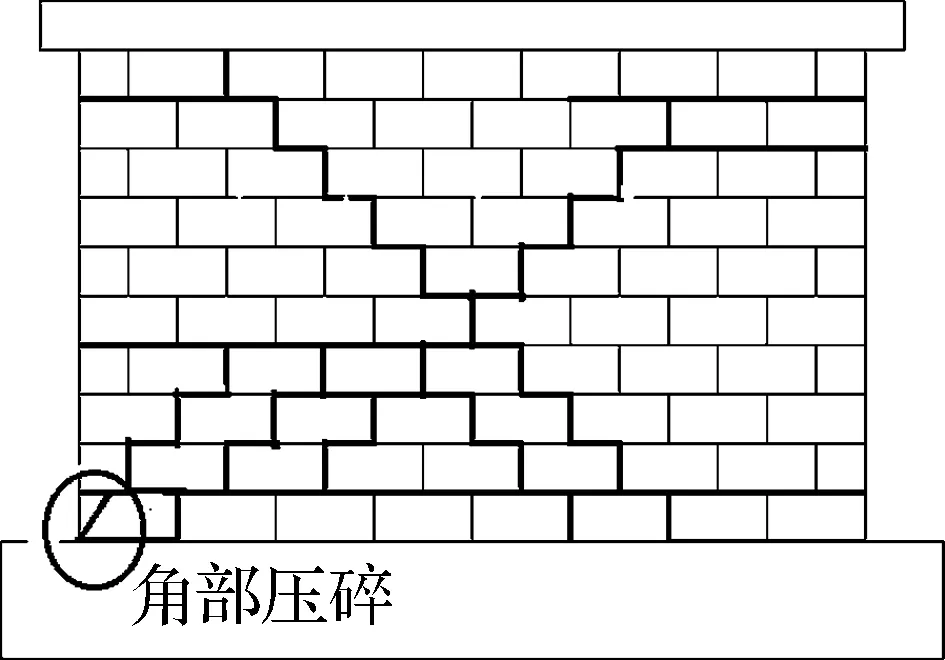
(c) CW1裂缝草图

(d) CW2推方向失效模型

(e) CW2拉方向失效模型

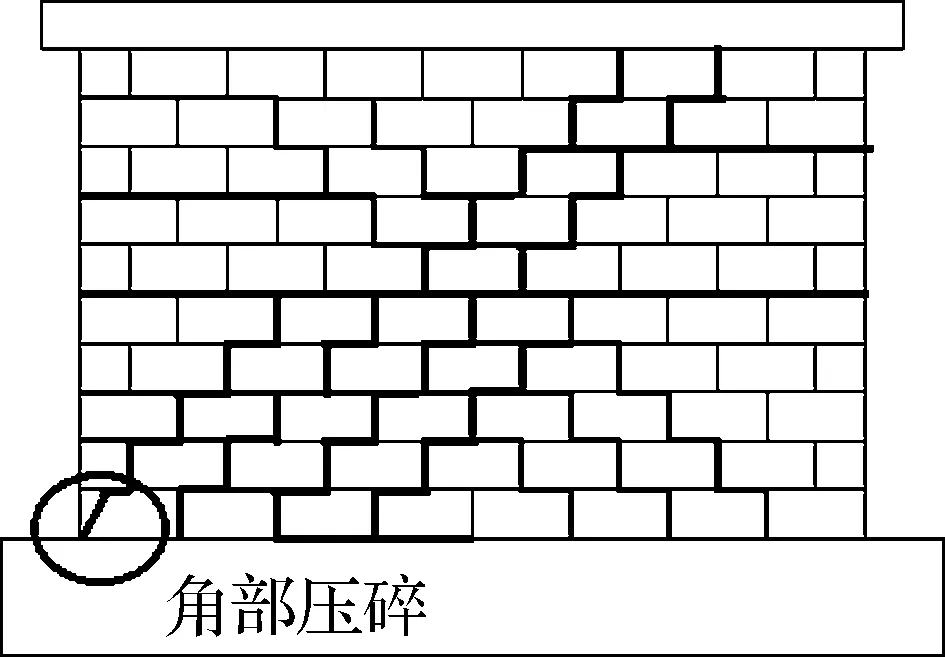
(f) CW2裂缝草图

(g) CW3推方向失效模型

(h) CW3拉方向失效模型

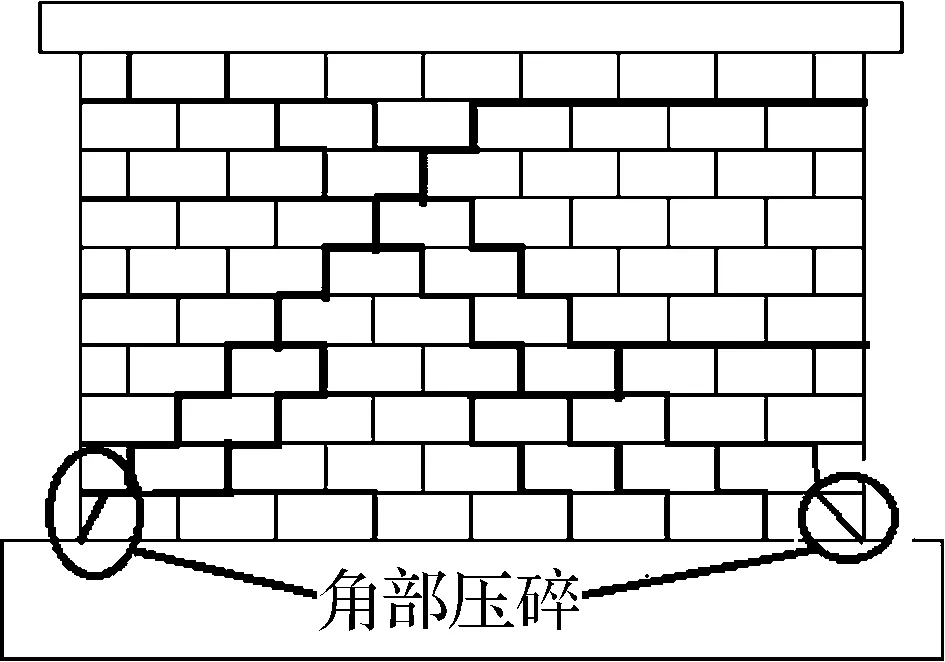
(i) CW3裂缝草图

(j) CW4推方向失效模型

(k) CW4拉方向失效模型

(l) CW4裂缝草图

(m) CW5推方向失效模型

(n) CW5拉方向失效模型

(o) CW5裂缝草图

(p) CW6推方向失效模型

(q) CW6拉方向失效模型

(r) CW6裂缝草图

图3墙体失效模型

墙体CW1～CW3的失效模型均为弯剪和角部石块压碎的失效模型．对于墙体CW1，在加载初期，墙体底部出现水平裂缝，随着加载的进行，裂缝沿墙高逐步开裂并最终形成对角阶梯型裂缝(见图3(a)和(b))．对于墙体CW2，沿墙体对角线形成多条贯穿裂缝，并最终形成阶梯型裂缝(见图3(d)和(e))．对于墙体CW3, 阶梯型裂缝偏离墙体的对角线方向(见图3(g)和(h))．由墙体CW1～CW3的失效模型可知，墙体的弯曲机制起主要作用，剪切机制则在墙体整体反应中的作用较小．随着墙体所受竖向压应力的增加，墙体的对角阶梯型裂缝偏离墙体对角线，墙体开裂时间延迟，这主要是由墙体内部黏聚力的增加和块体之间摩擦力的增加所引起的．

(a) CW1

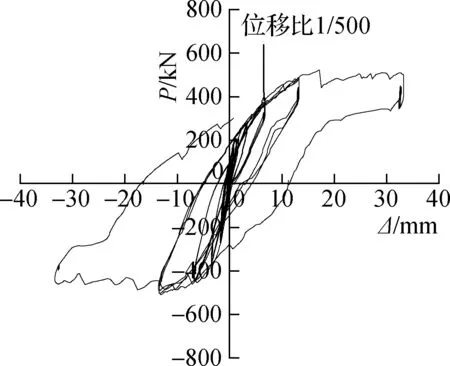
(b) CW2

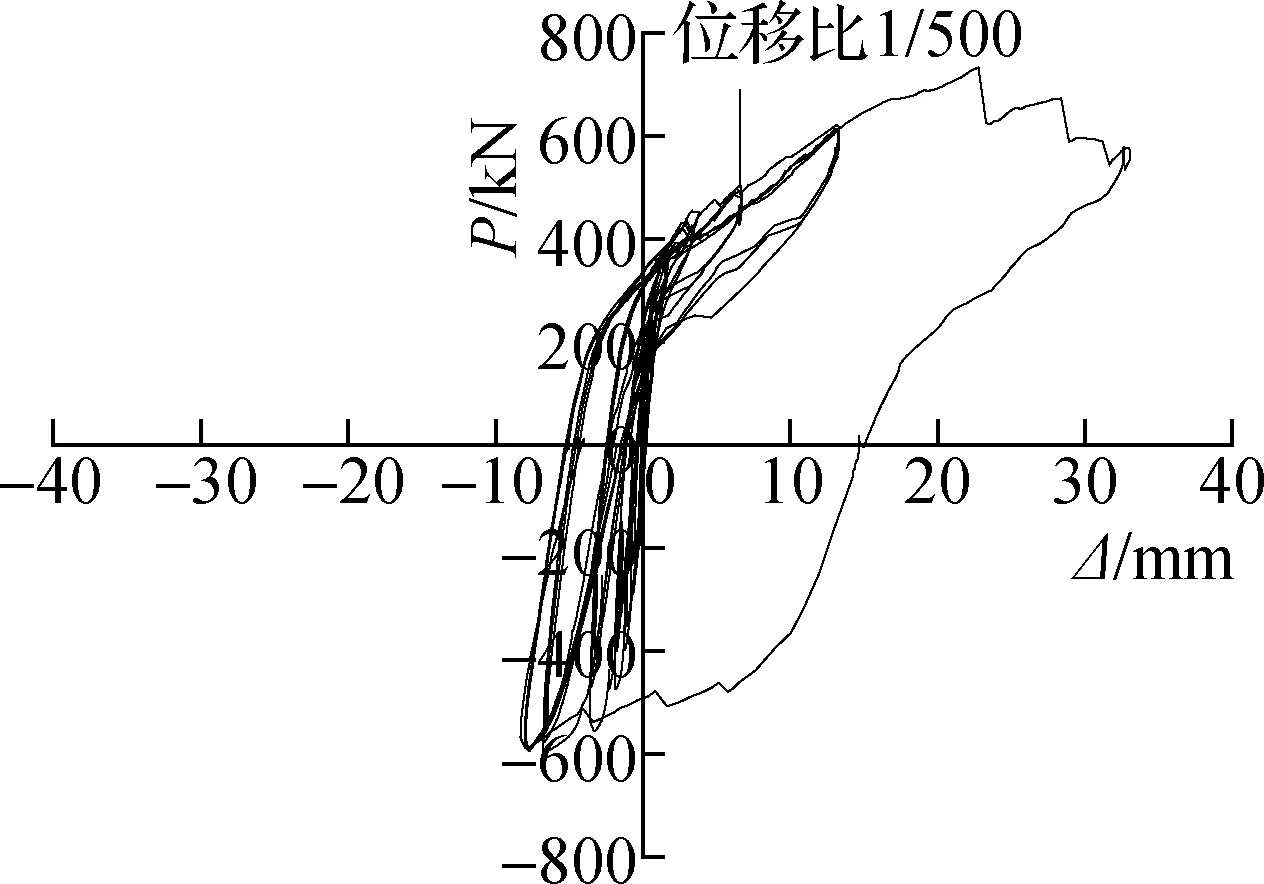
(c) CW3

(d) CW4

(e) CW5

(f) CW6图4 墙体的力-位移滞回曲线

墙体CW1～CW3的滞回曲线表现出了典型的S形特征(见图4(a)～(c))．由图可知，随着竖向压应力的增加，墙体的变形能力减少．对于墙体CW3，变形能力的减少反映出其主要受弯曲破坏控制，与墙体CW1和CW2相比，表现出更大的能量耗散．从位移角1/500开始，随着竖向压应力的增加，3条滞回环均变得相对饱满．

墙体CW4，CW2和CW5主要用于考察不同砂浆强度对有垫片铺浆粗料石墙体的抗震性能影响．墙体CW4的失效由弯曲机制和基底与石块之间的滑移机制控制(见图3(j)和(k))．位移比为1/2 000时，基底出现水平裂缝，随后弥散倾斜的裂缝开始蔓延，最终导致局部化对角裂缝的形成以及中部石块损伤．由图3(d)和(e)可知，墙体CW2的失效模型中大量对角阶梯型裂缝沿石块和砂浆的界面形成，并且伴随角部石块压碎．墙体CW5中部形成剪切裂缝，并沿着对角方向扩展(见图3(m)和(n))．可见，随着墙体砂浆强度的增大，墙体失效模型并未表现出明显规律．

墙体CW2和CW5的滞回曲线均呈典型的S形(见图4(b)和(e))，墙体CW4的滞回曲线则呈梭形(见图4(d))．墙体CW4的滞回环面积明显大于墙体CW2和CW5，这是因为CW4的失效模型为滑移失效，会使砂浆界面产生很大的摩擦耗能．

墙体CW2和CW6用于考察石块尺寸对石砌体墙体抗震性能的影响．对于小尺寸石块CW2，墙体中部出现裂缝并沿对角线方向扩展，且裂缝分布相对均匀(见图3(d)和(e))．对于大尺寸石块CW6，墙体中部出现大量裂缝，同时伴随着角部石块压碎(见图4(p)和(q))．

由图4(b)和(f)可知，墙体CW2和CW6的滞回曲线均呈典型的S形，同时，墙体CW6的变形能力明显较墙体CW2大．

根据墙体的失效模型和滞回曲线特征，可将墙体失效为以下3个阶段：弹性阶段、裂缝形成阶段和摩擦耗能阶段．

2.2 墙体抗震性能

2.2.1 荷载-位移骨架曲线

荷载-位移骨架曲线见图5(a)～(c)．表2给出了屈服点、峰值荷载和极限位移等试验结果．其中，墙体的屈服点通过基于等效能量的弹塑性系统得到[7]，极限位移则为峰值荷载下降至85%时对应的位移值．

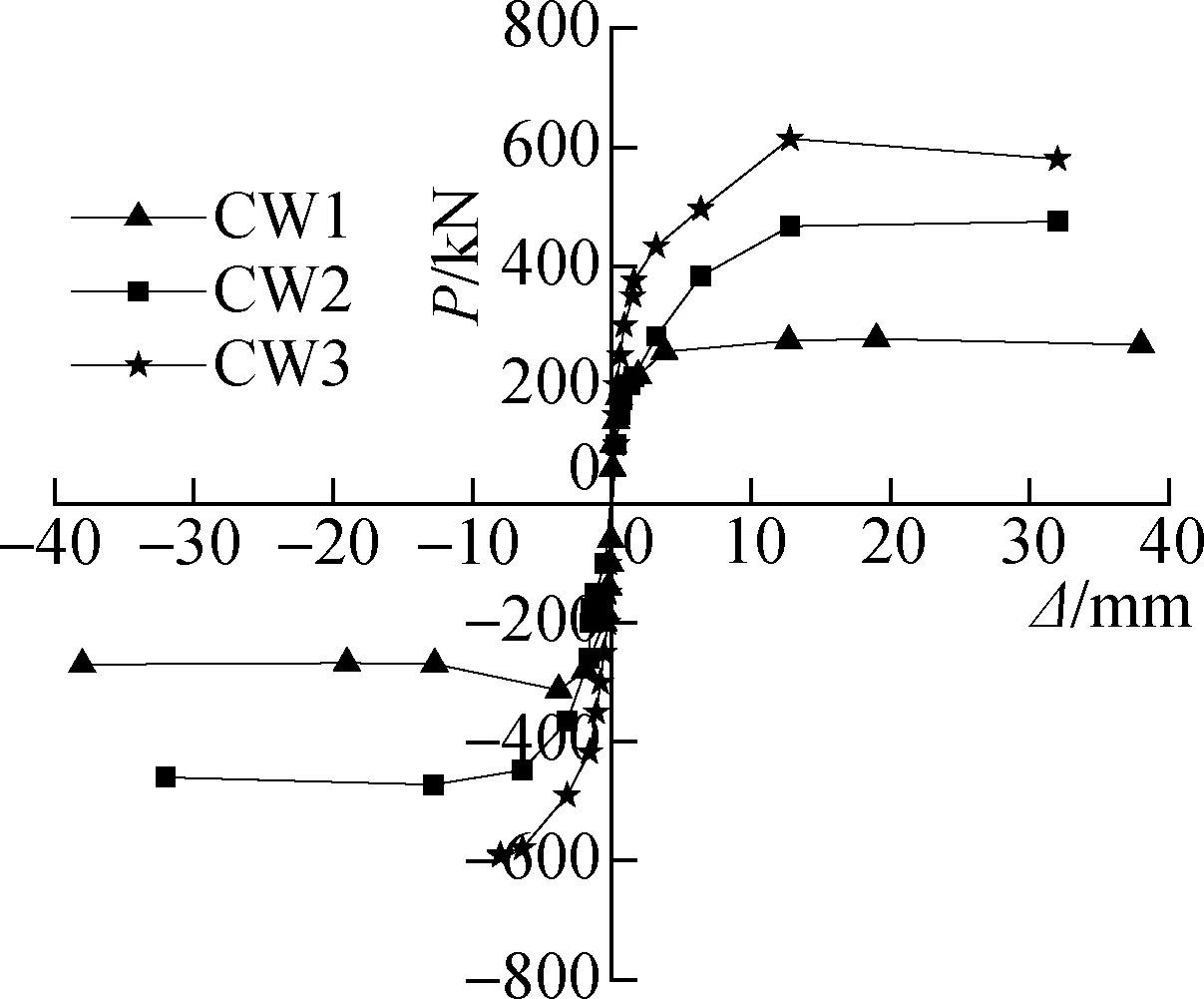
(a) CW1，CW2和CW3

(b) CW2，CW4和CW5

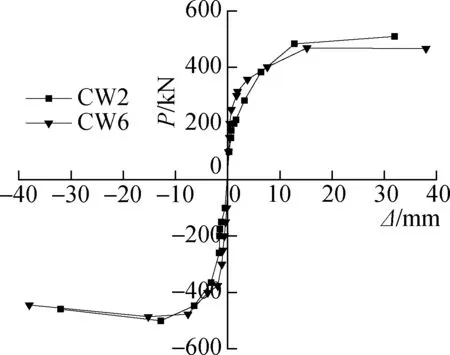
(c) CW2和CW6

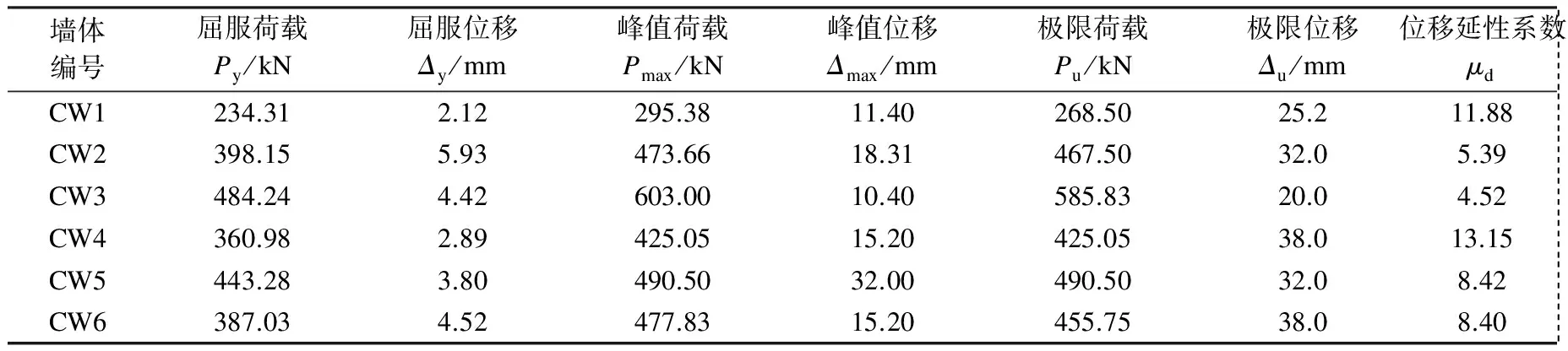
表2 荷载位移包络特征值

由图5(a)可知，随着竖向压应力的增加，墙体CW1～CW3的初始刚度逐渐增加．由表2可知，当竖向压应力从0.25 MPa增加到0.50和0.75 MPa时，屈服荷载、峰值荷载和极限荷载分别增加了69.9%，60.4%，74.1%和106.7%，104.0%，118.2%，而屈服位移、峰值位移和极限位移均表现出先增加后减少的特征．

图5(b)给出了墙体CW2，CW4和CW5的荷载-位移骨架曲线．由图可知，随着砂浆强度的增加，墙体的初始刚度也随之增大．由表2可知，当砂浆强度从2.5 MPa增加到5.0和7.5 MPa时，屈服荷载、峰值荷载和极限荷载分别增加了10.2%，11.4%，9.9%和22.8%，15.4%，15.2%．随着砂浆强度的增加，延性系数表现出先减少后增加的特征，墙体CW2和CW5的峰值位移较墙体CW4分别增加了20.3%和110.5%．

图5(c)给出了墙体CW2和CW6的荷载-位移骨架曲线．由图可知，增加石块尺寸可以增加墙体的初始刚度．墙体CW6的位移延性系数较墙体CW2增加55.8%．

2.2.2 刚度退化

采用文献[8]中的计算方法，得到墙体刚度退化和加载位移的关系(见图6)．由图可知，在推力方向，随着竖向压应力的增加，墙体CW2和CW3的有效刚度较墙体CW1退化得快，在拉力方向也表现出相似的趋势．对于墙体CW4，CW2和CW5，随着砂浆强度的增加，推力方向和拉力方向均呈现出相似的退化趋势．墙体CW4发生滑移失效模型，导致其初始刚度大于墙体CW2，但小于墙体CW5．对于具有不同石块尺寸的墙体CW6和CW2，初始刚度基本一致，刚度退化趋势也相似．对于所有墙体，以加载位移为变量的幂指数曲线可用于表示每一片墙体的刚度退化趋势．

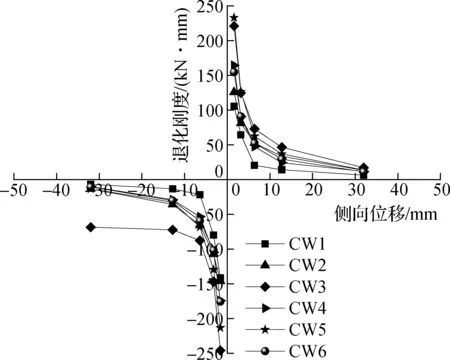
图6 墙体的刚度退化曲线

2.2.3 能量耗散能力

根据荷载-位移滞回曲线，每一次循环的能量耗散可用滞回环所包围的面积来计算．累计耗能与位移的关系见图7．由图可知，当墙体的位移比小于1/250时，随着竖向压应力的增加，墙体的能量耗散逐渐增加；当位移比大于1/250时，墙体CW2和CW3的能量耗散几乎一致，均大于墙体CW1．

对于具有不同砂浆强度的墙体CW2，CW4和CW5，墙体CW4为滑移失效模型，其耗能能力大于墙体CW2和CW5，说明界面粗糙和含有石垫片的砂浆能产生较高的摩擦耗能能力．墙体CW2和CW5的耗能能力随着砂浆强度的增加而增加(见图7)，墙体CW5的累计耗能为墙体CW2的1.15～4.82倍．

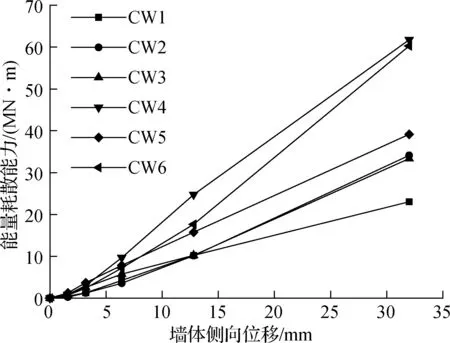
图7 墙体的能量耗散能力曲线

对比具有不同尺寸石块的墙体CW2和CW6发现，能量耗散能力随着石块尺寸的增加而增加；墙体CW6的累计能量耗散能力为墙体CW2的1.73～2.73倍(见图7)，表明大尺寸石块墙体对耗能能力具有积极的影响．

2.2.4 等效黏滞阻尼系数

等效黏滞阻尼系数是定义结构系统阻尼行为的参数[9]．由表3可知，在屈服荷载、极限荷载和失效荷载作用下，墙体的等效黏滞阻尼系数随着荷载的增大而逐渐增加，这表明墙体的能量耗散能力随位移增加而增加．

表3 不同荷载下等效黏滞阻尼系数

对比墙体CW1，CW2和CW3可以发现，当竖向压应力从0.25 MPa增加到0.50和0.75 MPa时，墙体的失效荷载等效黏滞阻尼系数分别增加了41.2% 和52.7%．

对比墙体CW4，CW2和CW5可以发现，当砂浆强度从2.5 MPa增加到5.0和7.5 MPa时，失效荷载等效黏滞阻尼系数随着砂浆强度的增加而逐渐减小．同时，具有滑移失效模型的CW4墙体(砂浆强度最小)的失效荷载等效黏滞阻尼系数最大．

对于墙体CW2和CW6，带有大尺寸石块的墙体CW6的失效荷载等效黏滞阻尼系数比小尺寸石块墙体CW2的失效荷载等效黏滞阻尼系数大51.8%，而且CW6的失效荷载等效黏滞阻尼系数最大．

3 墙体承载力的简化计算

一般情况下，墙体的承载力计算是基于库伦摩擦力准则计算的．另一种计算墙体承载力的公式是基于Turnšek和Sheppard准则[10]得到的，此准则下墙体剪切裂缝开裂时的墙体承载力公式为

式中，Hs为墙体的承载力；σ为墙体的竖向压应力；l为墙体的长度；t为墙宽；b为剪力分配系数[10].

根据规范[11]，黏结强度与砂浆强度有关，即

式中，c为黏结强度；k为调整系数；fm为砂浆强度．

根据文献[12]可以计算得到墙体的抗压强度和简化Turnšek’s模型公式中的墙体抗拉强度．在表4中，μ为摩擦系数，fc为墙体的抗压强度，墙体CW2, CW4和CW5的抗拉强度分别为0.26，0.22和0.27 MPa．

表4 有垫片铺浆砌筑粗料石墙体力学性质

对于具有不同竖向压应力的墙体CW1～CW3，基于简化Turnšek’s模型的墙体承载力公式可以预测墙体抗剪强度．由图8(a)可知，墙体承载力试验值与计算值的最大误差仅为1%．由图8(b)可知，基于简化Turnsek’s模型的墙体承载力的预测公式仅对墙体CW2和CW5有效，而对于墙体CW4，其预测则明显偏离试验值，究其原因在于，墙体CW4发生了剪切滑移失效，而Turnšek’s模型是基于对角剪切裂缝情况计算的．

4 结论

1) 对于所测试的高宽比为定值的墙体，其失效模型明显依赖于竖向压应力和石块体尺寸．

2) 墙体的延性系数随着竖向压应力的增加而减少，随着石块体尺寸的增大而增加；当块体长度从500 mm增加到1 000 mm时，位移延性系数增加了55.8%．砂浆强度对墙体延性系数的影响并没有显示出规律性．

3) 增加竖向压应力可以明显增加墙体的屈服荷载、峰值荷载和极限荷载，增加砂浆强度对墙体抗剪强度提升的效果则不明显．在低砂浆强度和低竖向压应力同时作用下，墙体容易发生滑移弯剪失效．发生滑移弯剪失效的墙体的耗能能力明显比发生弯剪失效模式的墙体高，这主要是因为在发生滑移弯剪失效的墙体中，粗糙的石块表面和包含石垫片的砂浆能够充分发挥摩擦耗能能力并产生较高的摩擦耗能．

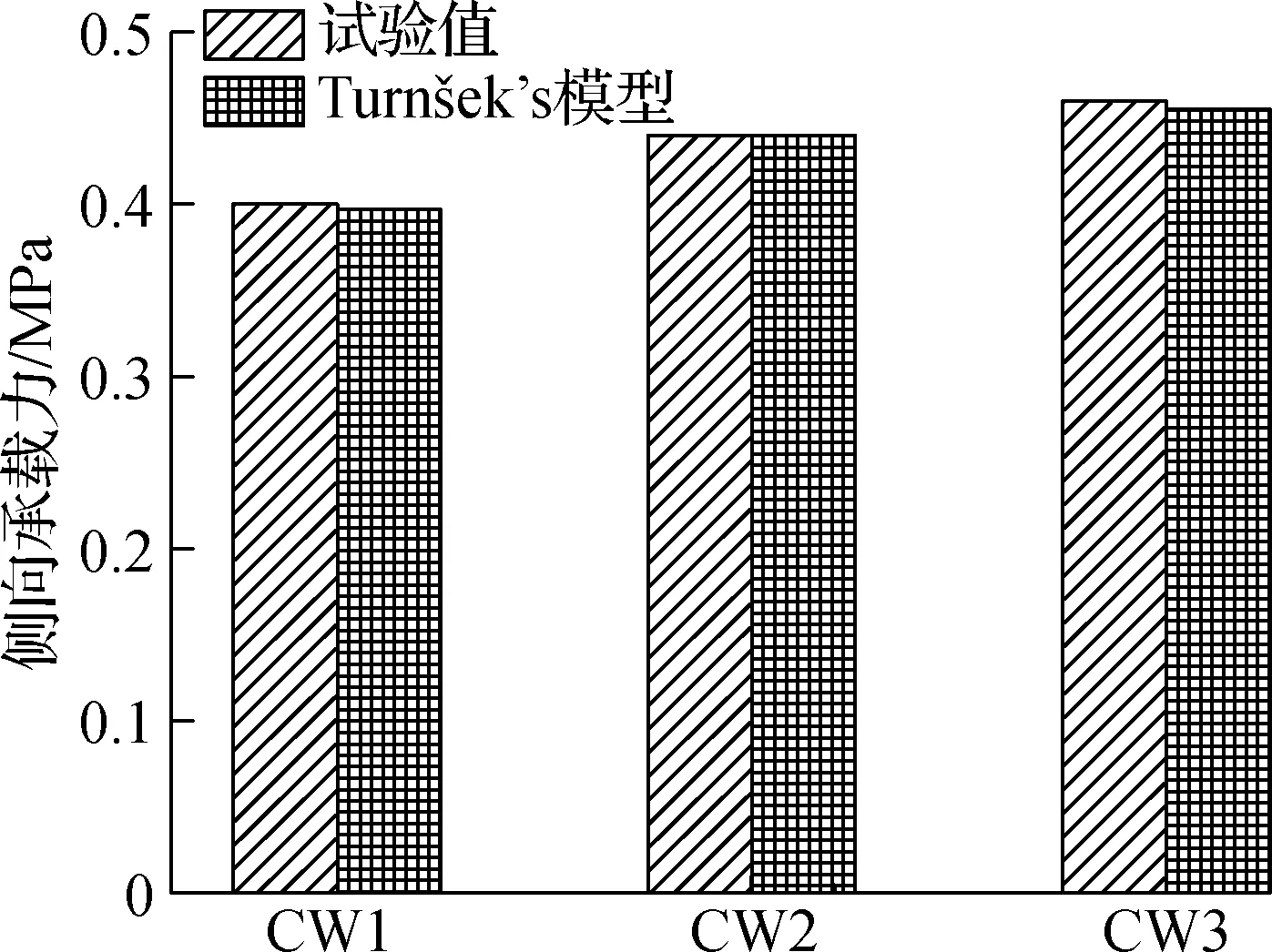
(a) CW1, CW2和CW3

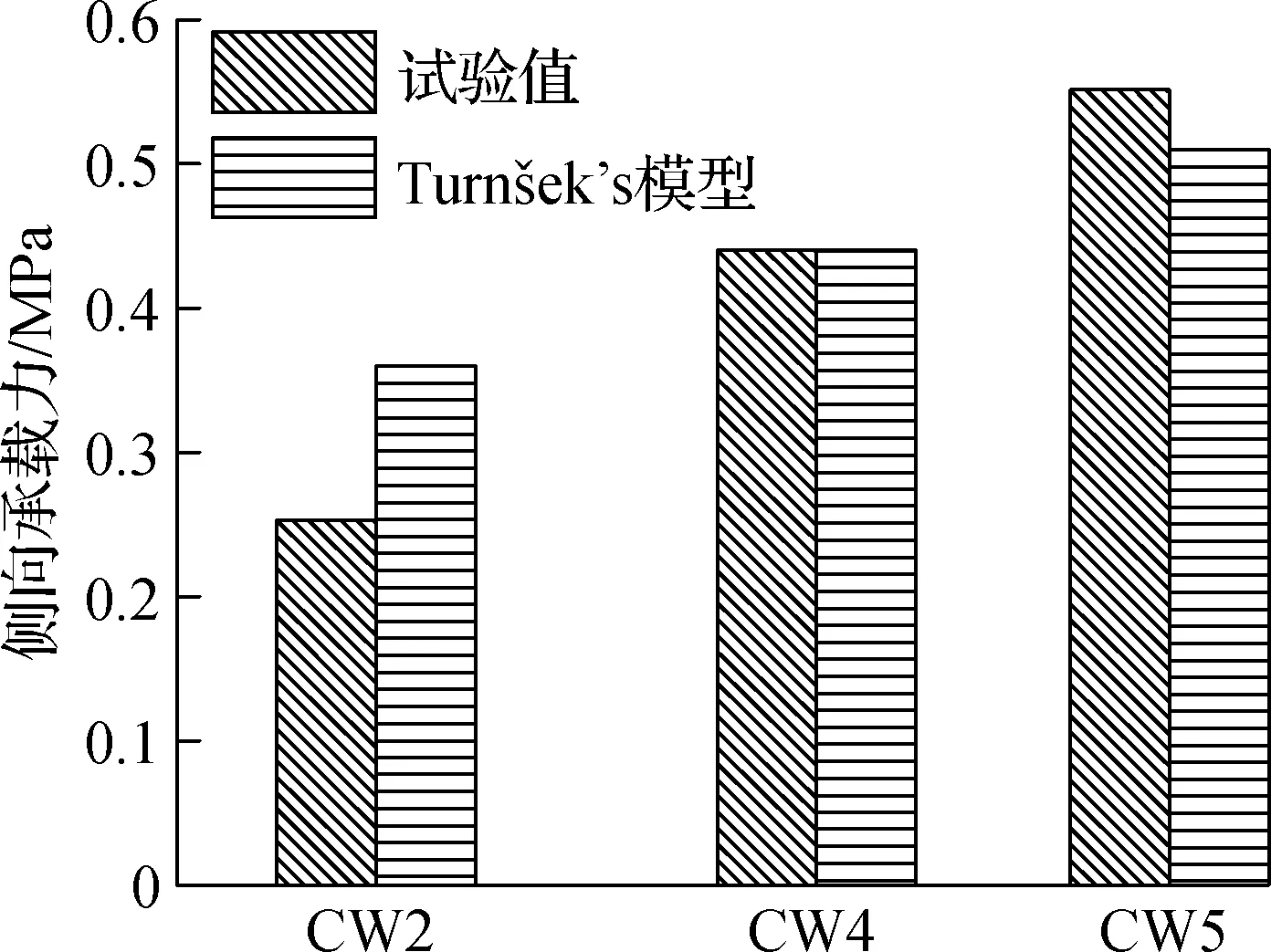
(b) CW2, CW4和CW5图8 墙体承载力试验值与计算值对比

4) 简化的Turnšek’s模型计算方法可以合理预测产生弯剪破坏模式下墙体的侧向承载力，但不能合理预测发生滑移弯剪失效下墙体的侧向承载力，究其原因在于，简化Turnšek’s模型是基于弯剪失效模型假设的．

参考文献(References)

[1] 郭子雄, 柴振岭, 胡奕东,等. 条石砌筑石墙抗震性能试验研究[J]. 建筑结构学报, 2011,32(3): 57-63. DOI: 10. 14006/ j. jzjgxb. 2011. 03. 008.

Guo Zixiong, Chai Zhenling, Hu Yidong, et al. Experimental study on seismic behavior of stone masonry walls[J].JournalofBuildingStructures, 2011,32(3): 57-63. DOI:10.14006/ j. jzjgxb. 2011. 03. 008. (in Chinese)

[2] 郭子雄, 柴振岭, 胡奕东,等. 机器切割料石砌筑石墙灰缝构造及抗震性能试验研究[J]. 建筑结构学报, 2011,32(3): 64-68. DOI :10.14006/ j. jzjgxb. 2011.03.009.

Guo Zixiong, Chai Zhenling, Hu Yidong, et al. Experimental study on seismic behavior and mortar joint detail of machine-sawing stone masonry wall [J],JournalofBuildingStructures, 2011,32(3): 64-68. DOI:10.14006/ j. jzjgxb. 2011.03.009. (in Chinese)

[3] 徐天航, 郭子雄, 柴振岭,等. 钢筋网片改性砂浆加固石砌体墙抗震性能试验研究[J].建筑结构学报, 2016,37(12): 120-125. DOI:10.14006/j.tmgcxb.2016.12.015.

Xu Tianhang, Guo Zixiong, Cai Zhenling et al. Experimental study on seismic behavior of stone masonry walls strengthened with steel meshed modified cement mortar [J].JournalofBuildingStructures, 2016,37(12): 120-125. DOI:10.14006/j.tmgcxb.2016.12.015. (in Chinese)

[4] 郭子雄, 柴振岭, 胡奕东,等. 嵌缝加固条石砌筑石墙抗震性能试验研究[J]. 土木工程学报, 2010(s1): 136-141. DOI:10.15951/j.tmgcxb.2010.s1.096.

Guo Zixiong, Chai Zhenling, Hu Yidong, et al. Study on seismic behavior of stone walls strengthened by mounting bars in bed joints [J].ChinaCivilEngineeringJournal, 2010(s1): 136-141. DOI:10.15951/j.tmgcxb.2010.s1.096. (in Chinese)

[5] Vasconcelos G, Lourenço P B. In-plane experimental behavior of stone masonry walls under cyclic loading [J].JournalofStructuralEngineering, 2009,135(10): 1269-1277. DOI:10.1061/(ASCE)ST.1943-541X.0000053.

[6] Silva B,Dalla Benetta M, da Porto F, et al. Experimental assessment of in-plane behaviour of three-leaf stone masonry walls[J].ConstructionandBuildingMaterials, 2014,53: 149-161. DOI:10.1016/j.conbuildmat.2013.11.084.

[7] Park R. Ductility evaluation from laboratory and analytical testing[C]//Proceedingsofthe9thWorldConferenceonEarthquakeEngineering. Tokyo, Japan, 1998,8:605-616.

[8] Ma G, Huang L, Yan L, et al. Experimental performance of reinforced double H-block masonry shear walls under cyclic loading[J].Materials&Structures, 2016,50(1):70. DOI: 10.1617/s11527-016-0943-0.

[9] Jacobsen L S. Steady forced vibration as influenced by damping[J].TransactionsoftheAmericanSocietyofMechanicalEngineers, 1930,52(1): 169-191.

[10] Turnšek V, Sheppard P. The shear andexural resistance of masonry walls[C]//ProceedingsofInternationalResearchConferenceonEarthquakeEngineering. Skopje, Macedonia, 1981: 517-573.

[11] 中华人民共和国建设部. GB50003—2011砌体结构抗震设计规范[S].北京：建筑工业出版社,2009.

[12] 赵娜.东南地区粗料石墙抗震性能的试验研究[D].南京:东南大学土木工程学院,2013.