浅谈高中数学中导数的应用

◎方国飞

引言：从现阶段的高中数学教学情况来看，学生们学习数学的兴趣并不高，其重要原因就在于高中数学知识比较复杂，学生理解起来比较困难。很多高中学生对数学学习都产生了一种恐惧心理，不知道怎样去学，经常以“依葫芦画瓢”的方法去解答数学题，因此所取得的效果并不理想。所以对于高中学生来说，可以对他们的数学解题思想进行改变，通过导数对相关问题进行解决，利用数形结合的思想，提升他们的做题速度与做题质量，进而提高他们的数学成绩。

一、通过导数解决函数问题

利用导数可以对函数图像的变化规律进行研究，进而对它的单调性进行准确判断。如果f（x）在区间M内可导，并且对于定义域内∀x∈M，都有 f′（x）≥0，那么 f（x）在该区间内为单调递增函数；反之如果 f（x）在区间M内可导，并且对于定义域内∀x∈M，都有 f′（x）≤0，那么 f（x）在该区间内为单调递减函数。另外，通过导数，也可以对函数最值问题进行有效解决。函数最值指的是在某区间M内的最大值以及最小值，利用导数的思想，借助函数图像，就可以对函数最值问题进行有效研究［1］。

二、通过导数解决不等式问题

根据最近几年的高考情况来看，不等式问题具有思维量大以及综合性强等特点，属于历年高考的重点与难点。通过导数对不等式进行证明，实际上就是通过函数和不等式之间的关系，在等价变形之后，按照不等式的特征，对相应函数进行构造，在导数运算的基础上，对函数单调性进行判断，将不等式问题转化成函数问题，进而对其进行有效解决［2］。比如对于下面这道不等式问题：

证明：ex＞1+x（x＞0）

在这道数学题中，我们可以根据函数单调性和导数之间的关系，将不等式和导数进行有效结合。首先需要对函数f（x）进行构造，即f（x）=ex-1-x，然后再对函数 f（x）进行求导，进而得到 f′（x），对其图像进行观察，当x＞0时，其导数图像在x轴上方，也就是说函数在（0，+∞）上为单调递增函数，进而得知当x＞0时，函数f（x）＞f（0）=0，最后得到ex＞1+x。

三、通过导数解决数列问题

高中数学数列问题也是高考必考内容，并且占有较大分值。在对数列问题进行解答时，我们可以将数列当成一种特殊函数，其特殊性主要体现在自变量是正整数，因此可以在函数与数列之间关系的基础上，通过导数对数列问题进行快速解决［3］，比如对于下面这道数列问题：

求数列：1+2a+3a2+4a3+··· +nan-1的和。（其中a≠0，a≠1）

在这道数学题当中，我们可以知道nan-1为an的导数，也就是说（an）′=nan-1，我们可以设数列bn=an，那么可以对数列{b}n的前n项和进行计算，即，之后再将等式两边对a进行求导，就会得到：

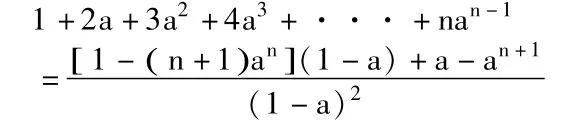
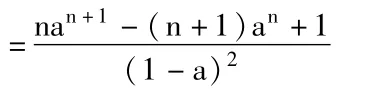
四、通过导数解决实际问题

对于导数而言，不仅可以对函数问题、不等式以及数列等问题进行解决，同时也可以对实际问题进行有效解决。对于学生来说，学习数学的最主要目的是通过数学知识对一些生活当中的问题进行有效解决，所以教师在教学过程中，需要对学生解题意识、解题能力以及解题方法等进行培养，如此一来，不仅可以提高学生的数学成绩，同时也锻炼了他们的数学应用能力［4］。比如对于下面这道数学题：

某企业在对产品进行生产时，已知每天所生产的次品数m是关于每天产量n的函数，当n≤100时，，当 n＞100时，m=n，如果该企业每卖出一件正品，那么就会获利L元，如果生产一件次品，那么就会损失元，当企业想要获得最大利润时，那么每天的产量应该是多少？

在这道数学题当中，我们首先需要对日产量、正品数以及次品数等进行明确，然后再对利润目标函数进行建立，最后对日产量进行计算。

由题意我们可知，m属于次品数，那么在n件产品中，正品数应为n-m，设每日获利总数是 D（n），那么，则，设 D′（n）=0，我们可以得到，再根据n≤100时，，当 n＞100时，m=n，我们可以知道，当n＞100时，所有的产品都属于次品，企业就会产生损失，因此，只有在n≤100的范围内对最佳日产量进行计算，根据，可以得到n约等于89.4，又因为n应该为正整数，因此n的值应为89或者是90，但是由于 D（89）=79.11L，D（90）=70.09L，因此当 n的值为89的时候，D（n）取得最大值，也就是说当企业的日产量为89时，所获利润最大。

结论：总而言之，对于导数而言，不仅是一种数学知识，同时也是一种解题工具、解题思想，解题方法，具有一定的数学价值，为学生提供了新的解题思路，对学生数学学习具有重要意义。因此对于高中数学教师而言，在日常教学中，应该更多从函数问题、不等式问题、数列问题以及实际问题等方面对导数进行合理应用，培养学生的导数思想，进而提高他们做数学题的速度与质量，为他们后续的数学学习奠定基础。

［1］陈展潘.基于导数及其应用浅析高中数学教学［J］.数理化学习（教研版），2017（7）.

［2］许楚滨.基于高等数学指导的高中数学教学实践与思考——以高中《导数及其应用》为例［J］.考试周刊，2017（42）：131-132.

［3］曹云辉.浅谈高中数学中导数的应用［J］.小品文选刊：下，2015（6）：107-107.

［4］陈展潘.基于导数及其应用浅析高中数学教学［J］.数理化学习（教研版），2017（7）.