基于数学核心素养的深度学习实践初探——以“平面向量的分解定理”概念教学为例

◎汪园娣

基于数学核心素养的深度学习是指基于数学核心素养之上的理解学习，学习者能够批判性的学习新的思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，作出决策和解决问题。基于数学核心素养的深度学习是围绕数学抽象、逻辑推理、数学建模、数学运算、直观想象和数学分析六大核心内容［1］，引起学生的高级思维和认知，从而形成对知识的理解和迁移，最终培养学生的批判性思维和创新意识。笔者以“平面向量的分解定理”一课概念教学为例，结合教学实践，以深度学习理论为指导，在课堂教学中探索一套适应于新高考背景下基于数学核心素养的深度学习模式。

教学目标

以探究的形式体验平面向量分解定理的发现和形成过程；

理解平面向量分解定理，体会由特殊到一般的思想，感悟数学的化归思想。

教学重点和难点

重点：平面向量的分解定理

难点：平面向量分解定理的发现和形成过程

教学过程

本节课导入环节，遵循学生的认知规律，在原有的认知体系中，根据已学内容向量的坐标直接导入。［2］通过课堂对话，回顾坐标的形成过程，得出基于两个基本单位向量的向量的正交分解，为本课探究做铺垫。

环节一 坐标导入

提问1：平面任一的坐标怎样表示？回顾向量的坐标表示的由来。

提问2：向量的坐标表示（代数角度），是通过怎样的向量分解（几何角度）实现的？

提问3：平面内任一向量的正交分解唯一吗？

本环节注重元认知发展，开展深度学习，鼓励学生以探究的方式和合作的模式进行新知识和信息与新问题的解决。注重学生对于现有知识的反思，并强调新知识内化之后，与固有知识结构之间的联系。

环节二 特例过渡

适当改变上述正交分解的条件，通过数学活动的开展，体验一般情形下正交分解的过程。

数学活动：上述正交分解中的“两个基本单位向量”改为“给定两个互相垂直的非零”，能否进行分解？分解有何特点？

数学发现：“互相垂直”条件改变可以分解吗？

数学活动的开展，让学生发现基于给定两个互相垂直的非零向量，可以进行正交分解。对于知识的处理，是基于学生对知识的理解，由特殊到一般，循序渐进，在此基础上进行知识的获取和解决问题的策略。深度学习的必要前提是学生对于知识有着比较浓厚的兴趣，有探究的欲求。

环节三 定理探索

基于寻找向量分解的条件，进一步引导，激发学生进一步探索的欲望。

（一） 数学发现

探究1：除正交分解外，你还可以对平向量进行怎样的分解？

探究2：对于满足什么条件的两个给定向量，平面内任一向量可以分解？

数学发现：类比向量的正交分解，当“两个互相垂直的”变成“给定平面上两个不平行向量”，你有什么发现？

给定一组不垂直的非零向量，亲身经历向量分解的过程，目的在于寻找向量进行分解的条件。将已有认知结构中知识迁移作用于其它情境中，特殊到一般，通过类比发现，给定平面上两个不平行向量，该平面上任一向量都可以表示成这两个不平行向量的线性组合。

（二）数学体验

活动一 给定两个方向，将一个分解成两个向量的和.

活动二是平面内两个不平行的向量，是该平面内的任意一个非零向量，之间的关系.

通过数学发现，得出向量分解的条件；开展数学活动，经历平面向量的分解。初步形成：平面内的任意一个非零都可以表示成这两个不平行的线性组合，即分解可行.

（三）数学探究

从两个特殊向量出发，师生共同完成这两个特殊向量的分解，得出可以分解且唯一。

探究三 当平面上两个不平行的取定时，任一向量的分解唯一吗？

探究的思路始终遵循学生的认知结构，由已知到未知，由特殊到一般，进行逻辑推理，得出当平面上两个不平行的向量取定时，任一向量的分解唯一。学生结合自身的内在需求对学习材料进行比较深刻的思考和探究，通过使用与学习材料相适应的学习方法，对知识进行批判性的接收和创造性的使用，从而实现学习的真正意义，达到深度学习的效果。

环节四 定理形成

学生通过定理探索，经历数学发现、数学体验、数学探究，概括平面向量分解定理：

探究一 条件中“不平行向量”，改为“平行向量”，如何？

探究二两绳子可以以任意角度悬挂同一重物，重物因为具有重力，会对两绳子产生拉伸效果。

思考：两根绳子的悬挂的角度不同，重力分解的结果如何？

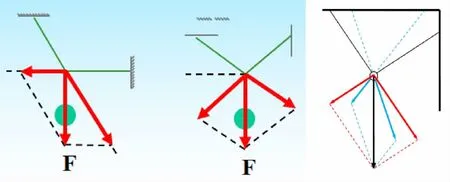
探究三对于给定的一组基，向量的分解是否唯一？

以探究的形式体会定理的涵义，从物理实例出发，在熟悉的问题情境中，经历物理问题数学化的过程，感悟其中蕴含的数学原理，加深数学理解，得出平面上任一向量可以有无穷多种分解，即有无数组基，且对给定的一组基分解唯一。

环节五 定理应用

通过定理探索，得出平面向量分解定理，如何夯实该定理，通过下面的几个实例来实现。

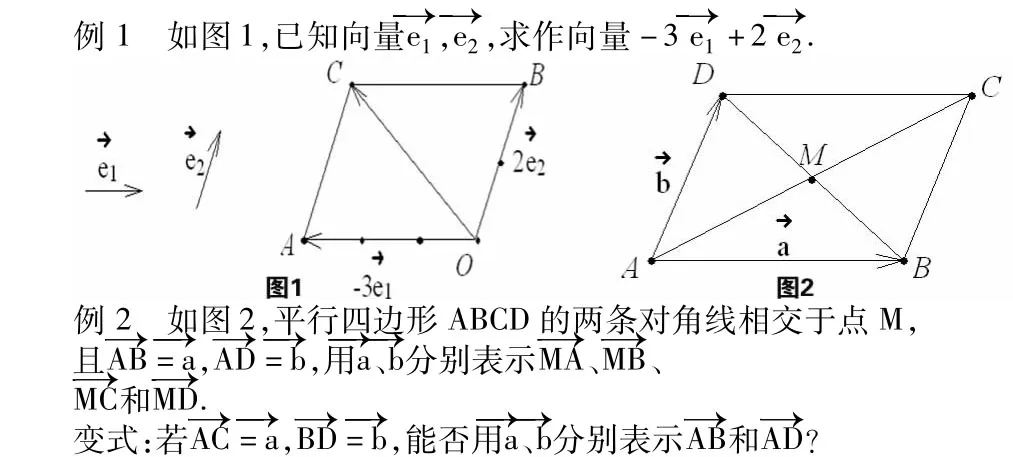
解决实际问题，体会基向量思想在运算化简中的作用，可以让向量运算更加有目的性，体会平面向量分解定理的意义。深度学习，注重对于知识的解释与剖析，并且随着知识种类的不同而有着不同的内化模式。

教学后记：以探究的形式体验平面向量分解定理的发现和形成过程，教学紧紧围绕向量分解展开。在教学过程中，学生无论经验的积淀、基本思想的形成，还是数学抽象能力、逻辑推理、数学建模的培养，都离不开学生的主动参与、独立思考和亲身实践，离不开学生的自我建构。因此，学生发展所必需的数学核心素养是学生亲身经历数学化活动之后所积淀和升华的产物，这种产物对学生在数学上的全面、和谐、可持续发展起决定作用。［3］

课堂教学采用探究形式，有利于培养学生的发现问题解决问题的能力，通过亲身实践探索获得的知识，实现自我建构，以实现深度学习。在实际操作中，学生思维一旦打开，探究问题方向多样，而易脱离教学主线，影响教学进度的推进，需要提前预想到多种可能情况，合理安排探究内容和时间，以达到更好的教学效果。

［1］教育部课程标准修订组.普通高中各学科核心素养一览表 ［EB/OL］.http：//learning.sohu.com/20160422/n445632409.shtml

［2］吴秀娟，张浩，倪厂清.基于反思的深度学习：内涵与过程［J］.电化教育研究，2014（12）：23-28.33.

［3］孔凡哲.学会数学化切实提升数学学科素养［J］.小学数学教师，2015（6）：孔凡哲.学会数学化切实提升数学学科素养［J］.小学数学教与学，2015，（9）.