极限思维法在初中物理解题中的妙用

◎雷良青

物理作为一门极为重要的科学学科，能够帮助学生更好地理解生活中的一些自然现象的发生。物理因其严谨性、抽象性和逻辑性，对于学生的思维能力有着一定的要求，学生学习的难度也会相较其他科目有所增加，即使是保证课堂的高效率，但是在遇到练习题时，还是会发现无从下手。此时就需要教师在教学过程中，帮助学生在最短的时间内找到最合适、最快速的解题方式，从而让学生在解题时达到事半功倍的效果。

一、极限思维法

极限法是一种科学的思维方法，假若某物理量在某一区间内是单调连续变化的，我们可以将该物理量或它的变化过程和现象外推到该区域内的极限情况（或极端值），使物理问题的本质迅速暴露出来，再根据已知的经验事实很快得出规律性的认识或作出正确的判断，从而能使求解过程简单、直观，这种思维方法称为极限思维法。极限法在进行某些物理过程的分析时，具有独特作用，恰当应用极限法能提高解题效率，使问题化难为易，化繁为简，思路灵活，判断准确。

二、意义

1.找到解题突破口 对于初学物理的学生来说，不是课堂的听课效率有多高，对知识的掌握有多细致就可以解决做题时遇到的困难，有时候使学生对于题目不能够理解，从而无法找到突破口去思考解答。加之受到老师教学思维的限制，更加想不到其他方法去快速发现题目的突破口。而极限思维法却为学生提供了一种快速发现题目突破口的解题的思维方式。

该问题如果用极限法来分析，解决起来就简单得多了。题意是沿图1中虚线截取，那我们不妨截去更多一些，把水面以下的部分全部截去，又会怎样呢？因为剩下的木块密度不变，它仍然会处于漂浮状态，既然是漂浮，必然有一部分浸入水中，所以，截取之后木头会下沉一些，故选C。

2.突破思维定式 为了追求更高的学习效率和学习成绩，老师在教学过程中会告诉学生一套固定的解题方式和解题思维，以至于限制了学生的拓展性思维，学生的解题方式都是千篇一律。对于物理这门学科，形成固定的思维定式后，会影响后期对于物理的学习掌握程度，很难将物理知识灵活的应用于解题中，若是能在教学过程中将极限思维法渗透其中，帮助学生更好地掌握，就能够使学生有效地突破定向思维，大大提高学习和解题效率。

3.提高解题效率 利用目前掌握的思维方法确实可以解决一些物理题目，但是所用的解法传统而复杂，需要利用大量的物理公式，无形中增加了运算量，也增加了错误率，有可能因为记错了一个公式或者算错了一个数字导致整道题的错误，不免觉得不值得。在讲究速度的同时也要讲究做题的正确率，只有选择简单的解题方法，才能够提高解题效率。

三、极限思维法的妙用

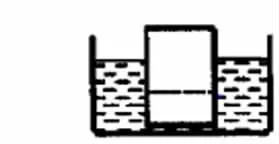
例1：如图1所示，密度均匀的木块漂浮在水面上，现沿虚线将下部分截去，则剩下的部分将？

A.上浮一些 B.静止不动

C.下沉一些 D.无法确定

本题常规解法如下：由于木块的密度保持不变，不论是否截取一部分，该木块都处于漂浮状态。根据物体漂浮条件F=G得：ρgV=ρgV，V/V的值是一定的，所以V/V的值也应该是一定的。当沿虚线将虚线以下部分截去之后，假设木块保持静止不动，此时V减小，而V不变，所以V/V的值减小，故不可能静止不动，而应该下沉一些，保持V/V的比值不变，故选C。

例2.倾角为θ的斜面上有一静止的小球（细线与斜面平行），请问小球对斜面的压力随着倾角θ的变化会发生变化吗？

极限法解题：

当θ=0°时，该小球静止在水平面上，小球的重力和地面对小球的支持力是一对平衡力，所以重力等于地面对小球的支持力；又因为小球对地面的压力和地面对小球的支持力是一对相互作用力，所以小球对地面的压力等于地面对小球的支持力。所以当θ=0°时，小球对水平面的压力等于小球自身的重力。

当θ=90°时，该小球在竖直方向所受的重力和细线的拉力是一对平衡力，在水平方向该小球对右侧接触面的压力为零。假如小球对右侧竖直面存在压力，由于力的作用是相互的，那么，右侧竖直面对该小球必然存在一个反方向的支持力。那么，该小球在水平方向就只受一个向左的支持力，就不可能在θ=90°保持静止平衡。因此当θ=90°时，该小球对接触面的压力为零（不存在压力）。

综上所述，小球对斜面的压力是随着倾角θ的变化而变化的，压力随着倾角θ的增大而减小。

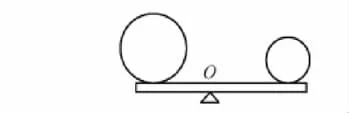
例3：如图所示，杠杆处于平衡状态，如果将物体A和B同时向靠近支点的方向移动相同的距离，下列判断正确的是（）

A.杠杆仍能平衡 B.杠杆不能平衡，左端下沉

C.杠杆不能平衡，右端下沉D.无法确定

故此题选C。

极限法解题：该问题用极限法来分析，需要找到题目中的关键条件，就是“物体A和B同时向靠近支点的方向移动相同的距离”，那我们就让它们移动的距离为OC长，此时杠杆左边的力臂为零，由图示可知OC＜OD，杠杆右边的力臂不为零，所以杠杆左边的力矩为零，右边的力矩不为零，因此杠杆将向右端倾斜。故此题选c。

结束语：利用极限思维法结合适合自身的学习方式，可以帮助学习物理时达到事半功倍的效果。对于初次接触物理初中生来说，找不到合适的思维方式会加大学习这门科目的难度，从而对这门科目失去信心。利用极限思维法，突破思维定式，举一反三，化繁为简，出奇制胜，激发学生对物理的学习兴趣，增强学生的创新能力，大大提高解题效率。但是并非所有的知识点都可以运用到极限思维法来解题，因此要合理运用，深度剖析，降低学习物理的难度。

［1］陆文彬.极限思维法在初中物理解题中的妙用.《数理化解题研究》，2017年08期.

［2］公丕宝.极限思维法在初中物理解题中的运用探析.《考试周刊》2018年28期.