平行班级教学质量的比较

◎何义华 肖芳兰

教学质量是学校的生命线。在学校狠抓教学质量的同时，教学质量的测评越发引起老师们的强烈关注。目前，对教学质量的测评都是基于一些简单的指标，如平均分、优秀率、及格率等。尽管这些指标有一定的参考价值，但是在实际操作时还是会显得不科学，比如平均分对低分和高分敏感、优秀率只对高分敏感、及格率对低分太不敏感。在许多的重点学校中都会存在平行班级，对于平行班级教学质量的测评更加需要客观、科学的评价体系。所以建立科学、合理、客观的教学质量测评体系显得尤为重要。通常，评价教学质量的主要依据就是学生的考试成绩，如何分析评价平行班级的考试成绩就是本文要研究的主要问题。

所谓平行班级，就是学习成绩相近的班级。事实上，不管学校有没有重点班，基本上学校都会存在若干个平行班级。重点班之间可算是平行班级、非重点班之间也可算是平行班级，所不同的是平行的层次。由于平行班级的考试成绩差异本来就不大，定性分析测评、几个简单的指标量化测评都不足已为教学决策提供有力的依据。对于这些平行班级之间教学质量的比较需要更加精准、稳健的测评体系。为了更有效地解决平行班级教学质量的评价问题，基于数理统计的视角引入生物学中的等效性检验来进行比较。

一、等效性检验的理论

等效性检验的研究始于20世纪60年代，但是直到90年代才由Westlake将其广泛运用到生物制药上。历经数十年的发展，等效性检验已经相当成熟，并得到了广泛的推广和应用。在临床研究中，等效性检验的原假设是“治疗方案一与治疗方案二不等效”，而备择假设是“治疗方案一与治疗方案二等效”。这种等效性检验不同于一般的差异性检验，它不是针对点进行检验而是针对区间来进行检验。下面以药物临床研究为例介绍等效性检验理论。

临床等效性检验主要考察不同治疗方法下临床结果上是否相似或相近，即不同治疗方法是否等效。以两组对照试验的均值比较为例，不妨假设：试验组（test）和对照组（control）的样本容量分别为nT和nC，总体均值分别为μT，μC；试验所得样本的样本均值分别为；两组试验被认为相似或相近的等效临界值为Δ（治疗效果相似或相近的度量测度不超过Δ，则称Δ为等效临界值）的标准差，其中两样本合并后的方差。那么所得的等效性检验情况如下：

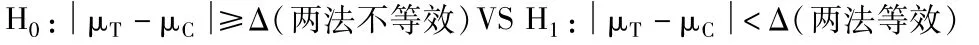
取检验统计量，在原假设下此检验统计量近似服从t分布，故此种检验也称t检验。

当时，则两法肯定不等效；当已知μT＞μC且μT-μC≥Δ时，两法肯定也不等效；当已知μT＜μC且μC-μT≥Δ时，两法肯定仍不等效；时，则拒绝原假设，即认为两法是等效的。若给定假设检验的显著性水平为α及t检验的自由度为ν=nT+nC-2，那么当时，则拒绝原假设且认为两法等效；当时，则没有理由拒绝原假设且认为两法不等效。有关等效性检验的具体知识和详细理论基础可参看医学统计学的相关书籍，在此不再详细介绍。

二、教学质量的等效性检验

教学质量是否能进行等效性评价呢？从医学的角度来看，如果把学生当成是药物试验的样本对象，那么老师就可以看成是一种药物，两个班级考试的成绩就是样本的取值。此时，对两个平行班级教学质量的评价就等价于比较两组样本。一般地，平行班级的起始成绩都是相近的，不妨假设一次正常考试的分值都应该服从正态分布。那么，在正常情况下两个班级考试成绩就符合等效性检验的理论条件，从而能够利用等效性检验来进行教学质量的测评。

当等效性检验的样本值取学生成绩时，我们只要将两个平行班级分别看成试验班（test）和对照班（control）即可。在实际中，两个平行班的学生情况肯定不会完全一样，那么根据统计学的理论应该尽可能取更多的学生进行对照试验。但是一个班的学生不可能有很多，我们只能从全班人数出发，最多用全班学生的成绩去进行对比从而推断出哪个班的教学质量好。大家都清楚平行班级的教学质量一般不是考试的平均分就能完全衡量的，在文中引用一个理想评价指标来衡量教学质量。从现今的实际出发，这个理想评价指标一般都是取所有学生考试的平均分，只是文中的这个平均分是衡量两班教学质量的理想平均分，并不是用某次考试的成绩来计算而是用某次考试的平均分来推断这个理想平均分。通常认为，考试平均分越高理想平均分也应该越高，考试平均分较低理想平均分也应该较低。当然具体地操作时，两班参与试验的学生成绩应该进行排序并且按照序号依次对照（高分和高分对照、低分与低分对照），那么参照临床等效性检验不妨记：

①试验班（test）和对照班（control）的学生人数分别为nT和nC；

②两班教学质量的理想评价指标（学生考试的理想平均分）分别为μT和 μC；

④两班被认为教学质量相当的平均分的最大差额或所设定的等效临界值为Δ；

⑤为的标准差，其中两样本合并后的方差。

那么所得的教学质量的等效性检验情况如下：

H0：（两班教学质量不等效） VS（两班教学质量等效）同样地，取检验统计量，在原假设下此检验统计量仍近似服从t分布，故也可以用t检验来检验两班的教学质量是否等效。根据不同的比较需要，在若给定假设检验的显著性水平为α及自由度为ν=nT+nC-2时，有如下检验结果：

①当时，则两班教学质量肯定不等效，故需要检验时统计量t的值都是非负的：当时，试验班的教学质量高于对照班的教学质量；当时，对照班的教学质量高于试验班的教学质量。

②当时，则没有理由拒绝原假设，即认为两法不等效：当已知μT＞μC且μT-μC≥Δ时，显然不需要检验也知道试验班的教学质量高于对照班的教学质量；当已知μT＜μC且μC-μT≥Δ时，不需要检验也知道对照班的教学质量高于试验班的教学质量。

③当时，且记给定假设检验的显著性水平为α及自由度为ν=nT+nC-2，那么当时，则拒绝原假设且认为两法等效；当时，则接受原假设且认为两法不等效。

三、等效临界值的确定

等效临界值的确定是一个非常重要的问题，到底平行班级理想平均成绩相差几分认为教学质量相当呢？如果这个等效临界值Δ设定过大，则不能比较出平行班级的教学质量；如果Δ过小就变成了点检验，不能很好地包容非老师因素导致的教学质量偏差。在理论上有文献指出当Δ难以确定时，可考虑取个标准差或者对照组均值的较适宜。在临床医学上Δ的取值是由经验丰富的专家来决定，并且经过反复论证最后确定。那么，在教学评价中同样可以借鉴相同的方法确定等效临界值。

四、教学质量评价实例

实例：同一个老师所教的平行班级在某次考试的成绩如下：

A班成绩（60人）：

100，97，93，92，92，91，89，86，86，85，84，83，82，80，80，80，79，79，77，76，74，73，68，66，64，63，63，62，62，61，60，59，58，55，55，55，54，54，53，53，48，48，46，44，43，42，41，38，38，38，38，36，32，29，29，23，21，21，17

B班成绩（60人）：

97，93，93，93，91，89，89，87，86，86，86，85，85，83，83，81，81，81，80，79，79，78，78，77，75，74，73，71，69，68，65，63，63，58，56，54，54，50，49，47，47，45，45，43，40，40，40，38，37，36，34，29，28，28，25，17，17，13，12，10

假设A班为试验班、B班为对照班，经计算可得：

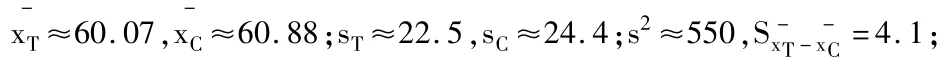
①当给定 Δ=5，α=0.05时，，故认为两班教学质量不等效；当给定Δ=5，α=0.01时，98，仍可得两班教学质量不等效。

②当给定Δ=10，α=0.05时，，可得两班教学质量不等效；当给定Δ=10，α=0.01时，，可得两班教学质量等效。

③当给定Δ=15，α=0.05时，，可得两班教学质量等效；当给定Δ=10，α=0.01时，，仍可得两班教学质量等效。

由此可见，教学质量于同一个老师、不同班级也是有差异的。如果正确的选择了等效临界值Δ和显著性水平α，利用等效性检验的方法就能够很好地度量出两个班级的教学质量；如果Δ和α的确定不是很科学、合理，那么即使用等效性检验也不会得出合理的结论。对于不同老师之间的教学质量评价仍然可以采用等效性检验的方法，只要准确的确定Δ和α的值即可。

等效性检验理论还在发展，等效性检验的应用也在逐渐拓展。文中说明了等效性检验应用于教学评价的合理性。从统计学的视觉出发，很好地解决了平行班级教学质量的评价问题，对于任意两个班级或老师之间的教学质量评价可以同样的进行等效性检验，甚至是非劣性检验等。