抓事物本质 促思维素质——例谈复数在解题中的应用

◎王爱华

我们知道在数学解题中，揭示知识点的本质，题目的特征、结构等，是解题的一个关键，如：复数，就其本质来说，它是在实数的基础上扩充而来，任意复数，无论是由实部与虚部两部分组成的，还是由模与幅角相结合的，都是由一对实数确定，就其表现形式，可用复平面上的点、复平面上的向量来表示，它们之间不仅存在对应关系，且可相互转化，有着丰富的内涵。只要充分认识复数的本质，在复数集内就可化“实”为“虚”，“虚”中求“实”。因此，“虚”“实”互求，既相对，又相辅。今略举几例说明之。

一、在求三角函数值中的应用

【例】已知 α、β、γ是公差为2π/3的等差数列，求 sinα+sinβ+sinγ与 cosα+cosβ+cosγ的值。

分析：α、β、γ之间的关系为 β=α+2π/3，γ=β+2π/3=α+4π/3，而所求式子为三个角的同名函数之和，由此，启发我们运用复数三角式的加法与乘法来处理比较好。

解：设 Z1=cosα+isinα，则

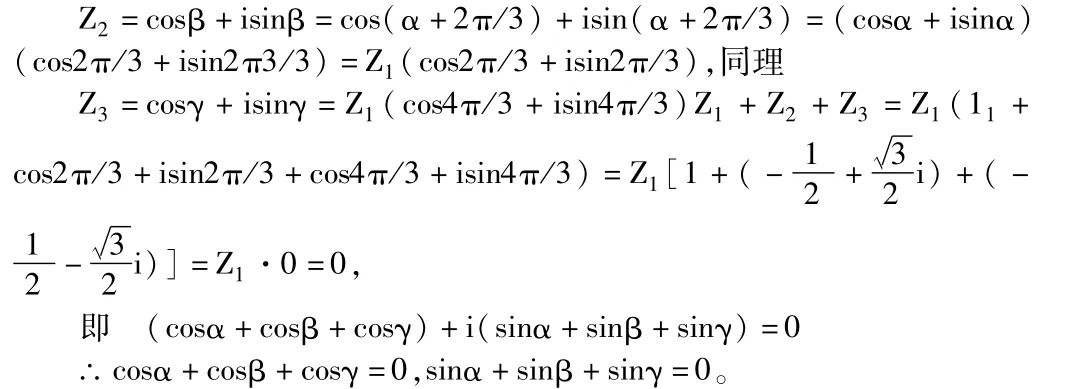
点评：这里应用了复数三角式化简角呈规律性变化的两弦函数和的式子这一本质特征，很凑效，它能把正弦函数和的值以及余弦函数和的值同时求出。

二、在证明不等式中的应用

【例】a、b、c∈R，且 a+b+c＞0，

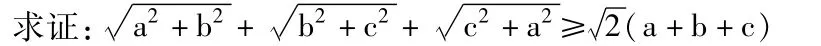
分析：由题目结构特征，联想到复数模，再联想到复数不等式，通过模的运算及复数不等式得证。

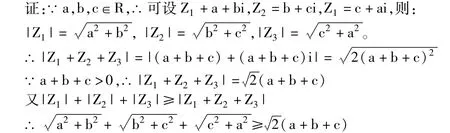
点评：由于题目的特征、结构，引入复数的模及复数不等式（实质上是一个实数不等式），应用了复数的模的本质特征，使得一个较繁的无理不等式化繁为简。

三、在求轨迹方程中的应用

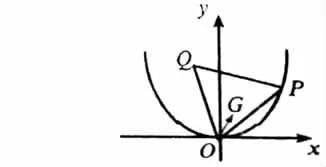
【例】在抛物线y=x2上有一个动点P，以OP为一边，按逆时针方向作正ΔOPQ，求此三角形中的心G的轨迹方程。

分析：这是一个线段旋转问题，OG可视为OP旋转，并按比例缩短而得，从而联想到复数乘法的几何意义，再通过复数相等找到了第一动点与第二动点的关系，问题得以解决。

解：建立直角坐标系如图，设 G（x，y），P（x′y′）在复平面上作向量，则按逆时针方向转30°，模缩为原来的即得到，两者的对应复数有关系式

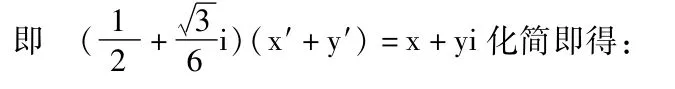
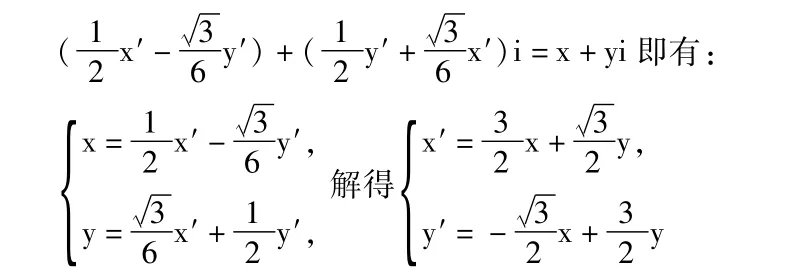
代入点P满足的方程y=x2化简即得点G的轨迹方程为：9x2+6。

点评：这是一个旋转问题，一般来说，紧扣复数乘法的几何意义和复数相等的充要条件可“实”“虚”互化这一本质特征，就便于解决问题。

四、在证明三角恒等式中的应用

【例】求证：

点评：这里通过观察思考题目的结构特征，充分应用了复数运算和复数相等的本质特征。

五、在求反三角函数值中的应用

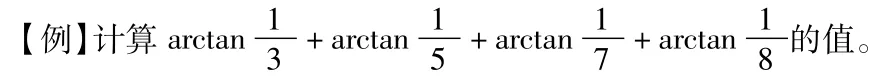
分析：实质上这是一个实数问题，但实数包含于复数，且题中所含的量在复数中具有辐角主值的意义，数学中用构造某些复数，使其辐角成为所求式子中的角度，从而通过复数运算性质而求角。

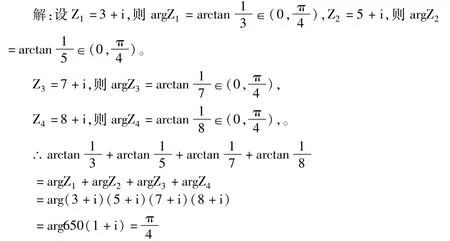
点评：构造复数使它们的辐角分别为组成题中的各角，应用了复数运算的本质特征，从而化“实”为“虚”去解题，再从“虚”中求“实”求得辐角。

关于复数在解题中的应用题很多，以上只举了其中常见的几种，以说明抓住事物的本质，去解决矛盾这一观点。笔者认为，在教学中，不论传授知识、还是传授方法、培养能力等方面，只要坚持这一辨证的观点，不仅有利益提高教育教学质量，而且在培养学生思维素质方面都进入了更深一个层次，无疑对提高学生的数学素质起着重要的促进作用。