初中数学实验情境的创设与实施
2018-06-08
(江苏省昆山市葛江中学)
数学实验是指为研究与获得某种数学理论,验证某种数学猜想,解决某种数学问题,运用一定的物质手段,在特定的实验条件下进行的一种探索活动.依据初中数学实验的特点,教学中借助现代化教学手段,遵循数学实验情境创设的原则,创设有效的数学实验情境,强调课堂教学的实践探索,重视学生的感受和体验,关注对学生核心能力的培养.寻找数学实验情境实施的最佳着陆点,追溯知识产生、迁移和应用的过程,解决认知与情感、动脑与动手、抽象思维与形象思维等发展的不平衡问题,实现“融情导悟”,积极探索有效的教学补充形式,改善教学方法,使教师的教学水平和教学效果不断提升.
一、遵循情境创设的原则,创设有效的数学实验情境
教学活动是师生积极参与、交往互动、共同发展的过程.新课程要贯彻“学生为主体,教师为主导”的理念,让学生有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.初中数学实验必须明确:问题由谁提、方法由谁想、感想由谁悟.因此,在初中数学实验情境创设中坚持“四项基本原则”:(1)目的性,即情境创设的目的是否明确;(2)主体性,即创设的情境能否引起学生学习的主动性和积极性;(3)真实性,即如何展示数学实验情境创设的真实性;(4)有效性,即是否能真正地引发学生的思维活动.
案例1:在“比例的基本性质”的教学中,教师创设这样一个数学实验情境:在阳光下如何利用自己的身高测出学校旗杆的高度?该情境创设的内容真实、目的明确.由于旗杆无法直接测量,引发学生深入思考和探索,并在常规思维的基础上进行拓展.利用同一时刻、同一地点,在太阳光照射下,物高和影长成比例解决问题.实验中,学生用创新思维解决实际问题,从而丰富学生的认知结构,克服习惯性思维,培养思维的变通性.
创设有效的数学实验情境,有利于学生循着知识产生的脉络准确把握学习内容,帮助学生顺利实现知识的迁移和应用,使学生在学习中产生强烈的情感共鸣,增强实践体验.
二、创设不同的数学实验情境,发展学生的核心能力
针对初中数学实验教学的基本类型,即操作型数学实验教学、思维型数学实验教学、多媒体模拟数学实验教学,根据教学需要创设各种不同的情境(如生活化情境、问题化情境、模拟化情境、探索性情境等),并加以实施,指导学生开展质疑、想象、操作、探索、验证等实践活动,发展学生的数学核心能力,体现情境创设对初中数学实验教学的补充功能.
1.创设生活化情境,在分析生活现象中获得数学体验,培养创新思维
数学生活化的意义在于找到学习的起点,使学生的思维得到已有经验的支持,帮助学生内化已掌握的知识.
案例2:在苏科版《义务教育教科书·数学》(以下统称“苏科版教材”)七年级上册“6.3余角 补角对顶角”的教学中,可设计如下的探究活动.
如图1,长江护堤底部用石块堆积而成,量角器无法伸入护堤底部,如何测量护堤坡面的倾斜角∠1的度数?

图1
学生通过讨论,获得如下解决问题的两种方法.方法1:如图2,在地面上反向延长∠1的一边,与∠1的另一边构成∠2,则∠1+∠2=180°.测量出∠2的度数即可以计算出∠1的度数,由此引入互补的概念.方法2:如图3,过∠1的顶点作地面的垂线,即以∠1在地面上的一边为直角边作直角,另一直角边与∠1的另一边构成∠2,则∠1+∠2=90°.测量∠2的度数即可以计算出∠1的度数,由此引入互余的概念.

图2

图3
数学概念(知识)来源于生活,又服务于生活.通过创设生活化的数学实验情境,引导学生交流解决实际问题的方法,引入互补、互余的概念,提高学生的学习兴趣,培养创新思维,使学生获得学习数学的成就感.
2.创设问题化情境,在解决问题中感受知识的生成,培养抽象概括能力
教师通过巧妙地设置情境,让学生产生好奇,激发学生的兴趣,结合探究活动发现数学规律,对新知识的学习会起到事半功倍的效果.
案例3:教学苏科版教材七年级上册“乘方”的内容时,有一个“探究活动”:将一张报纸对折,再对折,……直到无法对折为止,你对折多少次?用算式表示你已对折出来的报纸层数.
学生将手中的纸按要求对折,并记录每一次对折后纸张的层数,列出如下的表格,根据表格发现数据变化的规律,利用规律引入乘方概念.

2 3 4 5 6 n 对折次数纸张层数1 2 4=22 8=23 16=24 32=25 64=26……2n
数学规律的抽象性通常以“直观”的想法为背景.通过实验操作让学生发现数学规律,感受知识的生成,培养学生的抽象概括能力.
3.创设模拟化情境,运用多媒体技术呈现运动变化过程,丰富空间观念,培养数据处理能力
空间观念是指在空间感知的基础上形成的,关于物体的形状、大小和相互位置关系,通过观察、想象、比较、综合、抽象分析,不断向前发展的认识客观事物的过程.利用多媒体技术进行模拟实验,可以演示物体运动的轨迹,使抽象的、不易理解的知识变得生动、有趣,丰富空间感受,使所学的知识化难为易.
案例4:苏科版教材九年级上册第53页“操作与思考”是探究圆周角的性质,教材以三种不同的位置关系(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)分别进行推理论证,得到结论“圆周角的度数等于它所对弧上的圆心角度数的一半”.对于这个问题,可以借助几何画板软件展示图形的变化过程(微信扫描本文标题上方二维码即可观看变化过程):如图4,变化1,点C沿圆周运动,改变圆心O与圆周角的位置关系;变化2,点B沿圆周运动,改变角的大小;变化3,圆的大小变化.对每种情况即时显示弧度、圆心角、圆周角对应的数值,由数字揭示圆周角的度数与它所对弧的圆心角度数之间的数量关系.
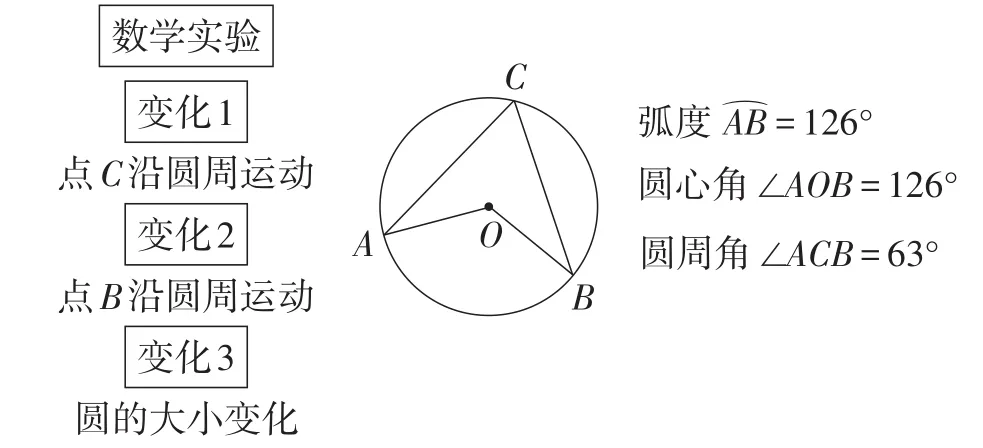
图4
利用多媒体技术辅助重组资源,提供有助于培养学生数感的情境活动,使学生具有应用数字表示具体数据和数量关系的能力,具有选择适当的方法实施计算的经验.
4.创设探索性情境,在表述实验结论中凸显理性分析,发展逻辑推理能力
通过创设合理的数学实验情境,采用一系列探究性活动,发现数据的变化,探究数量之间的关系,提出猜想,并进行证明或验证,是数学教学过程的完整体现.
案例5:在苏科版教材八年级下册实验课“数格点,算面积”的教学中,可设计问题情境:兄弟分地.
如图5,哥哥说:“我的地一圈只有15棵树,而弟弟的地一圈有17棵树,弟弟的面积大!”弟弟说:“我的地里只有16棵树,而哥哥的地里有17棵树,哥哥的面积大!”到底谁的话有道理?
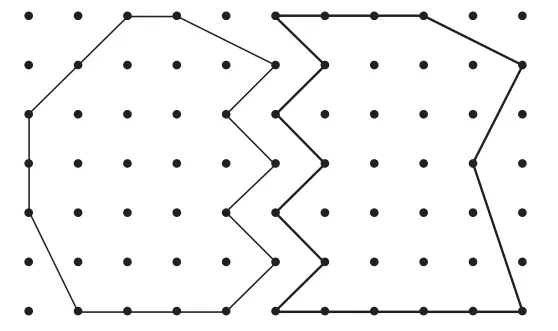
图5
为探究格点多边形的面积S与多边形边上的格点数L,以及它内部的格点数N之间的数量关系,设计4个探究活动,即当格点多边形内部的格点数N=0,1,2,3时,分别探究格点多边形的面积S与边上的格点数L之间的数量关系,发现S与N,L之间存在数量关系然后对动手操作、猜想获得的结论,再利用“数学工具”及计算进行逻辑验证,最后利用实验结论解决问题,在此过程中培养学生严谨的理性分析能力.
在实验条件下进行探索,用数量关系表述实验结论,并进行验证,从感性上升到理性,这体现了数学的实验味,加强了学生的数学理解能力,发展了逻辑推理能力.
三、寻找数学实验情境实施的最佳着陆点,实现“融情导悟”
研究初中数学实验情境的实施过程,寻找和探索数学实验情境实施的最佳切入点、最佳时机和最佳形式,检验情境创设的有效性,可以体现初中数学实验情境创设在不同着陆点的功能,实现“以境推动课堂,以情激发思考”.
1.设在教材知识的点睛处,落实重点
初中阶段,教材上知识的形成是学生通过推理验证获得的,是以学生已有的几何直观和生活经验为先导,利用数学实验可以先探索,发现结论,再对结论进行推理论证.
案例6:针对三角形内角和定理的证明,可以采用多种实验方式获得不同的证明方法.
方法1:可以把一个三角形纸片的三个内角剪下,在同一顶点处拼成一个平角;方法2:通过折纸实验,折成一个矩形(如图6),使三角形三个内角在同一顶点处拼成一个平角;方法3:利用平行线的性质构造同位角或内错角,实现“移角”,使角度大小不变、位置改变,因而将三角形三个内角集中在一起,或利用同旁内角的关系来进行证明(如图7),以此落实学习重点.
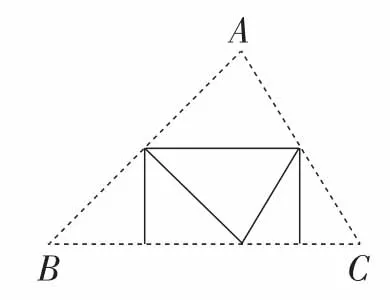
图6
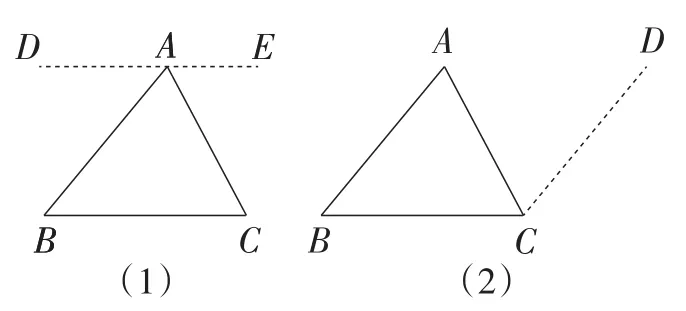
图7
将数学实验情境设在新知引入处,通过操作型数学实验把复杂的数学问题变得简明形象,有助于探索解决问题的思路,预测和检验结论,实现几何直观这一目的.这种情境创设方式在数学学习中会发挥重要的作用.
2.设在学生感兴趣的地方,活跃气氛
情境是激发兴趣、点燃探求欲望的火种.在学生感兴趣的地方设置数学实验情境,可以增强学生探究的欲望.
案例7:苏科版教材八年级下册“8.3频率与概率”中有抛掷质地均匀的硬币实验.教材上采用汇总学生的实验数据,通过列表、描点、连线,得到结论:当实验数据很大时,“正面朝上”的频率稳定在0.5左右.学生对此实验的兴趣浓厚.
此时若利用计算机的计算能力,可以在短时间内进行大量的抛掷硬币模拟实验,并且可以随机选择实验次数,为结论的验证提供充分依据.如图8为计算机模拟实验结果,选择抛掷硬币601次,得到“正面朝上”的频数是298,“反面朝上”的频数是303,因此“正面朝上”的频率是49.6%,在优化随机数生成的前提下保证了实验的准确性.
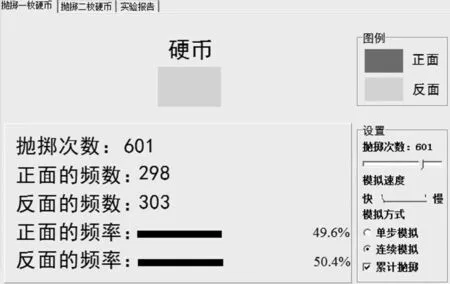
图8
利用计算机模拟抛掷硬币实验,还可以分析抛掷2枚硬币的情况.这在一定程度上既能保证结果和结论的准确性,又能节约大量的人力和物力,发展了学生的数据分析能力.
将数学实验情境设在学生的兴趣点,可利用多媒体技术模拟实验,通过数据分析体验随机性,从中发现规律.这既可以使学生体会到统计需要收集数据,应用数据分析可以解决实际生活中的很多问题,感受统计的实际价值,又活跃了课堂气氛.
3.设在学生思维的集中处,激发思维
以学生为中心、以问题为主线,结合数学实验情境,经过调查研究了解对象信息、分析内在规律后,用数学符号语言的表述建立数学模型解决问题,使学生的思维处于高度激发状态,以此提高学生分析问题和解决问题的能力.
案例8:教学“轴对称”时,可设计“将军饮马”实验.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
对于此问题,如图9所示,将河岸看作一条直线l,选择点A或点B中任意一点作关于直线l的对称点.若选择点A作关于直线l对称点A′,将点A′与点B连接起来,与直线l的交点P即所求的饮马点.根据轴对称性质知点P到A,B两点的距离之和为A′B的长.对于河岸上任意非点P的点P′,其到A′,B两点的距离相当于△A′P′B的两条边P′A′和P′B的和,根据三角形两边之和大于第三边的性质,可以得出PA+PB一定是最短路线.
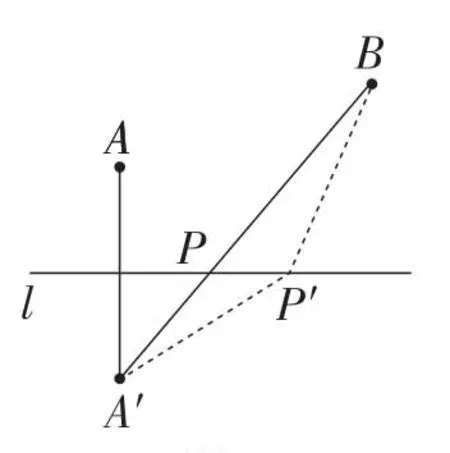
图9
若一个动点在直线上运动,要确定它到直线同侧两个定点距离之和最小的点,可将图形置于平面直角坐标系或不同的几何图形内,结合两点之间线段最短、垂线段最短、线段的平移等知识,通过找点关于线的对称点,将折线转化为直线,从而找到最短路线.
借助数学实验情境,利用数学建模解决问题,可以使学生看到问题的本质,提升分析问题和解决问题的能力.
4.设在学生思维的障碍处,突破难点
当学生思维受阻时,教师可以巧妙地创设数学实验情境,让学生运用已有知识与体验,去分析思考、突破难点、解决问题.
案例9:如图10,竹竿AB的长是2米,斜靠在墙壁AC上,∠ABC=60°.如果竹杆两端A,B分别沿AC,CB方向滑动至点A′,B′,使∠A′B′C=45°,问竹竿的中点D随之运动所经过的路程是多少?
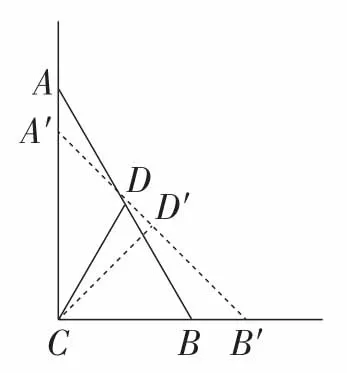
图10
此题的难点在于中点D的运动路线是什么图形?若利用几何画板软件跟踪点的功能进行模拟实验(微信扫描本文标题上方二维码即可观看变化过程),学生可以清楚地观察到,中点D的运动轨迹是一条圆心角为15°、半径为1米的圆弧,从而解决问题.
在学生思维受阻时,教师可以通过创设与实施合适的数学实验情境,利用多媒体技术演示物体的运动轨迹,协调学生的视觉与思维,将问题提炼为概念、法则或公式,找出解决问题的方法,帮助学生突破难点.
创设数学实验情境,需要在数学思维的参与下,通过实践操作、探索交流,从而发现规律,进行验证.在实施过程中,要引导学生体验数学、感受数学和理解数学,发展学生分析问题和解决问题的能力.研究初中数学实验情境的创设与实施,加大了数学教学目标的范围与深度,是新课程改革的体现.
[1]董林伟.数学实验:促进初中生数学学习的一种有效方式[J].中国数学教育(初中版),2012(9):2-5.
[2]杨丽娟.从感性到理性 体现数学的实验味:以数学实验“数格点算面积”教学设计为例[J].中学数学教学,2016(5):9-11.
