如何培养学生的数学阅读能力

（四川省简阳市城北九义校）

数学为其他科学提供了语言、思想和方法，而数学阅读是读者通过数学语言符号获得意义的一种心理过程，是学生主动获取信息、汲取知识、发展数学思维和学习数学语言的重要途径.近年来，需要通过阅读来解决的实际问题在中考中所占的比重越来越大.因此，在教学中必须重视对学生数学阅读能力的培养，落实现代教育所提倡的“终身教育，终身学习”的理念.

那么，如何在教学中培养学生的阅读能力呢？

首先，我们应该认识到，数学阅读不同于看小说，一目十行、泛泛而读是不行的.数学语言高度抽象并且逻辑严密，在阅读中，学生必须通过理解有关的数学语言，分析每个术语之间的逻辑关系，甚至对每个符号都要反复推敲，才能达到理解材料、形成知识结构的目的.其次，数学语言具有精确性.在阅读一段数学材料时，学生必须了解其中的每个概念的精确含义，不能囫囵吞枣，更不能读而不思.这都需要学生在阅读中学会细读、精读，有目的、有重点地读.

根据数学阅读的特点，笔者在教学中采用以下方法，循序渐进地培养学生的阅读能力.

一、创设适合学生的阅读环境

这里的环境有两层含义：首先，要有安静的教学环境，数学阅读需要学生静下心来感知、思考，太“热闹”的环境是不行的；其次，教师要创设能调动学生阅读积极性的问题情境.

案例1：在教学“图形的平移”时，教师可以创设如下的问题情境.

教师给学生出示实际生活中物体平行移动的形象例子，如滑雪运动员在平坦的雪地滑翔、电梯的上下运动、火车在笔直的轨道上奔驰等，并提问：这些运动现象的痕迹有什么共同的特征？这样就把学生的注意力引向了观察图形之间的关系上.通过观察、分析，学生可能会说出下列一些共同属性：它们都是运动的，形状都没有改变，运动轨迹都是在一条线上，等等.得出这些共同属性时，学生在头脑中已经对平移的概念进行了初步概括.接下来，教师就可以引导学生到教材中去寻找答案了.

通过以上方式，不但让学生完成了对“平移”这一概念的认识，而且让学生经历了“问题情境—建立模型—解释应用”的过程，培养了学生的阅读能力，提高了学生的学习兴趣.

二、教会学生正确的数学阅读方法

1.引导学生抓关键字、词

学生在刚开始进行数学阅读时，往往不知道从何入手，很茫然.这时就需要教师做示范，对主要的数学名词、关键的语句、重要的字眼等要重复读，甚至边读边提问，让学生带着问题阅读，有目的、有方向地读.教师示范后，让学生再阅读教材，使他们真正领会本节课的主要内容及重、难点.初步阅读完成后，教师再指导学生阅读例题，让学生自己寻找题目的关键字、词，自主寻找解题的正确思路.这样，一节完整的自学课就形成了，这不仅帮助学生学到了本节课的知识，更培养了学生形成良好的阅读习惯和自学能力.

案例2：在学习一元一次方程时，教材内容呈现较少，如果学生泛泛而读，对知识理解一定不到位.此时教师就要引导学生抓住关键词“一元”“一次”，并提出问题：一元、一次分别是什么意思？有哪些需要注意的问题？让学生有目的、有重点地阅读，才能有的放矢，达到理想的教学效果.当学生基本掌握了一元一次方程的含义后，教师可以再给出一些题目进行巩固.

例判断下列哪些是一元一次方程.

（1）3x+5=7x+2；

（2）2x+3y=6；

（3）y2+2y+1=0；

（4）2x2+9=3x+2x2；

（5）

通过以上步骤，不仅帮助学生顺利掌握了知识，而且对学生理解数学阅读有很好的帮助.

2.在阅读中列提纲

概念教学是初中数学课堂教学的重要组成部分.通过概念教学，可以使学生深刻理解并正确掌握概念.但是，很多学生在学习概念时，不是死记硬背，就是生搬硬套字面意思，不做深入理解，长期下去，会磨灭学习兴趣.对此，教师可以通过列出阅读提纲的方式，指导学生从多角度，有重点、有目的地阅读，加深对新知识的理解.

案例3：在学习分式概念时，仅仅通过“创设情境—阅读教材—小组讨论—归纳总结”等一系列步骤得出概念，可能只是表面的学习，对学生深入理解概念是不够的.在实际教学中，教师可以在学生了解基本概念后，通过设计阅读提纲，从多维度地帮助学生深入理解概念.

例如，在知道分式的概念后，设计如下问题.

（1）分式有意义的条件是什么？

（2）分式为0的含义是什么？

（3）若分式的结果为正，其中的字母系数有什么特征？

（4）若分式的结果为整数，其中的字母系数有什么特征？

根据提纲，指导学生带着问题阅读，极大地提高学生对概念的理解.当学生能理解分式的概念的内涵与外延后，再辅以如下题目.

（1）当x____时，分式无意义.

（2）当x____时，分式的值为0.

（3）当x____时，分式的值为正；

当x___时，分式的值为负．

（4）若分式的结果为整数，则整数x可以是___.

通过以上步骤，学生不仅能很好地理解分式的概念，而且能在学习概念的过程中，学到一定的学习方法.从而培养了良好的数学思维品质，提高思维能力，达到会学、乐学的目的.

3.学会自然语言与数学语言的转化

数学语言具有一定的抽象性，跟自然语言差别很大.很多学生不知道怎样进行数学阅读，一个主要的原因是在数学阅读时，需要频繁转换数学语言和自然语言.数学阅读的过程实质是一个语言转化的过程，是新、旧知识的碰撞与统一的过程.教师要帮助学生掌握数学语言的特点，尤其要指导学生在阅读中学会用数学符号表示自然语言.例如，七年级的学生就经常遇到“甲数比乙数少1”这种类型的题目.由于学生刚刚进入初中，阅读能力薄弱，往往不清楚应该怎样表示两个数的关系，教师就可以做如下的指导.设乙数为x，“比”在这道题目中的数学语言即为“=”，所以甲数就是“等于x少1”，顺理成章的就得出甲数为“x-1”.虽然题目不难，但是体现了数学阅读的一个重要作用，即将阅读内容转化为学生易于接受的语言形式.

案例4：（2015年山东·临沂）定义：给定关于x的函数y，对于该函数图象上任意两点(x1，y1)，(x2，y2)，当x1＜x2时，都有y1＜y2，称该函数为增函数.根据以上定义，可以判断下面所给的函数中，是增函数的有________（填上所有正确答案的序号）.

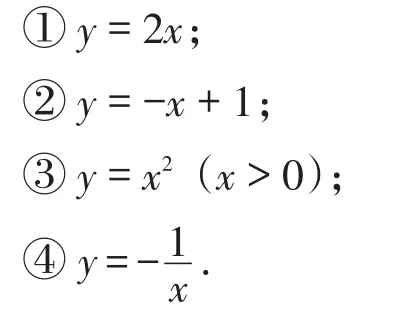
此题需要学生在阅读中进行各种语言的转化，结合一次函数、二次函数、反比例函数的性质，严格按照新定义的要求验证即可.虽然难度不高，但是体现了数学阅读的重要特性，即数学阅读常要求大脑建立起灵活的语言转化机制，这正是数学阅读有别于其他阅读的最主要的方面.

4.读思结合，广采厚积

在教学中，教师还要指导学生在阅读中学会积累加工，认真仔细，勤思多想.加强学生自主学习最为核心的一点就是强化对数学阅读的指导.通过阅读指导，让学生能够理解所学知识，将原有知识融会贯通，抓住重点线索和基本思想方法,养成善于提炼的良好习惯，获得学习再创造的体验过程，增强数学学习能力.尤其是针对近几年中考中出现的与高中知识接轨的题型，教师更应引导学生在阅读中围绕重点和关键点，进行分解、组合、变换处理，抓住问题的本质，进而辨认出其对应的核心知识点，从而顺利解决问题.

案例5：阅读材料，完成下列问题.

解一元二次不等式x2-3x+2＞0，可将原不等式化为(x-1)(x-2)＞0.由有理数的乘法法则“两数相乘，同号得正”，得

解不等式组①，得x＞2；解不等式组②，得x＜1.

所以(x-1)(x-2)＞0的解集为x＞2或x＜1，即一元二次不等式x2-3x+2＞0的解集为x＞2或x＜1．

仿照上述解法，完成下列不等式.

（1）一元二次不等式x2-3x+2＜0的解集为____；

（2）分式不等式的解集为____.

此题看似简单，但实际上对学生在阅读中提炼核心知识点的能力要求比较高.对于第（1）小题，教师应指导学生围绕关键点“两数相乘，同号得正”，展开类比联想“两数相乘，异号得负”，将不等式x2-3x+2＜0转化为从而求出解集为1＜x＜2；对于第（2）小题，不能生搬硬套题目的解法，必须注意到题目形式虽然是分式不等式，但其核心仍然是“两数相乘，同号得正”，才能使问题顺利得到解决.这些都是需要学生在长期阅读中有一定的积累才能解决的.

可见，在教学中教师一定要重视提高学生的数学阅读能力，要指导学生善于积累.针对不同层次的学生，教师要根据学习的需要，有筛选地指导，帮助学生在阅读中广采厚积.而积累贵在引导，教师要多方面指导学生积累方法，提高学生运用数学知识去解决实际问题的能力.

综上所述，重视数学阅读，对于开阔学生的数学视野，发展学生的语言表述能力、概况联想能力、猜测创新能力有着重要的意义.只有通过阅读，不断地掌握新知识，吸收新思想，才能提高学生分析问题、解决问题的能力.我们在教学时，应结合学生的实际，激发学生的数学阅读兴趣，培养学生的阅读能力，为学生的终身发展服务.

［1］李兴贵，幸世强，冯国卫，等.新课程数学阅读教学新论［M］.成都：四川大学出版社，2006.

［2］辛自强.数学中的阅读理解［J］.教育科学研究，2004（9）：49-51.

［3］展秀芬.重视数学阅读 提高学习能力［J］.广西教育_，_2011（6_）：20-21.