基于回归折算法的小样本数控机床可靠性建模

张海波，王 妍

(东北电力大学 机械工程学院，吉林 吉林 132012)

0 引言

随着设计和制造水平的不断提高，中高档数控机床的可靠性水平越来越高，加之更新换代速度快和试验时间的限制，使得收集到的故障数据逐渐减少。传统的可靠性建模方法都依赖于大样本数据，在分析小样本数据时，所得结果往往存在很大的误差。因此，研究在小样本情况下的可靠性建模具有重要的现实意义。

目前，针对小样本数据的可靠性建模方法有修正极大似然估计法、Bayes法、Bootstrap法、Bootstrap-Bayes法等[1-5]。Kan[6]根据Bayes方法，融合专家经验与多源先验信息建立威布尔参数的先验分布，采用网格近似方法计算后验分布，建立可靠性模型。张立敏[7]依靠专家经验得出先验分布函数，通过粒子群优化算法对模型中的尺度参数和形状参数进行估计，采用Bayes法进行了可靠性建模。Bayes法虽能充分利用现存的所有信息，但计算时涉及到大量积分运算，且先验分布确定不好，效果更差。高攀东[8]提出了一种B-MUME法，利用Bootstrap法，扩大样本的数量，采用MUME法对威布尔分布模型的参数进行估计。孙慧玲[9]利用Bootstrap法将样本量进行了自助扩充，再对扩充后的样本进行参数估计。Bootstrap方法过度依赖于子样的情况，不利于参数估计的稳健性。利用参考产品的历史故障数据扩充小样本数据，可充分利用现存的所有信息，使结果更加准确。孙祝岭[10-11]针对航空航天不同环境下试验数据的折算问题，提出了一种回归折算法，能弥补数据少的缺陷，提高数据的利用率，并应用 Monte-Carlo 方法进行仿真模拟来证明其有效性，但并未对威布尔分布进行检验。

本文在此基础上，通过回归折算法，将符合威布尔分布的参考产品的故障数据折算成产品本身的故障数据，扩充成大样本数据，采用经典的可靠性建模方法进行模型的建立，并用Monte-Carlo进行模拟仿真，验证其方法的正确性，并结合具体实例加以说明分析。该方法对于数控机床的小样本可靠性建模，具有重要的工程应用意义。

1 威布尔分布的可靠性模型

早期对数控机床进行可靠性建模时，多采用指数分布作为参数模型，随着研究的深入和发展，威布尔分布被认为能更好的描述数控机床的数据特征[12]。

两参数威布尔分布的分布函数是：

(1)

其中，t为时间；α为尺度参数；β为形状参数。

由威布尔分布函数可知，其可靠度函数、概率密度函数和失效率函数分别为：

(2)

(3)

(4)

欲建立数控机床的可靠性模型，必先确定参数α和β。需要通过大量的故障数据分析获得其估计值。然而在小样本情况下，无法通过经典建模法求得准确的模型，因此借助于回归折算法扩大其样本量，以提高评估结果的准确性。

2 回归折算法

回归折算方法其基本思想是希望通过建立两个总体之间的回归方程，再利用回归方程将一组数据折算到另一组，从而扩大样本容量。

参考产品A的故障数据用X表示，目标产品B的故障数据用Y表示，参考产品与目标产品在可靠性、结构、功能方面相似，且失效机理不变或相似，目标产品通常是在参考产品的基础上改进来的，具有充足的历史数据，因此可将其故障数据作为扩充源。

回归折算法步骤如下：

(1)将样本X和Y的故障数据分别从小到大排列，样本X：x(1)，x(2)，…，x(n)；样本Y：y(1)，y(2)，…，y(m)。

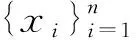
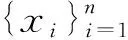
①{x(u),y(v)}作为配对中心保持不变

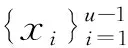
通过最小二乘法[13]估计得到各参数值，建立可靠性模型，并计算出平均故障间隔时间MTBF。

3 Monte-Carlo计算机模拟仿真

通过Monte-Carlo方法对符合威布尔分布模型的数据进行模拟仿真。随机生成大样本数据，应用经典建模法进行可靠性建模，计算出MTBF，以此为基准。从中随机选取一定样本量的随机数作为小样本数据，通过回归折算法对其进行扩充，变成大样本数据后，再用经典建模法建立可靠性模型，计算出MTBF1。对两者的MTBF进行比较，根据其波动性的大小，验证所提方法的有效性和准确性。

具体过程如下：

(1)根上节提到的方法对这些数据进行前期处理，求出x(u)和y(v)以及类的个数l1和l2，并对N1分别进行聚类，并计算每一类的均值，与样本Y构建配对数据；

(2)将以上得到的配对数据进行回归分析，并对回归模型进行优选，得到回归方程；

(3)利用得到的回归方程，对N1个数据进行折算，并与N2个数据组成大样本数据N3；

(4)通过最小二乘法分别对N1和N3个数据进行可靠性建模，并求出MTBF，以N1数据即大样本数据的MTBF为基准，计算误差；

(5)模拟M次，将误差以曲线的形式输出。

以上涉及的参数主要有威布尔分布的尺度参数α，形状参数β，随机数的数量N1和N2以及模拟次数M。尺度参数α和形状参数β是有一定范围的，需根据国内数控机床的实际情况而定。形状参数β代表机床的故障阶段，当0<β<1时，机床处于早期故障时期；β=1时，处于偶然故障时期；β>1时，处于耗损故障时期。由于MTBF=α·Γ(1+1/β)，因此尺度参数α可根据MTBF和形状参数β来确定范围，我国大部分机床专项的数控机床的MTBF一般达到了900h或1500h。现今所研究考核的数控机床多数处于偶然故障时期的附近，根据MTBF的计算公式，即可求出尺度参数α的值。以MTBF=1200h，N1=30，N2=6，M=20的情况下，采取三种模拟方案，①α=1100，β=0.85;②α=1200，β=1;③α=1260，β=1.15，模拟结果如图1所示。

由图1可知，利用回归折算法扩充数据后计算出的MTBF误差在15%左右，在文献[9]中，应用Boostrap-Bayes方法计算出的MTBF与经典建模方法计算出的MTBF的误差在20%以内，利用常规贝叶斯方法计算出的MTBF的误差在30%以内，因此本文模拟出的误差在可接受的范围内，可以得到较为准确的可靠性模型。

4 实例验证

某型号M的同批次7台数控加工中心，分别由Z1,Z2,…,Z7表示，共有60个故障数据，如表1所示。利用经典方法即最小二乘法对M型加工中心的大样本数据进行可靠性模型的建立，并以此为基准。从大样本数据中抽取小样本，来自于Z1,Z2,…,Z7。分别用回归折算扩充数据的方法和经典建模法对小样本数据进行可靠性建模，与基准相比较，对比分析两种方法的误差，以此来验证本文所研究的建模方法的正确性与准确性。

图1 MTBF的误差曲线

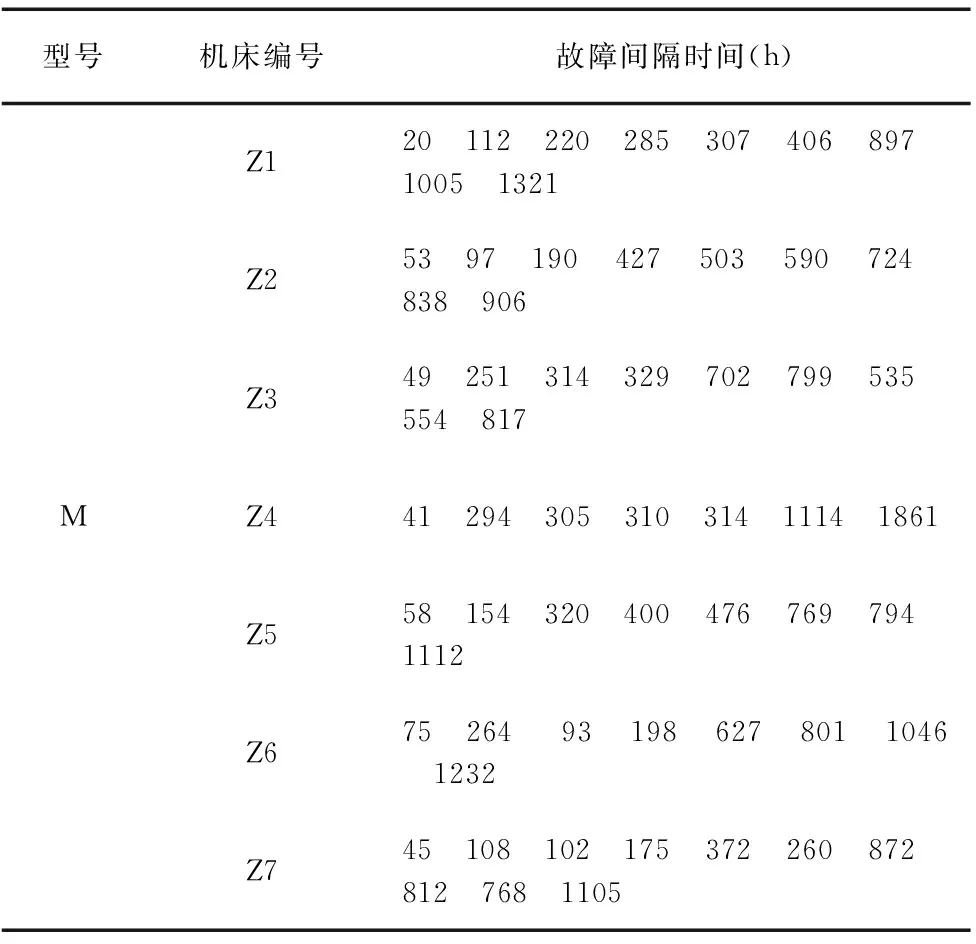
型号机床编号故障间隔时间(h)MZ120 112 220 285 307 406 897 1005 1321Z253 97 190 427 503 590 724 838 906Z349 251 314 329 702 799 535 554 817Z441 294 305 310 314 1114 1861Z558 154 320 400 476 769 794 1112Z675 264 93 198 627 801 1046 1232Z745 108 102 175 372 260 872 812 768 1105

以Z1～Z7加工中心故障数据为大样本数据，利用最小二乘法建立的两参数威布尔分布模型参数如下：α=548.72；β=1.18；MTBF*=518.70h。再分别以Z1,Z2,…,Z7为目标产品，即小样本数据，建立可靠性模型。以Z1为例，根据本文提出的方法，建立配对关系(44.3，20)、(97.8，112)、(187.4，220)、(296.1，285)、(416.2，307)、(503，406)、(753.2，897)、(1133.6，1005)、(1861，1321)，并对以上数据做回归分析。分别选取不同的函数对配对数据拟合，最终确定幂指数函数为最优模型。其回归方程为：

y=3.328x0.8022

(5)

将Z1～Z7的60个故障数据按公式(5)折算，便可得到折算数据，此时Z1加工中心的小样本数据扩充为大样本数据，即可用最小二乘法建立可靠性模型，求得α1=590.61，β1=1.26。因此Z1加工中心的瞬时失效率函数为：

可靠度和瞬时失效率函数的拟合曲线如图2和图3所示。

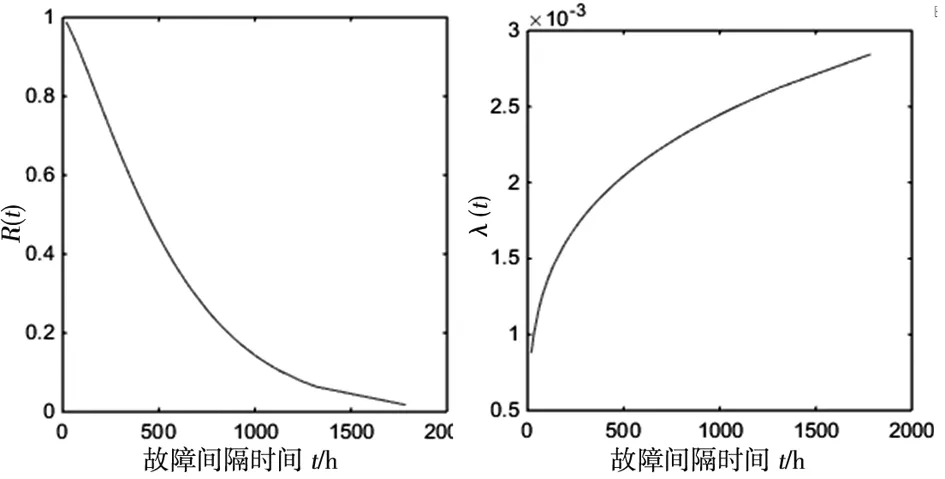
图2 可靠度函数的拟合曲线 图3 瞬时失效率函数的拟合曲线曲线

以加工中心Z2～Z7的小样本数据为基础，分别利用以上的方法和经典建模法建立其可靠性模型参数，其参数估计值如表2所示。

表2 两种方法的可靠性模型参数

将参数估计值分别代入式(6)，计算相应的MTBF，以MTBF*=518.70h为标准，计算两种MTBF的相对误差。

(6)

(7)

计算结果如表3所示。

表3 MTBF的误差

由表3知，利用回归折算方法建立的可靠性模型误差较小，能得到较准确的可靠性模型，验证了本文所提方法的正确性。

5 结论

(1)引入回归折算法对小样本数据进行扩充，能充分利用现存的所有信息，解决了小样本数据量不足的问题。比直接使用传统建模方法建立可靠性模型，其结果更加准确，从而为小样本数控机床的可靠性建模提供了一定的指导方法。

(2)通过Monte-Carlo计算机模拟仿真，可见符合威布尔分布的小样本故障数据经扩充后建立的可靠性模型更加接近真实数据，也证明了回归折算法对威布尔分布模型数据的折算有效。

(3)以加工中心的小样本故障数据为基础，利用回归折算扩充数据的方法和经典建模法分别建立可靠性模型，与以大样本下经典建模方法所建模型进行比较，结果表明本文所提方法建立的可靠性模型误差小。

[参考文献]

[1] Ross R.Bias and standard deviation due to Weibull parameter estimation for small data sets[J].IEEE Transactions on Dielec-trics & Electrical Insulation,1996,3(1): 28-42.

[2] Efron B.Bootstrap Methods:Another Look at the Jackknife[J].The Annuals of Statisti-cs,1979,7(1):1-26.

[3] 钱浩.基于Bootstrap-Bayes的数控机床小子样可靠性建模方法研究[D].长春:吉林大学,2012.

[4] 胡职梁,何雪浤.基于故障信息的数控机床可靠性函数建立[J].组合机床与自动化加工技术,2016(3):97-100.

[5] 游达章,唐小琦,戴怡,等.贝叶斯理论的可靠性评估方法及在数控系统评估中的运用[J]. 中国机械工程,2011,22(3):314-317.

[6] Kan Y，Yang Z,Fei C,et al.Bayesian Reliabi-lity Modeling and Assessment Solution for NC Machine Tools under Small-sample Data [J].Chinese Journal of Mechanical Engineering,2015,28(6):1229-1239.

[7] 张立敏,申桂香,张英芝.小样本数控刀架的可靠性模型[J].吉林大学学报,2012,42(1):96-99.

[8] 高攀东,沈雪瑾,陈晓阳,等.基于自助法的小样本Weibull分布可靠性分析[J].机械设计与研究,2015,31(2)：164-167.

[9] 陈传海,杨兆军,陈菲,等.基于Bootstrap-Bayes的加工中心主轴可靠性建模[J].吉林大学学报：工学版,2014,44(1):95-100.

[10] 孙祝岭.可靠性数据的回归折算方法[J].航天控制,2010,28(3):77-80.

[11] 孙祝岭,白吉潇.可靠性数据的回归折算方法进一步研究[J].质量与可靠性,2010(5):18-21.

[12] Dai Y,Zhou Y F,Jia Y Z.Distribution of time between failures of machining center based on type I censored data[J].Reliabi-lity Engineering & System Safety,2003,79(3):377-379.

[13] 张海波,贾亚洲,周广文.数控系统故障间隔时间分布模型的研究[J].哈尔滨工业大学学报,2005,37(2):198-200.