基于气体发生剂的子弹药气囊抛撒数值模拟研究

王琪， 蒋建伟， 王树有

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

0 引言

子弹药气囊抛撒是子母弹一种常用的抛撒方式，其常见抛撒动力源有火药、推进剂等产气药剂。这类抛撒动力源具有抛撒速度高、产气速度快等优点，但燃烧温度高、抛撒过载大，易造成气囊材料的烧蚀和子弹药结构的破坏。随着子弹药向智能化发展，其内部装载的精密光电设备对抛撒过载提出了更高的要求，因此采用以气体发生剂为动力源的低过载抛撒技术日益受到研究者的重视，尤其是以叠氮化钠(NaN3)为主要成分的气体发生剂,因其燃烧速度适中、燃烧温度低、产气量大等优点正得到愈加广泛的应用[1-2]。

气囊抛撒下子弹药的运动规律研究主要采用理论计算和数值模拟方法，其中理论计算方法包括经典内弹道和两相流理论。经典内弹道理论善于描述抛撒药燃烧过程和燃气的平均状态，但无法精细描述气囊膨胀变形与弹箍断裂等非线性过程，需要对该过程作一定简化。如对抛撒过程中气囊对子弹药的作用面积变化进行一定假设或直接设为定值；忽略弹箍的弹塑性变形，假设弹箍达到断裂强度前不发生形变且子弹药速度为0等[1-6]。这些假设能够简化计算但会带来一定的计算误差。两相流理论则可以较精细地描述内弹道过程，但对三维状况求解较为复杂，不便于实际工程应用[1]。数值模拟方法则主要集中在任意拉格朗日- 欧拉(ALE)法和控制体积(CV)法两种，一般与理论计算或试验相结合，由理论计算或试验提供仿真计算的输入参数。现阶段提出的子弹药气囊抛撒数值模拟方法都具有一定的局限性。如王帅[3]运用经典内弹道理论得到子弹药气囊抛撒各个时期内气囊内部平均压力变化，并将其作为输入参数用CV法进行数值模拟。但CV法定义每一时刻气囊内部各处压力均等，仅适合于分析静态气囊问题及流场影响不大的场合，尚不适合在离位情况下的气囊展开过程的模拟[4]。李嗄[5]通过对比CV法与ALE法，得到了ALE法相对于CV法更适合于子弹药气囊抛撒情况下的数值模拟要求，能精确地模拟燃气冲入状态及气囊外形变化的结论，但所建立的ALE法数值仿真模型假设抛撒药瞬间完全燃烧产生燃气，忽略了抛撒药点火燃烧过程。孟会林等[7]采用ALE法，采用高速爆炸燃烧材料模型和线性多项式状态方程对抛撒药进行定义，但却忽略了燃烧室结构及燃烧室喷孔对药剂燃烧及燃气喷射的影响。

为了获得一种可靠、基于气体发生剂的子弹药气囊抛撒数值模拟研究方法，本文在气体发生器内弹道试验基础上，使用名义燃速方程描述气体发生器组件的整体燃烧特性,将内弹道计算得到的燃气质量流率随时间变化曲线作为数值模拟计算的输入参数来模拟燃气充入过程，提出了一种计算简便、实用性强的子弹药气囊抛撒ALE数值仿真计算方法。

1 气体发生剂囊抛子弹药数值仿真

1.1 物理模型

图1是典型气体发生剂的子弹药气囊对称抛撒装置结构示意图[1-2]，该抛撒装置包括弹箍、气体发生器、气囊、蒙皮、气室、子弹药等部分。其工作原理是：气体发生剂点火燃烧产生燃气，燃气经过气体发生器内部燃烧室升压、金属箔破裂、滤网过滤等过程后从气体发生器喷孔中冲出，进入气室和气囊，造成气囊与气室内部压力升高，气囊变形膨胀。随后气囊对子弹药产生压力作用，推动子弹药发生运动并使弹箍发生弹塑性变形，当弹箍变形达到一定程度时，弹箍在其中部薄弱处断裂，子弹药解除约束，内部喷射燃气能量通过气囊迅速释放，最终将子弹药抛射出去。

1.2 有限元模型建立

采用网格划分Truegrid软件对有限元模型进行参数化网格建模，因抛撒装置呈双向对称抛撒，故建立二分之一的三维有限元模型，其中气囊、气室和弹箍为Shell163壳单元，其余部件为Solid164实体单元，外界空气和内部喷射燃气采用多物质ALE算法，其余部件为拉格朗日算法。图2为建立的子弹药气囊抛撒三维有限元模型，子弹药简化为空心圆柱体，外径80 mm，内径70 mm，长度400 mm，总质量3.75 kg. 外部空气域尺寸为460 mm×370 mm×140 mm，气室尺寸为400 mm×50 mm×33 mm,气囊尺寸为400 mm×160 mm×10 mm. 采用前后处理Ls-PrePost软件的ABFold模块，按照折叠线和折叠流程，通过平面折叠方式中的thin fold折叠方法对气囊进行折叠[8]。

1.3 材料参数选取

气囊材料采用*MAT_FABRIC定义，外界空气、喷射燃气材料特性和初始化使用关键字*MAT-GAS- MIXTURE与*INITIAL-GAS- MIXTURE实现[9]。内部喷射燃气无初始网格，随着喷射过程逐渐占据空气网格区域。

喷射气体状态采用*SECTION_POINT_SOURC E_MIXTURE关键字设置，在该关键字下定义喷射气体的质量流率随时间变化曲线及气体喷射点、喷射方向等参数[9]。采用内弹道计算给定的质量流率随时间变化曲线(第2节详细阐述)作为有限元模型内部喷射燃气的喷射状态参数输入。沿气体发生器轴线方向均匀设置数个节点为气体喷射点，气体喷射方向与子弹药运动方向相同。表1为各部件材料模型及状态方程，表2列出了气囊织物密度与材料各方向的杨氏模量、剪切模量和泊松比参数。

表1 子弹药气囊抛撒数值模拟材料关键字表

表2 气囊织物材料参数[10]

1.4 边界条件与接触设置

在外部空气域边界施加无反射边界条件，由于弹箍在装配过程中束缚并压紧子弹药，故在有限元模型建模中使弹箍与子弹药紧贴，并在弹箍两侧施加固定约束条件以模拟真实情况。

气囊自身接触用*CONTACT_AIRBAG_SINGL E_SURFACE关键字定义，气囊与其他部件间的接触用关键字*CONTACT_AUTOMATIC_SURFACE_TO _SURFACE来定义，采用面面接触能保证气囊与子弹药一直相互接触紧贴，不会发生无规则震荡现象。

修改气囊与气室壳单元法向方向，使其全部指向气囊及气室内部，以使拉格朗日单元与流体单元能够进行流体与固体耦合。

2 名义燃速方程及质量流率参数获取

2.1 内弹道基本假设

气体发生器通常带有燃烧室和低压室两个气室，可将其视作整体，建立气体发生器整体燃烧特性和外界压力的关系，称为名义燃速方程[1-2,11]，其形式可表示为

r=apb+c，

(1)

式中：r为名义燃速(m/s)；p为气体发生剂燃烧过程中的环境压力(MPa)；a、b、c为与气体发生剂种类和药形、气体发生器内外燃烧室容积、气孔面积等结构尺寸有关的参数。因此在气体发生剂种类和药形、气体发生器结构尺寸不变的条件下名义燃速方程不变。图3为采用密闭爆发器测定名义燃速方程的试验装置示意图。

采用密闭爆发器试验测定名义燃速方程的内弹道过程[1-2,12]可由(2)式描述：

(2)

式中：ψ为相对已燃量；χ、λ、μ为燃气生成系数；Z为相对已燃厚度；δ1为药粒厚度；δ为燃烧厚度；γ为气体发生剂的密度；α为燃气余容；f为气体发生剂火药力；ω为装药量；V0为密闭爆发器容积。

2.2 名义燃速方程的拟合

为对药剂的名义燃速方程参数a、b、c进行确定，对装有不同氮气发生剂装药量的气体发生器进行密闭爆发器试验，试验装置如图4所示。图5为在密闭爆发器内放置压力传感器所测得的典型氮气发生剂药量(80 g，120 g)下的p-t曲线。

试验中所使用氮气发生剂药形为圆筒状，其内外径为2Ri和2Ro，厚度为2δ1，则其燃气生成函数为

(3)

使用外推法对不同药量下密闭爆发器中最大压力pm进行热散失修正[12]，代入(4)式、(5)式得到该型氮气发生剂的火药力f=451 702 J/kg、余容α=0.003 62 m3/kg.

(4)

(5)

将80 g药量条件下的p-t试验数据代入(2)式，编制MATLAB程序，得到试验条件下名义燃速r随密闭爆发器内压力p变化曲线，最小二乘法拟合得到名义燃速方程为

r=0.017 4p0.712.

(6)

为了验证所得到的名义燃速方程及名义燃速假设的正确性，将燃速方程(6)式代入(2)式，使用4阶龙格- 库塔法解出另一药量下的p-t曲线，图6为120 g药量下试验和理论计算所得p-t曲线，二者吻合较好，证明名义燃速假设正确且所求得的名义燃速方程可以表征本气体发生器的整体燃烧特性。此时(2)式为闭合方程组，可以解出该型药剂不同药量及密闭爆发器容积下密闭爆发器内的p-t变化。

2.3 氮气发生剂质量流量的求解

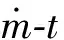
(7)

3 数值仿真结果与分析

3.1 药量对子弹药运动参数的影响分析

根据建立的有限元模型，采用LS-DYNA软件对不同氮气发生剂药量下子弹药气囊抛撒规律进行数值模拟。图7、图8为装有80 g气体发生剂的子弹药气囊抛撒过程和内部燃气喷射状态(以80 g药量为例)，图9、图10为不同药量下子弹速度- 时间、加速度- 时间历程曲线。弹箍所采用的削弱方式为削弱槽削弱，图11显示了弹箍的断裂状态。

数值模拟结果表明，子弹药出舱速度v和过载峰值a随着氮气发生剂药量增加而增加，而抛撒时间则随药量增大而缩短，达到过载峰值的时刻随药量增大而变快。40 g、80 g、120 g、160 g药量下弹箍断裂时刻分别为7.5 ms、6.5 ms、5.0 ms、4.5 ms，对比图10各曲线可以观察到，弹箍断裂时刻与子弹药加速度发生较为明显变化的时刻相对应，弹箍断裂后子弹药加速度增长率得到明显提高。随着药量增加，抛撒过程中内部燃气的最大压力值也随之增加，分别为1.6 MPa、2.5 MPa、3.6 MPa、4.8 MPa.

图12、图13为不同药量下采用最小二乘法拟合得到的子弹药出舱速度、过载峰值随药量的变化，可得子弹药出舱速度和过载峰值与药量(g)之间的关系为

v=14.38+0.133ω,

(8)

a=1 901+44.616ω.

(9)

3.2 弹箍因素对子弹药运动参数的影响分析

弹箍除了在装配过程中起到约束子弹药的作用，其存在本身也对子弹药抛撒过程产生影响。为分析其影响，针对不同药量下有无弹箍的抛撒工况进行数值模拟，得到子弹药出舱速度、过载峰值随各工况变化，如图14、图15所示。

由图14、图15数值模拟结果表明，在相同药量下带弹箍工况的子弹药出舱速度和过载峰值大于无弹箍工况下的子弹药出舱速度和过载峰值，这是由于弹箍的存在会限制抛撒初期的子弹药运动，导致同时刻气囊容积较小，气囊内部压力增大，故当弹箍断开后，子弹药所受过载将大于无弹箍工况，提高了有弹箍工况下的子弹药抛撒速度。因此加装弹箍不仅为约束和固定子弹药，也能起到提高子弹药出舱速度的作用。

4 试验验证

为了验证子弹药气囊抛撒数值模拟结果的正确性，设计了与仿真模型完全一致的子弹药气囊对称抛撒装置。图16为子弹药气囊对称抛撒装置图(装填80 g氮气发生剂，加装弹箍)，在子弹药外壁安装压电式加速度传感器以记录子弹药过载，采用高速摄影机拍摄子弹出舱速度。图17为抛撒试验布置图，图18为80 g药量下子弹药气囊抛撒过载数值模拟与试验结果对比。

在抛撒试验中，实测和数值模拟计算子弹药过载峰值分别为592g和569g,二者误差4%；实测和数值模拟计算子弹药出舱速度分别24.6 m/s和26.3 m/s，二者误差7%. 数值模拟与实验结果基本吻合，证明子弹药气囊抛撒数值仿真方法正确，且具有工程指导意义。

5 结论

1)在气体发生器内弹道理论与试验研究基础上，结合内弹道编程，拟合得到某型氮气发生器的名义燃速方程。通过对比不同药量下密闭爆发器内p-t曲线的试验与理论计算结果，表明使用名义燃速方程描述气体发生器燃气的释放规律是可行的。

2)根据气体发生剂反应的内弹道模型，得到燃气的质量流率随时间曲线的求解方法。采用LS-DYNA有限元软件，建立以燃气质量流率- 时间历程曲线为输入条件的子弹药气囊抛撒ALE流体与固体耦合计算模型，通过数值模拟得到本抛撒结构下子弹药出舱速度及过载峰值随药量变化规律，得到各抛撒药量下弹箍断裂时刻及内部燃气最大压力的变化，同时验证了弹箍对子弹药抛撒的促进作用。

3)对数值模拟计算结果进行子弹药气囊抛撒试验验证，80 g药量带弹箍工况下子弹药出舱速度计算误差为7%，过载峰值计算误差为4%，证明所得数值模拟结论可信，本数值计算方法可用于抛撒技术研究和工程应用。

参考文献(References)

[1] 房玉军.子母弹气囊抛撒技术的理论与实验研究[D].北京:北京理工大学，2005.

FANG Yu-jun.Theory and experimental research on submunition dispenser with airbag[D].Beijing:Beijing Institute of Technology,2005. (in Chinese)

[2] 蒋建伟,房玉军,门建兵,等.采用氮气发生剂的子弹药气囊抛撒内弹道计算模型[J].北京理工大学学报，2006,27(5):883-886.

JIANG Jian-wei,FANG Yu-jun,MEN Jian-bing,et al.Interior ballistic model of submunition dispenser with nitrogen gas generant and airbag[J]. Transactions of Beijing Institute of Technology, 2006,27(5):883-886.(in Chinese)

[3] 王帅.子母战斗部囊式抛撒系统实验研究及数值仿真[D].南京:南京理工大学,2013.

WANG Shuai.Experimental and simulation study on the explosive cluster warhead dispersion system[D]. Nanjing:Nanjing University of Science and Technology,2013.(in Chinese)

[4] 余莉，程涵，刘雄.气囊充气过程流固耦合数值模拟[J].南京航空航天大学学报，2010,42(4):472-476.

YU Li,CHENG Han,LIU Xiong.Numerical simulation of airbag during deploying process[J].Journal of Nanjing University of Aeronautics and Astronautics,2010,42(4):472-476. (in Chinese)

[5] 李嗄.气囊式子母弹抛撒过程数值模拟[D].南京:南京理工大学,2012.

LI A.Numerical simulation on dispersal process of gasbag-style cluster bombs[D]. Nanjing:Nanjing University of Science and Technology,2012. (in Chinese)

[6] 王浩.子母弹内燃式气囊抛撒模型及计算机仿真[J].兵工学报,2001,22(2):178-181.

WANG Hao.A model for the firing process of the internal-combustion gasbag submunition and its simulation[J]. Acta Armamentarii, 2001,22(2):178-181. (in Chinese)

[7] 孟会林,孙新利,姬国勋,等.子母弹抛撒过程数值模拟及其试验[J].弹箭与制导学报,2004,24(8):317-321.

MENG Hui-lin,SUN Xin-li,JI Guo-xun,et al. Test and numerical simulation of the bullets spreading process of a primary-secondary bomb[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(8):317-321. (in Chinese)

[8] 张翔.子弹药低过载气囊驱动技术研究[D].北京:北京理工大学,2016.

ZHANG Xiang.Research on technology of low overload airbag driving submunition[D]. Beijing: Beijing Institute of Technology,2016.(in Chinese)

[9] 代小芳.基于流固耦合方法的气囊展开数值模拟研究[D].大连:大连理工大学,2008.

DAI Xiao-fang.Numerical simulation of airbag deployment based on fluid-structure interaction methodology[D].Dalian:Dalian University of Technology,2008. (in Chinese)

[10] 王帅,王浩,李嗄.含芳纶织物增强内衬复合材料气囊的静态变形过程实验研究与数值模拟[J].功能材料,2013,44(14):2097-2010.

WANG Shuai, WANG Hao, LI A. Experimental research and numerical simulation on static deformation of gasbag with textile reinforced composite lining[J]. Journal of Functional Materials, 2013,44(14):2097-2010. (in Chinese)

[11] Hyun J K,Chang S K,Jun S H. A study of gas generator with double nozzle system[C]∥28th International Annual Conference of ICT. Karlsruhe,Germany: ICT, 1997:125-1-125-12.

[12] 鲍廷钰,邱文坚.内弹道学[M].北京:北京理工大学出版社,1992.

BAO Ting-yu, QIU Wen-jian. Theory of interior ballistics[M]. Beijing:Beijing Institute of Technology Press, 1992. (in Chinese)

[13] 朱跃龙.底火能量释放特性及其对内弹道性能研究的影响[D].南京:南京理工大学,2014.

ZHU Yue-long. The primer energy release characteristics and its influence on the interior ballistic performance[D]. Nanjing: Nanjing University of Science and Technology,2014.(in Chinese)