表面凹凸药形固液火箭发动机燃速特性仿真研究*
2021-02-16魏小青李悦龙
魏小青,李悦龙 ,杨 乾
(中国航天科技集团有限公司四院四十一所,西安 710025)
0 引言
固液火箭发动机是一项发展迅速的推进技术[1-2],与传统的液体火箭发动机和固体火箭发动机相比,具有安全、低成本、无污染和推力易调节等优势。所以,被应用于低成本的靶标与导弹、探空火箭与小型运载火箭、以及亚轨道飞行器与载人飞船等领域。但是其固有的低燃烧速率、低燃烧效率和低装填率却阻碍了其推广运用。因此,如何提高固液火箭发动机燃速成为发动机燃烧过程研究中的一个热点,国内外都有大量的关于用不同方法提高固液火箭发动机燃速的研究[3-4]。
通过采用新组分燃料药柱来提高燃速,如冷冻型固体燃料、石蜡或者向固体燃料药柱中添加高能金属颗粒(如Na、Al)及高能氧化剂AP等。通过添加高能金属颗粒,可以提高固体燃料分解产物与氧化剂的反应放热,降低固体燃料气化分解所需要的气化热,从而提高燃速[5]。虽然新组分燃料药柱能有效提高燃料的燃速,但其也有局限性。冷冻型燃料难于储存,添加高能颗粒又降低了发动机安全性。所以,运用受到一定限制。
采用氧化剂旋转喷注方式。固液火箭发动机燃料燃速不高的根本原因是固体燃料和气态氧化剂之间的扩散燃烧过于缓慢。随着近些年对燃烧机理的深入研究,YUASA等[6]、BELLOMO等[7]、OHYAMA等[8]发现氧化剂旋转喷注可有效增强火焰层与燃料壁面的热量传递,同时延长燃烧的有效时间,进而大大提高燃料的燃速和燃烧效率。虽然氧化剂旋转喷注可以大大提高燃料的燃烧速率,但燃速的增强效应更多地局限在药柱入口端,而且由于气体膨胀、粘性损失以及来自药柱表面燃料热解气体的释放(吹风效应)等原因,会使得通过旋转喷注器喷入的螺旋流场沿轴向迅速衰退,进而导致燃料燃速沿轴线分布不太均匀。为了克服这些问题,同时更进一步提升燃速,一些新型药形被提出,比如KIM J等[9]提出锥型药形、HATAGAKI等[10]提出表面凹凸药形、ARNOLD等[11]、LEE等[12-13]、TIAN Hui等[14]提出螺旋药形,以期通过对燃气流动的扰动,增强燃气与固体燃料壁面的对流换热,从而增强燃速。
本文基于以上背景,通过建立纯气相反应模型,对GOX/HDPE推进剂组合的表面凹凸药形固液火箭发动机进行数值模拟,得到内流场的燃烧、流动特性,对比不同槽间距、槽深以及氧化剂流量组合的工况,分析不同工况燃速的变化规律。
1 数值仿真模型
固液火箭发动机的工作过程包括氧化剂喷注、固体燃料热解、燃面退移、气相组分燃烧、湍流流动等,多个过程的耦合使得其实际流动燃烧过程相当复杂。为更好开展固液发动机数值仿真工作,需要把握其中的主要问题,对复杂的物理化学现象做一定的假设:
(1)假设发动机稳定工作,其燃烧流动状态为准定常。由于固液发动机燃速较小,所以不考虑燃面退移引起的计算域的变化。
(2)不考虑喷注雾化过程。由于采用气氧作为氧化剂,故本文将燃烧室内的流动视为纯气相流动。
(3)不考虑凝相、热辐射等作用,燃烧产物中气相组分皆按理想气体状态方程处理。
本文的数值仿真工作基于FLUENT软件进行,其中气相模型、湍流模型、化学反应模型通过软件直接设置,燃料热解模型和气固耦合模型通过UDF(User Defined Functions)以源项的形式添加。
1.1 气相和湍流模型
气相控制方程采用N-S方程与湍流模型方程和燃烧组分输运方程相耦合的方式:
(1)
(2)
(3)
(4)
式中ρ为气体密度;Ym为第m种组分的质量分数;τij为粘性应力张量;H为UDF等引起的相应源项。
湍流模型采用Realizablek-ε模型,该方程由k方程和ε方程组成,适于求解包括旋转均匀剪切流、管内流动、边界层流动的流动状态。
1.2 化学反应模型
文中采用HDPE作为固体燃料药柱,纯GOX作为氧化剂的推进剂组合。其中HDPE主要分解产物为乙烯(C2H4),计算过程中不考虑其他的热解产物,采用C2H4和O2的一步多产物反应:
2C2H4+4O2→3CO+CO2+H2O+2H2+2OH
(5)
化学反应速率采用涡耗散模型(Eddy Dissipation Model,EDM)。
1.3 气固耦合模型
固液火箭发动机的燃烧特点是中心区氧化剂来流与固体燃料热解产物在附面层中相遇,形成火焰层,在火焰层中反应燃烧。其中,固体药面的热解速率与药面温度有很大关系,可以用Arrhenius(阿累尼乌斯)公式描述:
(6)
式中A为指前因子;E为活化能;Ts为固体燃料表面温度。
在靠近固体燃料壁面附近,流体与固体之间的作用主要通过质量守恒和能量守恒两个关系描述,其中质量守恒方程:
ρgv=-ρsr
(7)
式中ρg为固体燃料热解气体密度;v为壁面外法线方向速度;ρs为固体燃料的密度;负号表示v与r的速度相反。
能量守恒方程:
(8)
式中hg为气相分解产物在热解温度下的焓值;hs为固体燃料在热解温度下的焓值。
实际仿真计算中,通过对式(6)~式(8)进行迭代计算,最终求得燃速和固体燃料表面温度,然后把固体燃料质量、动量和能量以源项的形式加入到网格中去,其源项的具体形式如下:
SΦ=ρsrΦAc/Vc
(9)
式中 Φ为任一标量;Ac为固体药柱表面网格单元面积;Vc为与药柱表面相连的、网格单元体积。
2 计算模型
2.1 几何模型和网格化分
仿真计算基于试验规模的发动机进行几何建模,发动机直径为100 mm,其结构如图1所示。氧化剂入口直径为36 mm,药柱内径为40 mm,药柱长度为375 mm,喷管喉径为15 mm。为更清晰地显示凹凸槽对药柱燃烧带来的影响,只在药柱后半段添加凹凸槽,前半段依然为直管药形。其中,A为槽间距,B为槽深、C为槽宽。
数值计算以Fluent软件为平台展开,氧化剂入口边界条件设为质量流量进口边界条件,温度298.16 K;药柱壁面设置为流-固界面,通过写有流-固耦合方程的UDF程序向Fluent软件中添加相应源项来模拟固体燃料药柱的燃烧;其他固体表面设置为绝热边界(Adiabatic,no-slip);出口边界为压力出口边界条件,设置为0.1 MPa;轴线则设为对称边界条件。
表面凹凸形药柱结构关于中心轴线对称,仿真计算所用网格见图2。固体燃料表面温度及温度梯度对其燃速有很大影响,所以对药柱表面附近计算域的网格进行加密处理。第一层网格取0.01 mm,加密网格层数为10层,同时用y+(y+=Δyρuτ/μ)来衡量湍流模型中对壁面网格求解粘性底层的精度,其中要求y+满足数量级为1的要求。
2.2 算例验证
为验证计算模型的合理性和正确性,本为针对文献[15]中的S1PE固液火箭发动机的实验数据进行验证。该S1PE固液火箭发动机采用纯氧气作为氧化剂,内孔PE药柱作为固体燃料。图3为采用本文仿真模型得到的燃速和文献[15]中的试验得到燃速对比。
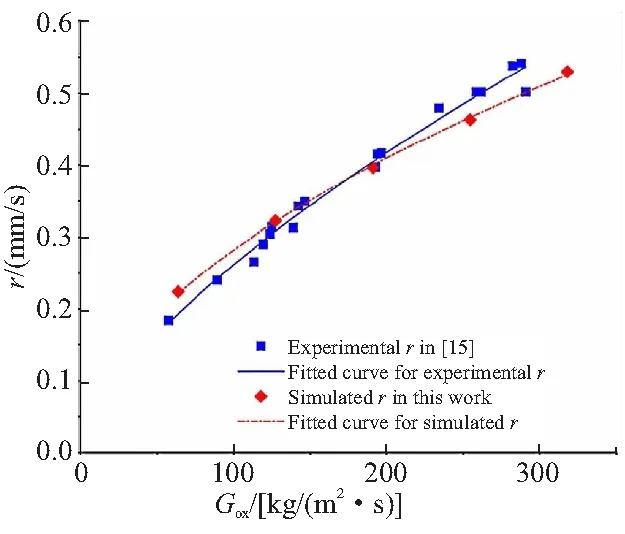
图3 计算结果与实验结果对比
由图3可见,计算结果与试验结果吻合较好,燃速随着氧气流量的增加而变大。通过算例与试验的对比分析,该数值模型可以较好地模拟固液火箭发动机试验,并预示固体药柱的燃速。
3 仿真结果分析
为研究表面凹凸药形的燃速特性,本文分别对不同氧化剂流量、不同槽间距、不同槽深等因素进行数值仿真,仿真选用气氧(GOX)/高密度聚乙烯(HDPE)的推进剂组合,设计氧燃比O/F介于5~15之间,根据选取的药柱模型尺寸,选取氧化剂流量分别为100、150、300 g/s。具体仿真变量值如表1所示。
仿真计算中所有工况燃速r均由对固体燃料壁面燃速进行面积加权平均获得。仿真结果见表2。其中B1、B2和B3为氧化剂流量分别为100、150、300 g/s的直管对照组。

表1 仿真变量值
3.1 氧化剂流量对燃速的影响
为探究不同氧化剂流量对表面凹凸药形燃速的影响,将仿真数据根据不同的槽间距分为3类。图4分别是槽间距为18 mm、槽间距为30 mm、槽间距为60 mm时,不同结构药形燃速随氧化剂流量的变化。
由图4可见,对于几何尺寸相同的凹凸形药柱,药柱的燃速随着氧化剂流量的增加不断增大,且槽深为6 mm时的燃速是同组工况中最低的。对于槽深为4 mm的工况,当气氧流量为100 g/s和150 g/s时,凹凸形药柱的燃速通常大于相同氧化剂流量下直管形药柱燃速;即随着氧化剂流量的增加,药柱整体平均燃速有所增加,但氧化剂流量越大,凹凸药型的作用越不明显。当氧化剂流量增大到300 g/s时,凹凸形药柱的燃速基本小于直管形药柱。下文将对流场进行分析,来探究形成这一规律的原因。
图5为T4和T30两个工况的平面温度云图。从云图中可知,添加凹凸槽后,火焰层向中心轴线偏离,且氧化剂流量越小,偏离越严重。分析认为,这是由于凹槽内固体燃料热解气化,生成的气态燃料向外流动,将火焰层推离药柱壁面导致。
图6为T4和T30局部药柱壁面温度/燃速的对比图。从图6中可以看出,表面凹凸形药柱凸表面的燃速比相同氧化剂流量工况下直管药柱燃速都高(相同位置);一般情况下,凹表面燃速则比相同氧化剂流量工况下直管药柱燃速要低(相同位置)。主要是由于燃气对凸表面前端的冲击,使得凸表面前端燃速急剧增加,紧接着燃速随着火焰层的流动发展先减小后又逐渐增加,这类似于直管药柱燃速沿轴向的变化规律。正由于该扰动的存在,使得凹凸形药柱凸面的燃速比相同氧化剂流量、相同位置处直管药柱的燃速要高,这是凹凸形药柱局部燃速较高的根本原因。
进一步分析认为,对于几何尺寸相同的凹凸形药柱而言,当氧化剂流量较小时,由于凹槽内壁面的燃速与同等工况下直管药柱壁面燃速相差不多,此时凹槽的存在对整体药柱燃速的降低作用不太明显,此时药柱平均燃速主要由凸表面燃速决定。当氧化剂流量较大时,凹槽内药柱壁面的燃速大大低于相同位置处直管药柱的燃速,使得平均后的整段药柱的燃速增加幅度大大降低,此时药柱平均燃速主要由凹槽燃速决定。
综上,凹凸药形药柱平均燃速是凸表面正激励和凹槽负激励相互平衡的结果,不同氧化剂流量条件下,由于正负激励所占的比重不同,导致了如上规律。
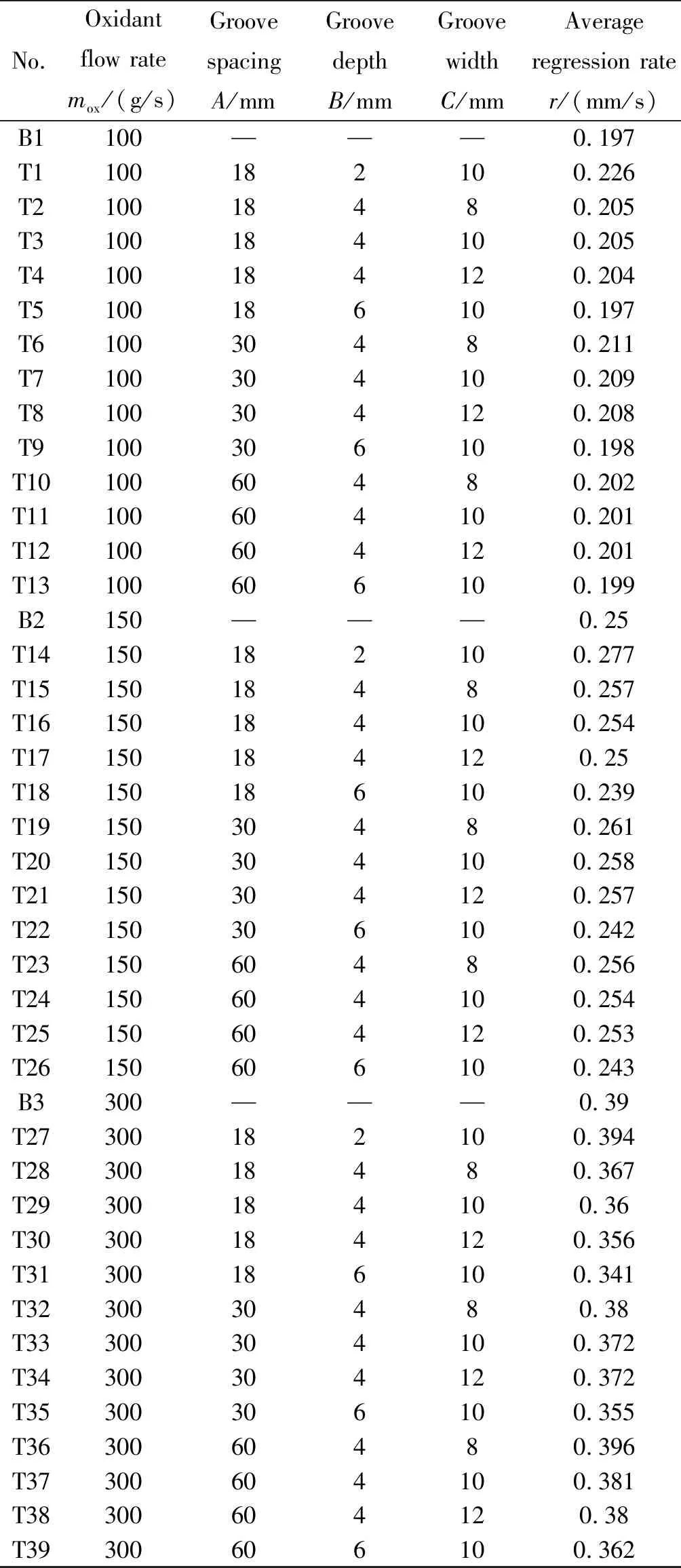
表2 仿真结果
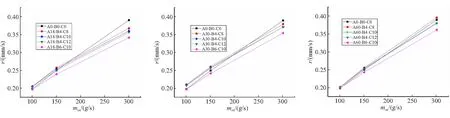
(a) A=18 mm (b) A=30 mm (c) A=60 mm

(a) Temperature contours of localized T4 plane (b) Temperature contours of localized T30 plane
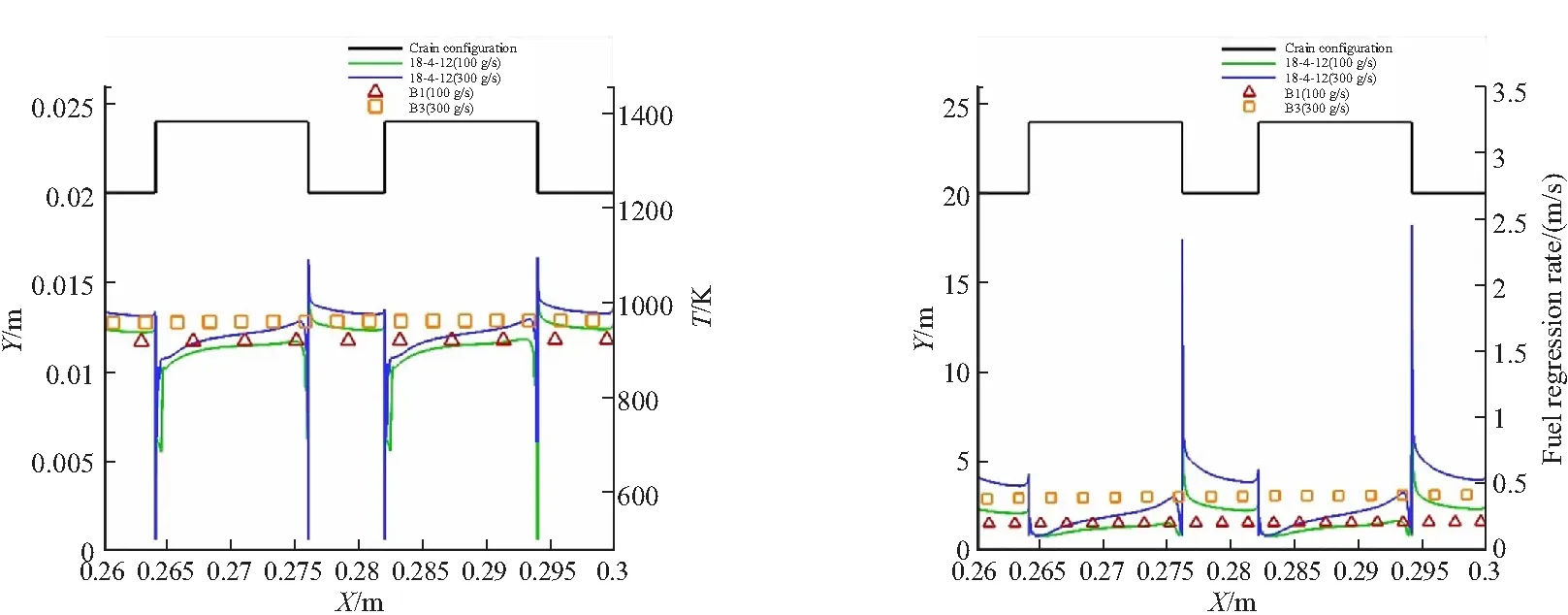
(a) Surface temperature of localized grain (b) Regression rate of localized grain
3.2 槽间距及槽宽对燃速的影响
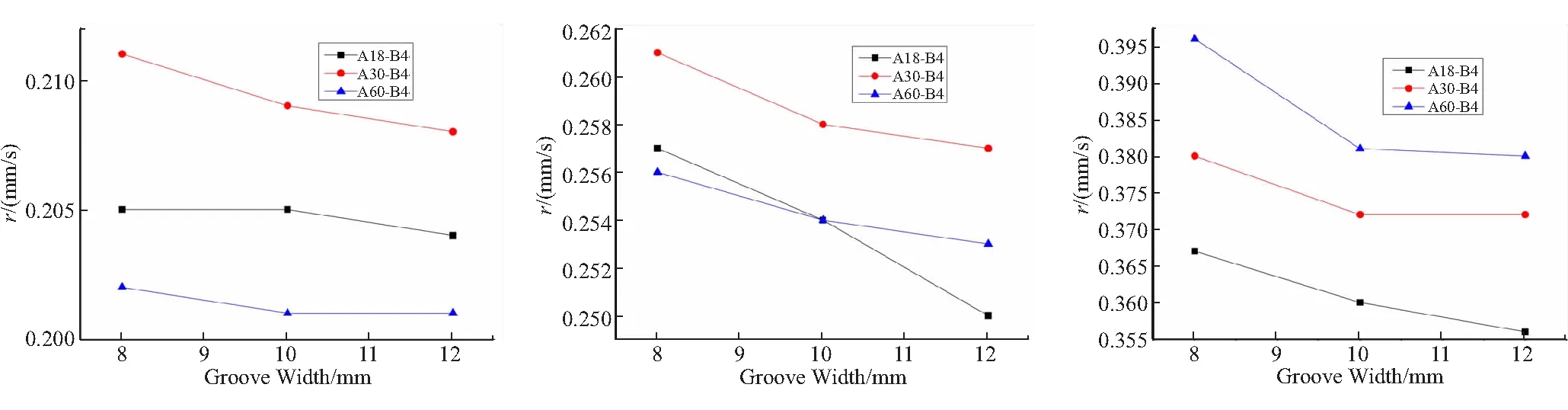
图7分别是氧化剂流量为100、150、300 g/s时,药柱燃速随槽间距的变化。结合表2可以看出,当氧化剂流量为100、150 g/s时,凹凸药柱的燃速高于直管形药柱,随着槽间距的增加,药柱平均燃速先增加后减小,燃速不断逼近直管药柱平均燃速;当氧化剂流量增加到300 g/s时,随着槽间距增加,药柱平均燃速亦增加,燃速不断逼近直管药柱。
图8分别是氧化剂流量为100、150、300 g/s,药柱燃速随槽宽的变化。从图8中可以看出,随着槽宽的增加,药柱的平均燃速不断减小。
图9~图11分别为T4、T21、T38在氧化剂流量为100 g/s时与直管药形B1的药柱壁面温度及燃速的对比图。从图9~图11中可以看出,表面凹凸形药柱凸表面的燃速比凹表面(槽内)的燃速和相同氧化剂流量工况下直管药柱燃速都高;凹表面燃速则比相同氧化剂流量工况下直管药柱燃速要低。

(a) mox=100 g/s (b) mox=150 g/s (c) mox=300 g/s
(a) mox=100 g/s (b) mox=150 g/s (c) mox=300 g/s
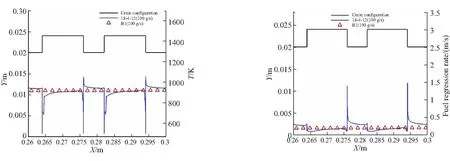
(a) Surface temperature of localized grain (b) Regression rate of localized grain
进一步的分析认为,在一个波动周期内,燃气首先进入凹槽,随后在凸表面产生一次扰动后火焰层不断恢复发展,此过程中燃速逐渐降低,不断逼近相同位置直管药柱燃速。所以,一个波动周期内药柱燃速整体呈现出先降低后增加,最后再降低的发展趋势。
在氧化剂流量较小时,对于一定槽间距(槽宽固定)范围内的凹凸药柱,随着槽间距增加,在经历凸表面后燃速恢复发展越久,越有益于整体平均燃速增加;当槽间距增加到一定值后,随着槽间距继续增大,凸表面对燃速的扰动减少,即对整体平均燃速的正激励减少,凹槽对整体平均燃速的负激励增加,使得药柱平均燃速降低,逐渐逼近于相同氧化剂流量条件下直管药柱的平均燃速。
氧化剂流量较大时,凹凸药柱平均燃速通常低于相同条件下直管药柱平均燃速。此时,凹槽对平均燃速的影响占主导作用。因此,随着槽间距增加,凹槽个数减少,平均燃速增加,并逐渐逼近于相同氧化剂流量条件下直管药柱的平均燃速。
当槽宽较大时(槽间距固定),凹槽内燃速值在整个药柱平均燃速中占有较大比重,导致整体燃速偏低。因此,在其他条件相同情况下,随着槽宽增加,凹凸药型平均燃速降低。
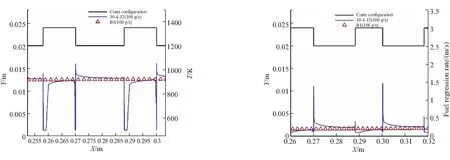
(a) Surface temperature of localized grain (b) Regression rate of localized grain
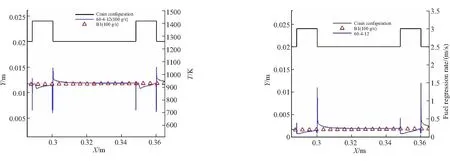
(a) Surface temperature of localized grain (b) Regression rate of localized grain
3.3 槽深对燃速的影响
图12 是氧化剂流量为100、150、300 g/s时,槽间距为18 mm、槽宽为10 mm的药形燃速随槽深的变化。可以看出,槽深对燃速的影响较大,且燃速基本上随槽深增加而降低。
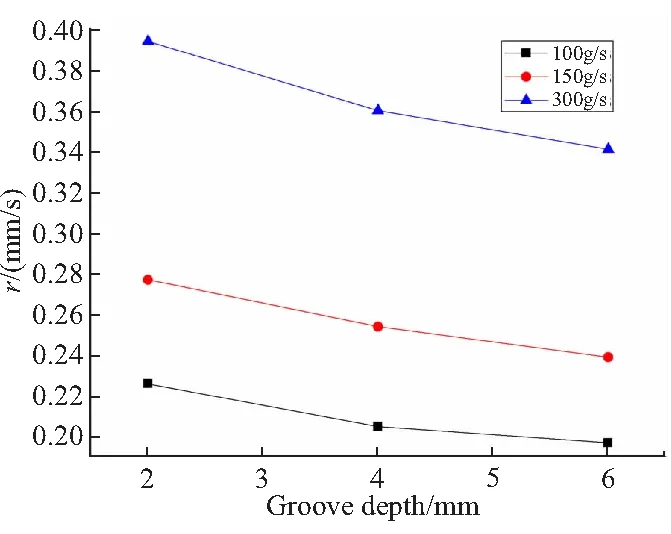
图12 不同流量下燃速随槽深的变化图
图13展示了在氧化剂流量为150 g/s,槽间距为18 mm、槽宽为10 mm、槽深分别为2、4、6 mm三种工况局部壁面温度和燃速的对比图。由图13可知,不同槽深药形药柱壁面温度和燃速差别主要在凹槽内。三个工况凸起部分药柱表面温度和燃速基本一致,但随着槽深增加,凹槽内药柱壁面温度降低,燃速也降低;虽然凹槽后段壁面温度和燃速有所增加,但都小于直管形药柱相同轴向位置处壁面温度和燃速。由此可知,凹槽越深,槽内燃速越低,这是导致药柱整体平均燃速降低的原因。
图14为槽深分别为2、6 mm的温度云图。图15为槽深为2、6 mm的流线图。从图14和图15中可以看出,槽深较浅的药柱,火焰层更容易进入槽内,即高温燃气更容易将热量传递到凹槽内药柱壁面;而较槽深较大的药柱,槽内形成了一个“避风港”,槽内流动和传热相对平缓。
(a) Surface temperature of localized grain (b) Regression rate of localized grain
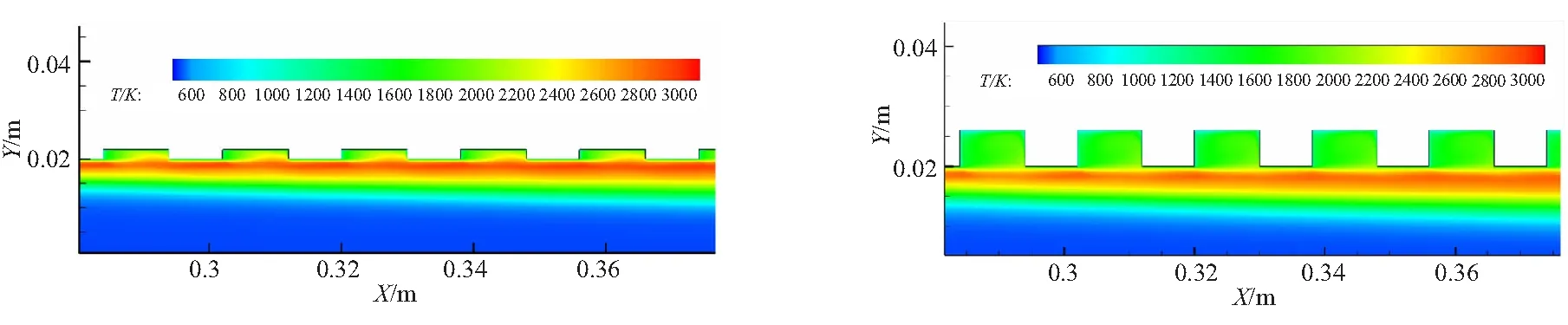
(a) Temperature contours of grain with 2 mm groove depth (b) Temperature contours of grain with 6 mm groove depth

(a) Streamlines of the grain with 2 mm groove depth (b) Streamlines of the grain with 6 mm groove depth
图16为不同槽深药形在不同轴向位置处,温度沿径向的分布情况。由图16可见,槽深越深,温度梯度越小,热量由火焰层向槽内药柱壁面的传递也越困难。当槽内产生涡流时,使得燃气混合更均匀,槽内温度也趋于均匀。从图15可知,对于大槽深结构来说,整体的大涡流占据了槽内大部分空间,这导致温度曲线上出现了平行段,说明涡流使得该空间内温度趋于一致,没有了温度梯度,使热传导更加困难。对于小槽深结构则不一样,虽然凹槽前端同样出现平行直线段,但直线段较短,且到凹槽后半段由于涡流强度减弱,部分高温燃气能够流到凹槽内部,使得平行直线段迅速消失,温度梯度越来越大,对流换热增强,槽内药柱壁面燃速增加。所以,燃速基本上随槽深增加而降低。
4 结论
文中对不同槽间距、槽深、槽宽和氧化剂流量工况的表面凹凸形药柱进行了二维仿真,得到不同工况药形的温度分布、燃烧特性及燃速规律:
(1)通过对凹槽内局部温度、燃速的分析发现,凹凸槽凸起部分受到来流冲刷作用,导致氧化剂流速减小,氧化剂与燃料充分反应,进而使燃速增加。
(2)氧化剂流量增加,表面凹凸形药柱燃速增加,但增加幅度随流量增加逐渐减小。
(3)槽间距增加,表面凹凸形药柱的平均燃速通常先增加,但最终逼近相同氧化剂流量条件下直管药柱平均燃速;槽宽增加,平均燃速降低。
(4)槽深对燃速影响较大,槽深越深,火焰层高温燃气向槽底燃面的热量传递越困难。所以,槽底燃速越低,药柱平均燃速越低。
(5)凹凸槽方案在工作初期可以有效提高燃速,但是凸出部分燃速过高,凹槽部分燃速过低,燃料内型面很快会成为直管形。后期可以进一步开展螺旋药形燃速特性方面的研究。螺旋药形的螺纹诱导主流流动从直流变为旋流,可以有效增强火焰层与燃料壁面的热量传递,同时延长燃烧的有效时间,进而大大提高燃料的燃速和燃烧效率。
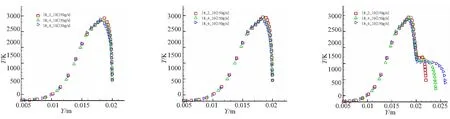
(a) At 333 mm (b) At 336 mm (c) At 339 mm
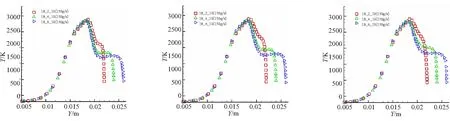
(d) At 342 mm (e) At 344 mm (f) At 346 mm
