基于近场动力学非普通状态理论的高聚物粘结炸药损伤破坏模拟研究

李潘， 郝志明， 刘永平， 甄文强

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

0 引言

近场动力学(PD)方法是一种新的基于非局部思想的无网格方法，主要应用于损伤、破坏、失稳等问题研究[1-2]。最初Silling[3]提出的PD键理论采用对点力描述材料的本构关系，使得泊松比必须为定值，且不能准确地反映材料的黏性、塑性。为了克服上述缺点，Silling等[4]又进一步提出以状态为基础的PD理论，包括普通状态理论和非普通状态理论。其中PD非普通状态理论引入了应力、应变等基本力学参量，能够实现传统本构关系和损伤破坏准则在PD框架下的应用。由于采用节点积分，PD非普通状态理论引起零能模式问题，需要通过添加沙漏力进行控制[5-6]。与有限元、离散元或扩展有限元等方法相比，PD方法将结构离散为带质量的物质点，根据空间积分求解运动方程，消除了网格依赖性和奇异性，损伤自然产生，在求解不连续问题时具有明显优势。

截止目前，学者们基于PD非普通状态理论开展了金属、混凝土、土体等材料的损伤破坏研究。Foster等[7-8]利用PD非普通状态理论模拟了钢板在冲击载荷作用下的裂纹产生和扩展过程。Tupek等[9]将韧性损伤演化模型引入PD，模拟了铝合金在冲击载荷作用下的破坏过程。Fan等[10-12]将PD方法与光滑粒子流体动力学(SPH)方法耦合，模拟了土体在爆炸冲击波作用下的响应。上述工作模拟了结构的损伤演化过程，但没有对损伤过程中应力的分布情况进行分析。文献[13-17]研究了混凝土、岩石等脆性材料中裂纹萌生、扩展以及成核过程，并给出了损伤过程中应力分布。但损伤区域的应力并没有得到应有释放，反而造成应力随损伤演化逐渐增大、与实际不符的情况。

高聚物粘结炸药(PBX)是一种含能材料，广泛应用于国防和国民经济各领域。由于力学行为较复杂，目前PBX损伤破坏研究主要采用有限元、离散元以及扩展有限元等方法[18-19]，PD方法在该方面的研究还比较少见。

本文介绍了PD非普通状态基本理论，求解了运动方程的动态松弛方法，并引入沙漏力控制求解过程中的零能模式。在考虑损伤对PD力状态影响的基础上，提出通过影响函数引入损伤的方法，从而考虑了损伤对近似变形梯度和变形张量的影响。该方法应用于PBX巴西圆盘实验的损伤破坏行为模拟，讨论了沙漏力参数的取值。

1 PD非普通状态理论

1.1 本构关系

PD非普通状态理论的基本方程[4]为

(1)

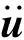
(2)

式中：u为物质点x的位移；u′为物质点x′的位移；η=u′-u为两物质点之间的相对位移。

物质点的近似变形梯度为

(3)

式中：K为形变张量；ω(|ξ|)为作用键的影响函数，它是两点相对位置|ξ|的函数；dVξ为初始构形中物质点x所占的体积。

根据连续介质力学，应变张量可表示为

(4)

式中：I为单位矩阵。

令连续介质力学应变能和PD应变能相等，可得PD力状态的表达式为

(5)

式中：P为第1类Piola-Kirchhoff应力；S为第2类Piola-Kirchhoff应力。

将(5)式代入(1)式，可得非普通状态PD理论的运动方程为

(6)

1.2 运动方程求解

为了将PD方法应用于准静态问题分析，采用自适应动态松弛法对(6)式进行求解，运动方程[20]可以写成：

(7)

在自适应动态松弛法中，为了使运动方程的解尽快收敛到稳定解，每一个载荷步阻尼系数cn都需要重新计算，计算公式为

(8)

由于物质点与其近场范围内其他物质点的弱耦合作用，使得结构出现刚体位移，造成PD非普通状态理论中出现零能模式。控制零能模式需要在力状态的基础上添加沙漏力[5]

(9)

该方法是在物质点x与其近场范围内的所有点之间增加线性弹簧，其弹性常数为cⅠ.

(10)

PD将结构离散为均匀分布的物质点，通过定义两点间的对点力构建点的运动方程，求解运动方程从而得到物质点的速度和位移。本文采用Fortran语言开发了基于PD非普通状态理论的损伤破坏模拟程序。

2 损伤定义

PD方法认为键的伸长率达到临界伸长率时，两点之间的作用键发生断裂。键的伸长率s表达式[21]为

(11)

二维各向同性线弹性材料的键临界伸长率sc表达式为

(12)

式中：K为材料的体积模量；G为剪切模量；Gc为断裂能。

下面基于应力状态定义损伤[13]。首先定义物质点x和x′之间的平均第一主应力

σ1(x,x′)=[σ1(x)+σ1(x′)]/2.

(13)

定义各物质点的局部损伤值

(14)

式中：φ(x,t)取值范围在[0,1]之间，0表示该物质点邻域内无作用键断裂，1表示邻域内的键全部断裂；μ(x,x′,t)为物质点对是否断裂的函数，其表达式为

(15)

ft为材料拉伸强度。

2.1 损伤对力状态的影响

物质点之间的力状态方程(5)式可以改写为

(16)

为了表征研究系统的宏观损伤情况，定义损伤因子d为

(17)

式中：nf为整体离散空间中断裂键总数；ntot为整体离散空间中初始作用键总数。

2.2 损伤对近似变形梯度和变形张量的影响

在结构含初始缺陷或在模拟过程中产生损伤时，采用(16)式只是排除了两物质点之间相互作用力的传递，实际上作用键的断裂还将影响到(3)式中近似变形梯度F和变形张量K的计算。目前PD计算中，文献[13-17]仍考虑已断裂键的作用，造成损伤处应力没有释放。为了克服这一困难，通过影响函数引入损伤

(18)

这样近似变形梯度F和变形张量K中就不再考虑已断裂键的影响，损伤处应力得到相应的释放。对于应变梯度较大的区域，若物质点近场范围内的作用键完全断裂，则形变张量K和近似变形梯度F产生奇异，因此有必要对周围作用键完全断裂的物质点进行特殊处理，即当物质点x与其他物质点不发生作用时，不再对该点的K和F进行计算，直接强制其应变、应力值为0.

3 巴西圆盘实验模拟

3.1 计算模型

PBX9501的巴西圆盘试件如图2(a)所示，圆盘半径R=25.40 mm，厚度W=6.35 mm，将其简化为平面应力问题进行模拟。将巴西圆盘均匀离散为8 273个粒子，相邻粒子间的间距Δx=0.25 mm，近场半径δ=3Δx，离散模型如图2(b)所示。采用方块对巴西圆盘施加位移载荷，2 000个加载步，每步施加位移为1.5×10-4mm. PBX9501的材料参数见表1.

表1 PBX9501材料参数[22]

采用1.2节中添加沙漏力的方法进行零能模式控制，通过零能模式对位移场的影响，确定沙漏力参数取值。图3给出了不同沙漏力参数对x方向位移的影响，从中可以看出：当cI=0时，位移沿x轴的分布曲线产生剧烈振荡；当cI=0.005×1023时，PD方法计算结果偏小，且位移在x轴的端部产生轻微振荡；当cI分别为0.1×1023、0.25×1023、0.5×1023时，PD方法模拟结果与有限元方法结果吻合较好；当cI取值继续增大时，PD方法计算结果越来越偏离有限元方法结果。因此，采用添加沙漏力的方法进行零能模式控制时，参数取值应该控制在一个较精确的取值附近。若取值太小，则零能模式引起的数值不稳定性无法得到有效抑制；若取值太大，则计算结果同样偏离真实值。

图4对cI=0和cI=0.5×1023两种情况下的x轴方向位移云图进行了对比，结果表明不进行零能模式控制时，位移场产生数值振荡，分布云图虚化。选取合适的零能模式控制方法和控制参数，能够使数值振荡得到抑制，从而获得稳定的位移场。

3.2 结果与讨论

3.2.1 仅考虑损伤对力状态的影响模拟结果

采用(16)式引入损伤对力状态的影响，表2给出了巴西圆盘的损伤演化过程。从表2中可以看出，当加载步达到1 212步时，试件在中心开始起裂，形成竖向裂纹，此时中心处表征物质点局部损伤的参数φ约为0.2，即物质点周围的作用键发生部分断裂。随着加载位移的进一步增大，裂纹上下尖端产生应力集中，使得裂纹尖端应力大于材料拉伸强度，裂纹向上下两端快速扩展。在裂纹向两端扩展的同时，已开裂处物质点的损伤进一步加剧，当加载步达到12 16步时，中心处物质点发生断裂。随着越来越多物质点的断裂，宏观裂纹形成。当加载步达到1 230步时，裂纹沿着载荷施加方向形成一条长长的裂纹。从x轴方向位移云图可以看出，损伤的初始阶段，位移基本上是连续的，随着裂纹的扩展以及宏观裂纹的形成，位移表现出明显的不连续性。

表2 巴西圆盘的损伤演化过程

Tab.2 Damage evolution of Brazilian disc

将局部损伤值φ(x,t)≥0.99的物质点删除，从而给出PD方法模拟得到的巴西圆盘试件破坏模式，并与实验结果进行对比。如图5所示，PD数值计算在最后形成一条竖向裂纹，损伤破坏过程与实验基本吻合。但在损伤过程中由于应力得不到有效释放，导致损伤处应力越来越大，影响了损伤过程中的位移和应力分布模拟。造成PD方法模拟结果删除了中间三排物质点，形成较宽的裂纹。

3.2.2 考虑损伤对近似变形梯度和变形张量影响的模拟结果

从表2中的应力云图可以看出，损伤处应力没有得到释放，且数值随损伤演化增大，与实际情况不符。为了解决上述问题，在3.2.1节考虑损伤对PD力状态影响的基础上，再引入损伤对近似变形梯度和变形张量的影响，模拟巴西圆盘的损伤破坏过程。表3给出了改进损伤引入方法之后巴西圆盘的损伤演化过程以及应力分布云图。从表3中可以看出，损伤处应力得到释放，随损伤演化在裂尖处重新集中，从而促使裂纹继续向前扩展，最后形成宏观裂纹，位移呈现明显不连续性。

将局部损伤值φ(x,t)≥0.99的物质点删除得到巴西圆盘的破坏模式，如图6所示。结合图5对比分析发现，除少数位置外巴西圆盘只删除了中间一排点，比之前删除三排点能够更准确地表征真实裂纹开裂情况。但是由于PD方法是一种非局部方法，且非普通状态理论中物质点之间的关联性更强，使得损伤演化过程中有些作用键无法及时断裂，造成损伤跨点传播。

表3 通过影响函数引入损伤后巴西圆盘的损伤演化过程

Tab.3 Damage evolution of Brazilian disc after introducing damage through the influence function

3.2.3 损伤随加载位移的变化

图7将PD模拟结果和实验结果载荷- 位移曲线进行比较，二者吻合较好。PD方法计算得到的试件强度比实验结果稍高，这是由于PD方法采用线弹性损伤模型，没有反映材料的塑性损伤特征。图8给出了载荷和损伤因子随位移的变化，当位移达到0.134 5 mm时，巴西圆盘开始产生裂纹，载荷- 位移曲线呈现非线性特征；随后裂纹迅速扩展，导致载荷剧烈下降；裂纹继续扩展直至贯穿，试件发生完全断裂，与Zhou等[24]测得实验现象一致性很好。

4 结论

本文研究了PD非普通状态理论求解线弹性损伤破坏问题的方法，并应用于PBX巴西圆盘实验的损伤破坏模拟，获得了以下结论：

1) PD非普通状态理论在不进行零能模式控制的情况下，数值振荡明显，得不到合理结果。采用添加沙漏力的方式进行零能模式控制时：若沙漏力参数太小，则零能模式无法得到有效抑制；若沙漏力太大，则结果仍将偏离真实值。因此，需将沙漏力控制在一个合理范围内。

2) 提出通过影响函数的损伤引入方法，从而考虑损伤对近似变形梯度和变形张量的影响，解决了发生损伤处的应力释放问题。模拟了PBX巴西圆盘实验中的裂纹萌生、扩展直至贯穿破坏全过程，试件载荷- 位移曲线、破坏模式与实验结果一致。

参考文献(References)

[1] 黄丹, 章青, 乔丕忠, 等. 近场动力学方法以及应用[J].力学进展, 2010, 40(4): 448-459.

HUANG Dan, ZHANG Qing, QIAO Pi-zhong, et al. A review on peridynamics method and its applications[J]. Advances in Mechanics, 2010, 40(4):448-459. (in Chinese)

[2] Gerstle W, Sau N, Silling S A. Peridynamic modeling of concrete structures[J]. Nuclear Engineering and Design, 2007, 237(12/13):1250-1258.

[3] Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1):175-209.

[4] Silling S A, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2):151-184.

[5] Breitenfeld M S, Geubelle P H, Weckner O, et al. Non-ordinary state-based peridynamic analysis of stationary crack problems[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 272(11):233-250.

[6] Silling S A. Stability of peridynamic correspondence material models and their particle discretizations[J]. Computer Methods in Applied Mechanics and Engineering,2017, 322(15):42-57.

[7] Foster J T, Silling S A, Chen W W. Viscoplasticity using peridynamics[J]. International Journal for Numerical Methods in Engineering, 2010, 81(10):1242-1258.

[8] Foster J T. Dynamic crack initiation toughness: experiments and peridynamic modeling[D]. Lafayette, IN, US: Puedue University, 2009.

[9] Tupek M R, Rimoli J J, Radovitzky R. An approach for incorporating classical continuum damage models in state-based peridynamics[J]. Computer Methods in Applied Mechanics and Engineering,2013, 263(24):20-26.

[10] Fan H, Bergel G L, Li S. A hybrid peridynamics-SPH simulation of soil fragmentation by blast loads of buried explosive[J]. International Journal of Impact Engineering, 2016, 87(1):14-27.

[11] Lai X, Ren B, Fan H F, et al. Peridynamics simulations of geomaterial fragmentation by impulse loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(12):1304-1330.

[12] Ren B, Fan H F, Bergel G L, et al. A peridynamics-SPH coupling approach to simulate soil fragmentation induced by shock waves[J]. Computational Mechanics, 2015, 55(2):287-302.

[13] Zhou X P, Wang Y T, Xu X M. Numerical simulation of initiation, propagation and coalescence of cracks using the non-ordinary state-based peridynamics[J]. International Journal of Fracture, 2016, 201(2):213-234.

[14] Zhou X P, Wang Y T, Qian Q H. Numerical simulation of crack curving and branching in brittle materials under dynamic loads using the extended non-ordinary state-based peridynamics[J]. European Journal of Mechanics A/Solids, 2016, 60(5):277-299.

[15] Zhou X P, Wang Y T. Numerical simulation of crack propagation and coalescence in pre-cracked rock-like Brazilian disks using the non-ordinary state-based peridynamics[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 89(5):235-249.

[16] Wang Y T, Zhou X P, Xu X. Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics[J]. Engineering Fracture Mechanics, 2016, 163(20):248-273.

[17] 谷新保. 近场动力学理论及其在岩石类材料变形过程的数值模拟[D].重庆: 重庆大学, 2015.

GU Xin-bao. Peridynamic theory and its numerical simulation in the deformation and damage process of the rock-like materials[D]. Chongqing: Chongqing University, 2015. (in Chinese)

[18] 黄西成, 李尚昆, 魏强, 等. 基于XFEM与Cohesive模型分析PBX裂纹产生与扩展[J]. 含能材料, 2017, 25(8):694-700.

HUANG Xi-cheng, LI Shang-kun, WEI Qiang, et al.Analysis of crack initiation and growth in PBX energetic material using XFEM-based cohesive method[J]. Chinese Journal of Energetic Materials, 2017, 25(8):694-700. (in Chinese)

[19] 王竟成, 罗景润. 不同细观力学方法预测高聚物粘结炸药有效弹性模量的比较[J]. 兵工学报, 2017, 38(6):1106-1112.

WANG Jing-cheng, LUO Jing-run. Comparison of effective moduli of polymer bonded explosive predicted by different micromechanical methods[J]. Acta Armamentarii, 2017, 38(6):1106-1112. (in Chinese)

[20] Kilic B. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials[D]. Ann Arbor, MI, US: The University of Arizona, 2008.

[21] Kilic B, Agwai A, Madenci E. Peridynamic theory for progressive damage prediction in center-cracked composite laminates[J]. Composite Structures, 2009, 90(2): 141-151.

[22] Tan H, Liu C, Huang Y, et al. The cohesive law for the particle/matrix interfaces in high explosives[J]. Journal of the Mechanics and Physics of Solids, 2005, 53(8):1892-1917.

[23] Liu C, Brownign R. Fracture in PBX 9501 at low rates[C]∥Proceedings of the 12th International Detonation Symposium. San Diego, CA, US: Office of Naval Research, 2002: 11-16.

[24] Zhou Z B, Chen P W, Guo B Q, et al. Quasi-static tensile deformation and fracture behavior of a highly particle-filled compo-site using digital image correlation method[J]. Theoretical and Applied Mechanics Letters, 2011(5):10-13.

[25] Liu C, Thompson D G. Macroscopic crack formation and extension in pristine and artificially aged PBX 9501[R]. Santa Fe, NM, US: Los Alamos National Laboratory, 2010.