地铁隧道钻爆法施工中敏感区间及安全药量确定

2021-02-22贾海鹏刘殿书方真刚田帅康

北京理工大学学报 2021年1期

贾海鹏，刘殿书，方真刚，田帅康

(中国矿业大学力学与建筑工程学院，北京 100083)

为缓解城市交通拥堵，相继有许多城市开始修建地铁. 地铁施工一般都在人口密集区进行，其施工现场有许多学校、居民楼、商业建筑需要保护， “大断面、大埋深、长度大、周边需要保护的建筑多”是地铁钻爆法掘进施工时的特点. 采取措施降低爆破振动对周边建筑结构的影响是城市地铁钻爆法施工的重点和难点. 有许多专家学者在这方面进行了研究，并取得了一定的成果. 孙宝平等[1]采用完全重启动数值模拟技术计算隧道掘进爆破破岩过程，得到了岩体特征点的振动速度. 杨年华[2]根据经验格林函数法原理建立了预测爆破振动的方法，并且编制了专用的预测分析软件；胡建华等[3]利用多元线性回归的方法研究了爆破振动的衰减规律；楼矗云等[4]提出了一种基于样条插值的爆破振动预测方法；夏岸雄等[5]建立了遗传算法优化神经网络的模型来预测爆破振动；蒋莉等[6]基于Levenberg-Marquanh(LM)算法改进BP算法，建立了隧道爆破振动的预测方法；梁书锋等[7]基于回归分析的基本原理，提出了带有安全系数的萨氏优化式. 张小军等[8]将有限个实测样本数据近似为无限样本数据，将正态概率分布应用于爆破振动速度预测，且提出了基于正态分布的振动评价新方法.

爆破振动与地质条件、岩层性质、起爆方式和最大单段药量等因素密切相关. 萨氏公式是使用最广泛的计算爆破振动速度的公式之一. 在萨氏公式中，参数k和α是与地质、地貌有关的参数，其本身就可以反映地质条件和岩层性质对爆破振动的影响.

最大单段安全药量直接影响爆破振动速度的大小，目前，学者对爆破地震波的传播规律研究较多，对爆破设计中的安全控制药量的研究尚不深入. 在隧道开挖掘进过程中，爆源与需要保护建筑物的距离不断变化，不合理的设计药量势必影响工期或者周边建筑结构的安全. 研究新的理论对隧道开挖线路进行分阶段爆破安全药量控制具有十分重要的意义. 文中基于统计学的基本原理，对贵阳地铁2号线爆破施工现场进行振动监测，在大量监测数据的基础上，将t分布应用到隧道开挖线路上的药量控制. 同时，建立了敏感区间计算模型，为优化爆破设计提供了新思路.

1 传统爆破药量计算原理

目前常用的爆破振动速度预测公式主要是萨道夫斯基公式，其形式为

v=K(Q1/3/R)α

(1)

式中：v为爆破振动速度，cm/s；Q为单段最大装药量，kg；R为爆心距，m；K，α为与地质、地貌有关的系数.

将其变成药量形式为

Q=(v/K)3/αR3

(2)

两侧取对数得

(3)

将其变为一元线性形式

Y=bX+lna

(4)

式中：Y=lnQ,X=ln(v/K),b=3/α,a=3lnR.

对实测数据用式(4)进行线性回归，则可以求出未知变量K，α. 进而可以得到萨氏安全药量. 但是，由此方法求出的药量置信度只有50%.

2 基于t分布的爆破安全药量优化计算

2.1 t分布函数的确定

式(1)反映了振速v与比例药量(λ=Q1/3/R)的关系，在具体的爆破施工中，通过确定最大单段药量Q和爆心距R可以预测出场地内某个点位的爆破振动速度v.

大量工程实践发现实测爆破振速在预测爆破振速两侧以某种方式随机分布，可以利用统计学中的理论对其进行研究. 根据统计学原理可知：正态分布适用于无限样本空间且方差未知的事件，t分布适用于有限样本空间且方差未知的事件. 针对具体的爆破施工，现场实测振速数量有限且方差未知,可以用t分布对萨氏公式进行优化.

标准正态分布x～N(0,1)的概率密度函数为

(5)

t分布的概率密度函数可表示为

(6)

式中:t为分布变量；n为样本容量.

伽玛函数可表示为

(7)

式中z为大于0的实数.

t分布适用于小样本事件，可以用小样本均值估计样本总体均值. 如图1所示，相比于标准正态分布，t分布引入了自由度(DF)的概念. DF越大，t概率分布曲线越接近标准正态分布. 所以当t分布中的自由度DF大于一定值时，可以用t分布的有限样本空间去近似正态分布无限样本空间.

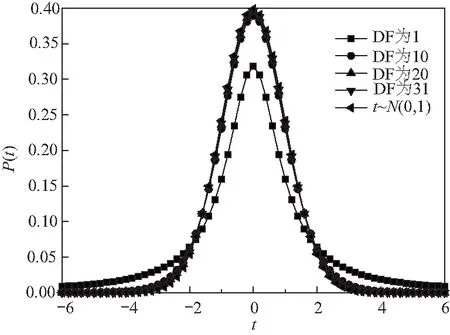
图1 t分布与正态分布对比图Fig.1 Comparison between t distribution and normal distribution

2.2 t分布变化

无限实测振速数据组成事件U，由统计学的规律可知：事件U服从正态分布的特征，可记做：

U～N(μ,σ2)

(8)

式中：μ为振速期望值;σ2为振速方差.

从事件U中抽取数量为n的有限样本组成事件W(对应于现场实测数据)，由中心极限定理可知，随着n的增大，事件W样本均值的分布也服从正态分布，记做：

(9)

对于事件W，其实际标准差σ往往未知，通常用其样本标准差S来代替. 将其做t分布变化

(10)

式中S为样本标准差，其他参数含义同上.

2.3 可靠性概率计算

式(10)服从于自由度DF为n-1的t分布:

(11)

根据式(11)可以确定相应的置信区间(文中置信度取单侧值)，结合其自由度DF，可以计算出置信水平1-φ，则此事件发生的可靠性概率可以表示为

(12)

式中:1-φ为置信水平；P为置信度.

2.4 爆破安全药量计算

假设使目标建(构)筑物得到保护的置信概率为1-φ，通过式(11)可以计算出对应的t值. 结合式(1)，则可得修正振速

(13)

式中：μ为振速期望值，cm/s,可由萨氏公式计算;其他参数含义同上.

由式(2)可得基于t分布的修正安全药量：

(14)

式中：Qt为基于t分布的修正安全药量,kg；vt为基于t分布的修正安全振速, cm/s；K、α为与地形、地貌有关的参数.

基于式(13)可以求出高于99%置信度的基于t分布的修正爆破振动安全振速，则可以由式(14)求出置信度为99%的基于t分布的修正爆破安全药量.

3 爆破振动敏感区间

地铁隧道钻爆施工时，假设与爆源G的距离为R处的一个重要建筑物需要保护. 不改变爆破开挖设计方案时，在爆源向前移动的过程中，周边建筑结构受到的爆破振动是一个“逐渐增大-达到最大值-逐渐减小”的过程,如图2所示.

图2 敏感区间计算原理Fig.2 Principle of calculating sensitive interval

图2中,点F为被保护建筑物，点G为爆源，G、O所在的直线为隧道开挖线路. 被保护建筑物与隧道所在平面交于点C. 在爆源向前推进过程中，点O为隧道开挖线路上距离被保护建筑物距离最近的爆源. 由几何关系可以计算出爆心距为

(15)

式中：R=|FG|为爆心距，m；H=|FC|为被保护建筑物到隧道所在平面的垂直距离，m;D=|OC|为点O爆源与点C的距离，m；L为隧道开挖线路上爆源移动区间(以点O为原点，靠近点O时为负值，远离点O时为正值),m.

在具体的隧道开挖工程中，对于某一个确定的建筑结构，H和D为固定值，由式(15)可知，爆心距R随着L的变化而改变.

以《爆破安全规程》中的安全允许振动速度为计算标准，当爆破振动速度大于安全允许振动速度时，则会存在一个振动速度超标区间，此速度超标区间与相应爆心距Rξ相对应(Rξ为与速度超标区间相对应的爆心距). 由式(15)可知此速度超标区间与某个爆源移动区间相对应，定义此爆源移动区间为敏感区间，记为[-Lξ,Lξ]. 在此区间内，不改变爆破开挖设计方案时，爆破振动速度必然会超出《爆破安全规程》中的安全标准，需要严格控制安全药量，加强对周边建筑结构的保护.

则由式(15)可以得出敏感区间的取值范围为

(16)

式中：Rξ为与速度超标区间相对应的爆心距，m；H为被保护建筑物到开挖平面的垂直距离，m；D为点O爆源与点C的距离。

4 工程应用

4.1 工程概况

贵阳地铁二号线爆破施工现场位于贵阳市观山湖区，其钻爆施工多在人口密集区进行，周边多学校、居民楼和商业建筑需要保护. 测试现场工程概况如图3所示.

图3 工程概况图Fig.3 Project overview diagram

现场监测以爆源为起始点，沿未开挖区方向在隧道正上方采用不同间距布置测点，测点布置采用对数等间距原则，尽可能的减小数据处理带来的误差. 在实际布置测点时，测点前方时常遇路边停车的影响或者部分居民建筑物的遮挡. 应视实际情况对测点位置作出相应调整. 但整体偏差应控制在0～5 m以内. 现场测点布置如图4所示.

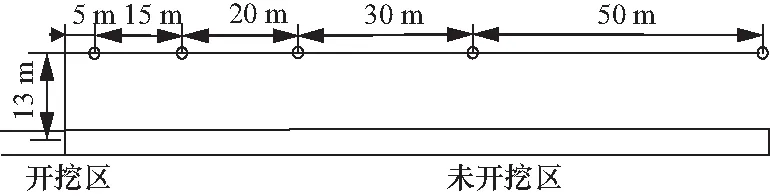
图4 现场测点布置示意图Fig.4 Site measuring point layout diagram

4.2 萨氏安全药量计算

在隧道上方沿隧道开挖方向进行了大量爆破振动速度监测，采集仪触发阈值为0.02 cm/s，除了个别测点未被触发外，其余测点均被触发，共测得32组有效数据，列举部分数据如表1所示.

表1 爆破震动参数记录表Tab.1 Blasting vibration parameter record sheet

注：vI为水平径向的振速；vJ为水平轴向的振速；vZ为垂直向的振速.

对表1数据进行拟合，可以分别得到水平径向、水平轴向和垂直向的萨氏爆破振动速度预测式

(17)

式中：vI、vJ、vZ分别为水平径向、水平轴向和垂直向的爆破振动预测速度,cm/s；Q为单段最大装药量，kg；R为爆心距,m.

将式(17)变换形式，可得萨氏安全药量计算式为

(18)

式中：Qmin为萨氏爆破安全控制药量，kg；v为爆破振动速度, cm/s；R为爆心距,m.

4.3 基于t分布的爆破振动速度计算

基于表1中的爆破振动测试数据，由式(17)可以分别求出水平径向、水平轴向和垂直向的萨氏爆破振动预测速度，结合实测爆破振动速度，可以求出水平径向、水平轴向和垂直向的样本标准差(SI、SJ、SZ)，用(SI、SJ、SZ)替代相应总体标准差(σI、σJ、σZ)，可得水平径向的标准差σI=0.64; 水平轴向的标准差σJ=0.45;垂直向的标准差σZ为0.59.

假设该区域被保护建筑物的置信概率要大于99%. 查t分布表可知置信度为99%且自由度DF为31的置信区间上限单侧值为2.74. 则可以求出自由度DF为31的基于t分布的水平径向、水平轴向和垂直向的修正爆破振动速度预测公式

(19)

式中：vt,I、vt,J、vt,Z分别为水平径向、水平轴向和垂直向的修正爆破振动速度,cm/s；Q为单段最大装药量，kg；R为爆心距,m.

定义λ=Q1/3/R为比例药量，以比例药量为横坐标，三向修正爆破振动速度绝对值为纵坐标，研究其相互关系如图5所示.

图5 修正三向峰值振动速度与比例药量变化关系Fig.5 Correcting the relationship between the three-way peak vibration velocity and the proportional dose

由图5可以看出：当比例药量0<λ≤0.02时，水平径向振动速度最大，垂直向振动速度次之，水平轴向振动速度最小；当比例药量0.02<λ≤0.035时，水平径向振动速度最大，水平轴向振动速度次之，垂直向振动速度最小；当比例药量0.035<λ≤0.043时，水平轴向振动速度最大，水平径向振动速度次之，垂直向振动速度最小；当比例药量0.043<λ≤0.045时，水平轴向振动速度最大，垂直向振动速度次之，水平径向振动速度最小；当比例药量0.045<λ≤0.053时，垂直向振动速度最大，水平轴向振动速度次之，水平径向振动速度最小；当比例药量λ>0.053时，垂直向振动速度最大，水平径向振动速度次之，水平轴向振动速度最小. 从图中可以看出，在隧道掘进过程中采用钻爆法施工时，比例药量决定不同方向爆破震动速度的敏感性.

4.4 基于t分布的安全控制药量计算

由4.3节可知，不同的比例药量会使不同方向的爆破振动速度敏感性有所不同. 定义λ=0.053的比例药量为临界药量. 以λ为判断条件，对隧道钻爆开挖过程中的安全药量控制进行研究.

当比例药量0<λ≤0.053时，安全控制药量接近于0，无法指导爆破施工，此条件无实际工程应用价值，在进行爆破设计时，应该避免此种情况的出现.

当比例药量λ>0.053时，垂直向振动速度最大，此时，只要保证垂直向振动速度达到安全允许标准，则可以保证相应区域内建筑结构的安全. 其安全优化药量计算如下

(20)

式中：Qλ>0.053为基于t分布的安全控制药量，kg；vt,Z为基于t分布的优化爆破振动速度，cm/s；R为爆心距,m.

由式(20)可知：安全控制药量与爆心距正相关，爆心距越小，其安全控制药量也越小.

4.5 工程应用

该施工区域内有一框架结构商业建筑物需要特殊保护，该建筑结构距离爆源所在平面H=13 m，D=15 m，由爆源与被保护建筑结构的位置关系可知，当爆源移动至点O时，其爆心距最小，此时，R=19.8 m.

查阅《爆破安全规程》(GB 6722—2014)，可知工业和商业建筑物的安全许可速度为2.5～5.0 cm/s. 为了最大限度地保护建筑物的安全，这里取下限，即vmin=2.5 cm/s.

由4.4节可知，比例药量λ>0.053具有工程应用价值。其药量应按优化安全药量控制式(20)。

图6 临界药量与优化药量相互关系Fig.6 Relationship between critical and vertical dose

此种情况下，优化药量大于临界药量，应按照优化药量进行爆破设计和施工.

4.6 敏感区间的确定

由图2可以发现，爆源向前移动过程中，爆心距是一个“逐渐减小-达到最小值-逐渐增大”的过程. 由4.5节研究结果可知，以优化药量为标准进行药量控制具有理论依据和现实意义. 本工程中，H=13 m，D=15 m，最大单段药量为Q=10.8 kg，此建筑结构的安全控制振速为2.5 cm/s，则可计算出该建筑结构的敏感区间为[-11,11]. 在此区间内，要优化设计方案，严格控制安全药量，加强对结构的保护.

4.7 敏感区间内外安全药量的确定

当爆源在敏感区间外时(R≥22.69m). 此时，可用式(18)进行药量控制.

当爆源在敏感区间内时，需要加强对建筑结构的保护，此时可用t分布安全药量(式20)进行爆破振动速度控制.

则由式(18)、(20)和(15)可以得到安全控制药量在掘进线路的变化规律，如图7所示.

由图7可以看出:在隧道开挖方向线上,当-∞11 m时，安全控制药量由10.78 kg逐渐增大，且增速越来越大.

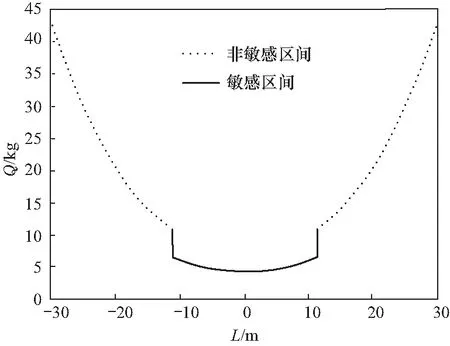
图7 安全控制药量沿掘进线路的变化规律Fig.7 Law of safety control charge along line

所以，在爆源向前移动至敏感区间下限的过程中，安全控制药量逐渐减小. 此阶段需要逐渐减小安全控制药量，适当加快施工进程；在敏感区间范围内，安全控制药量先减小再增大. 此阶段要适当放慢施工进程，严格控制安全药量，最大限度保护建筑结构的安全；在远离敏感区间上限时，安全控制药量急速增加，此阶段可以加大安全控制药量，加快施工进程.