配极理论在圆锥曲线中的应用

刘 悦

（黑龙江省绥化市青冈县永丰镇中学校 黑龙江绥化 151600）

配极理论是以二次曲线性质为基础，逐步形成的理论体系.其系统归纳总结的二次曲线各类性质定理，为中学几何的相关证明，提供了重要理论基础，在解决实际问题上有很好的指导作用，配极理论在二次曲线的学习研究中，系统的阐述了二次曲线一些点和线的关系，以定理的形式归纳得出。

众所周知点共线和线共点问题在中学几何中的常见问题.将配极理论反作用于圆锥曲线，解决中学几何圆锥曲线中的点共线和线共点问题。

一、椭圆中的点共线和线共点A

例1 已知椭圆 的内接三角形△ABC，过，B，C三点分别作椭圆的切线得∆A′B′C′，取任一点S，连结AS，BS，CS，其与对边交点分别是A1，B1，C1.证明 三直线A′A1，B′B1，C′C1交于一点

证 如图1-1所示

∵点S三角形顶点的连线AA1，BB1，CC1交的交点

由题意知u、v、w三点共线

又因为u在A′的极线BC上

∴点A′与点u共轭；

在完全四点形中∵R（b，c；a1u）=-1，

∴A1与u共轭，从而A1A′是u的极线

由共点线的极点必共线，共线点极线必共点可知：A1A′，B′B1，C′C1共点

二、抛物线中的点共线和线共点

例2 证明抛物线的任何方向的平行弦的重点在一直线上，并由此推出这些直线是平行的。

证 设无穷远直线ξ∞与抛物线Γ相切于点O∞，取过点u∞的一组平行弦分别为ab，a′b′...弦的中点分别是m，m′...

由题可知，R（a，b；m，u∞）-1，R（a’，b’:m;，u∞）

∴m，m′在u∞的极线η上，根据配极原则知η必过O∞点

同理，过点V∞的一组平行弦，则V∞的极线T为它的中点轨迹，并有T也过O∞点

∴η∥T

从上述各例可以看出，把配极变换应用于圆锥曲线有关的问题是方便的，当然配极变换的应用并不仅仅限于上述几个方面，有待我们继续探讨。

三、圆的点共线和线共点

例3 过两定点P，Q，分别作圆的两对切线PA，PB，QC，QD，（其中P，Q为圆外两点，A，B，C，D是切点）设AC×BD，AD×CB=R

试证：P，Q，R，G在一条直线上。

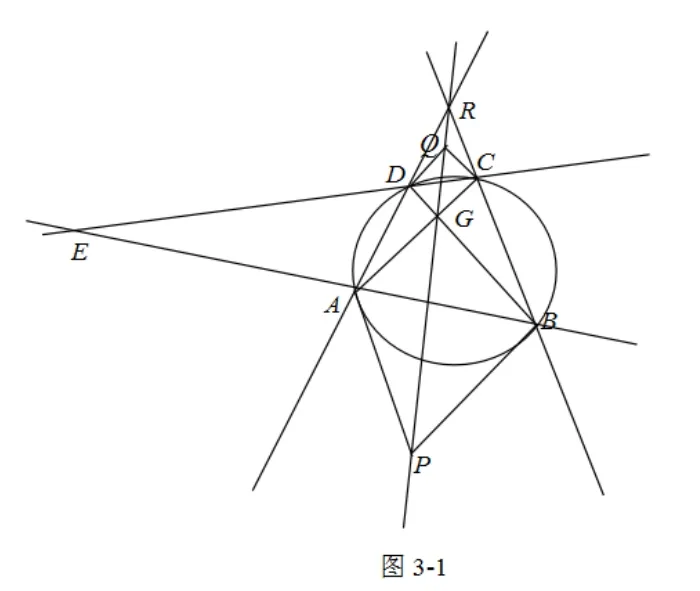
证明 如图3-1，令AB×CD=E，并有点P和点Q的极线分别为直线

AB，CD.

∵AB，CD过点E在，∴根据配极原则可得，点E的极线是PQ

∵ABCD是圆的内接四边形

∴△GER是自配极三点形，E的极线是RG

∵任一点关于同一个圆的极线只有一条

∴直线PQ与RG重合，故P，Q，R，G四点在一条直线上

在配极理论的学习中我们引入了极点与极线等相关的定义，我们将运用高等几何中这些理论，通过实例来讲述在中学几何中常见的平分线段和角平分的问题。利用配极理论中所学知识，通过实际例题来解决中学几何中常见的角平分和平分线段问题。

四、双曲线中的角平分线和平分线段

例4 若双曲线的任一条切线与两条渐近线交于两点，证明切点为这两点所连线段的中点。

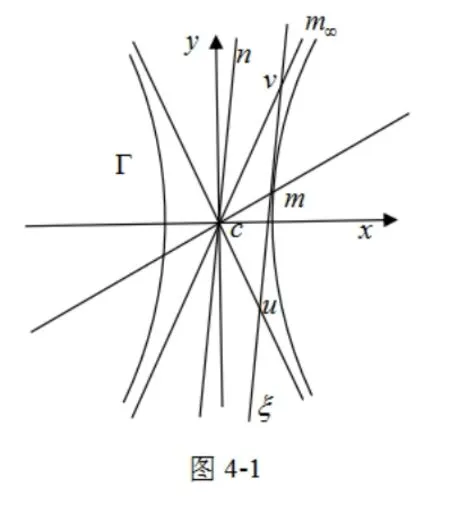
证 令直线ξ为双曲线Γ的任一切线，m为切点.如图4-1所示

ξ与Γ的两条渐近线的两交点为u，v

由已知，ξ的极点是m

∵ξ上的无穷远点m∞，他的极线过直线m和中心c

∴直线cm是m∞的极线

过c作cn∥uv，cn通过m∞，即cn，cn是Γ的一对共轭直径

因为Γ的渐近线调合分离任一对共轭直径

∴R（u，v，m，m∞）-1，也就是（uvm）=-1

因此，线段uv的中点是m

例5 试证明：双曲线的切线被双曲线的渐近线所截线段的中点为切点

证明 如图4-2所示，是按解析几何的观点所作，如图4-3所示，是按射形几何的观点所作。

设两条渐近线分别直线a，b，点p为双曲线的任意一有限点，点p处的切线为l

直线l∞与切线f交于点C∞，a，b与切线f的交点分别为A，B

联结O，P，得OP×l∞=D∞，因l∞为中心O关于曲线 Γ 的极线，且l∞过点D∞，故D∞的极线必过点O，又由点p对应的极线为f，又由于点c∞在f上。

故C∞的极线必过P，而点C∞关于曲线Γ的极线正好是曲线的直径d（可看成一组平行弦RS，A∞B∞，AB...等均过C∞）。

由此可得，关于曲线Γ的自配极三角形是△OC∞D∞，（A∞B∞，C∞D∞）=-1.也就是（ab，dc）=-1.∴（AC，PC∞）-1

即（ABP）=-1，即AP/PB=-1.∴AP=PB

由图4-3，也可得到A’R=SB’

∵AP=PB，曲线Γ的自配极三角形为△OC∞D∞，

∴（AB，PC∞）.所以有能得，（A’B，MC∞）=-1

∴A’M=MB’.又因为D为C∞的极线

∴（RS，MC∞）=-1，RM=MS，故A’R=SB’

五、涉及圆的角平分线和平分线段

例6 过点P，圆的两条切线PA，PB（A，B为切点），且过P作一直线平行于圆上点Q的切线，分别交QA于点E、F，证明 EP=FP（图5-1）。

证明 AB为点P关于圆的极线，设点X为AB与过点Q切线的交点

∵点X在点P的极线AB上

∴点P在X的极线上.又点X在Q的切线上

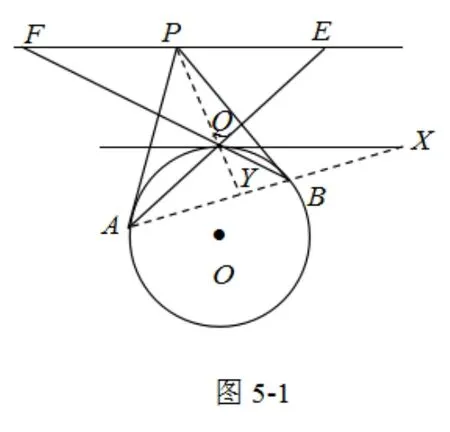
∴Q在X的极线上，因此由极线的定义得（AB，YX）=-1

又∵EF//QX，直线EF截调和线束得（EF，PX∞）=-1

∴点P是线段EF的中点，故EP=FP

例7 从⊙直径AB延长线上一点E引一直线切圆于D，过点A做圆的切线交ED于P，作DC⊥AB垂足为点C，连结PB与DC的交点为M，求证DM=MC（图5-2）。

证明 因为PE为⊙O的切线.D为切点，则PE为D点关于⊙O的极线

又点D在点E关于圆的极线上，DC⊥AB

DC为点E关于圆的极线

所以（AB，CE）=-1.即

而DC//PA，则AC/AE=-BC/BE AC/AE=PD/PE

故由题意DCE和截线PMB得

即，故DM=MC

几何在数学专业中扮演了很重要的角色，高等几何作为其中一门必修课程也体现其重要性，我们现阶段学习高等几何主要是以放射几何为主。主要目的是提高学生的逻辑辩证和空间构造能力。配极理论是其中探索空间最具潜力的一个理论体系。注重理论结合实际是学习高等几何的一大技巧。理论是认识的基础，实践是理论的升华，而应用则是最终目的。