探索中学数学对配极理论的运用

姜广红

（黑龙江省绥化市青冈县哈尔滨师范大学青冈实验中学校 黑龙江绥化 151600）

中学几何中爻于点共线及线共点的、角平分及平分线段、体积、求动点轨迹、数学模型构造作图等问题，能运用高等几何方法去解决。这对于开阔解题的思路，提高解决问题的能力是十分有益的。本文联系中学几何的具体问题，探索配极理论所学的相关知识对一些中学几何命题的运用，并通过实例应用的配极理论探索解决中学几何中体积、求动点轨迹、数学模型构造作图等问题。

一、中学面积及体积问题对配极理论的运用

随着深入学习，渐渐的我们发现，在中学几何的体积问题中，运用配极理论也能便捷的解决一些问题。根据配极中自配极的一些现成定理，我们通过实例来探讨配极理论在中学几何中体积问题的运用。

例1 用配极理论证明，过一点做双曲线的两条切线与渐近线所围成的三角形为等面积三角形

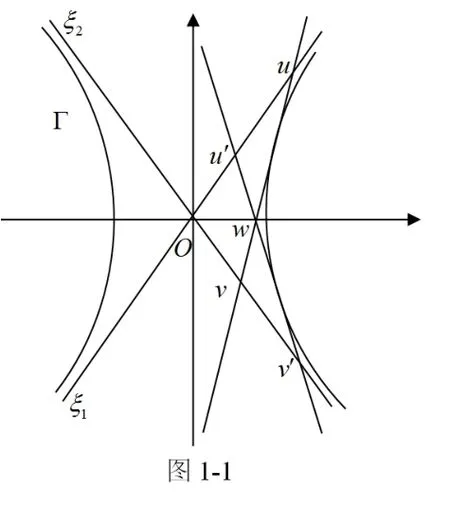
证 如图1-1所示，双曲线Γ的两条渐近线分别为ξ1，ξ2，uv和u′v′是Γ的两条切线，它们与ξ1，ξ2分别组成∆ouv和 ∆ou′v′

∵ξ1，ξ2，uv′，u′v′组成了的完全四线形，又三条对顶线uv′，u′v，ow组成一个自极三线形

因为ow是Γ的直径，uv′与u′v′的交点是它的极点，这个交点又在无穷远直线上

∴uv′//u′v′，S∆n′v′v=S∆nvu′，S∆n′v′v+S∆ou′v=S∆uvu′+S∆ou′v

故S∆ouv=S∆ou′v′

二、点轨迹问题对配极理论的运用

谈到轨迹问题，我们一定不会陌生.怎样快速的找到一个动点的轨迹规律，找出轨迹方程是我们中学学习的重中之重。这一章我们将利用高等几何中学习的配极理论来探讨一下关于中学轨迹的别样求法。

例2 若A，B两点为椭圆上的每条切线与圆x2+y2=25交点，m为过A，B关于已知圆的切线的交点，求m的轨迹方程。

解 若为椭圆上任一点，由题意可知过m0的椭圆切线方程为

它的射影坐标方程是

根据题意，m0的射影方程即为点m关于圆的极线

设m的射影坐标为(x1′,x2′,x3′)，则有

解得

由此可知m0的射影坐标是

∴m0的坐标是

所以得将其代入方程得

即m0的轨迹为一个椭圆。

例3 作抛物线y2=6x的切线，过点（8，13），求其切线的轨迹方程。

解 由题

即为切点

故所求方程为3x−2y+2=0或x−8y+96=0

其中Sp=0即为点P(8,13）关于抛物线的极线方程。

三、中学作图问题对配极理论的运用

学习数学，数学模型的快速构造是我们基本技能之一，学习好这一基本技能对于我们快速的解决一个实际问题将有不可替代的作用。

我们将以配极理论所学，通过实例阐述配极理论对于作图的应用

例4 以直尺作圆外定点的切线解析

作法 如图3-1.设O及圆外一点P，过P点任做二割线分别交圆于A,B和C,D四点；

连结AC与BD交于点M，连结AD与BC交于点N，连结MN与圆交于X,Y两点；连结PX，PY，得PX和PY即为所求切线。

证明 因四边形CABD为圆的内接四边形，则定义得，PMN为自极三角形。从而P点关于圆的极线为MN。又因MN通过圆上两点X,Y，由题意知X,Y关于圆的极线都通过P点。又根据性质，PX，PY分别为X，Y关于圆的极线，亦为圆在X，Y处的切线。

例5 以直R作出过椭圆外一点关于椭圆的切线

解 我们知道解决此类问题的关键点是找到切点。根据配极原则可知，交点为圆锥曲线外一点关于曲线切线的切点是此点的极线与圆锥曲线的交点，所以根据自配极三点形的概念，作图如下：

设点P是椭圆外的任一点，经过点P任作PAB和PCD两条割线交椭圆于点A，B和C，D，并令AC×BD=Q，AD×BC=E，连接QE，与椭圆于点M，N，可得M，N为两切点

证明 因为椭圆的内接四边形为四边形ABCD，∆PQE是自极三点形，也即QE为P的极线

也就是说QE与椭圆的两个交点M，N即为切点

即PM，PN为所求两条切线

四、中学其他问题对配极理论的运用

我们知道，科学是不断往前发展的，对于配极理论在中学几何中的应用远远不止这些，需要我们不断的去努力发现这个规律的更多应用，为人类发展作出更大贡献。通过收集整理，得到以下一些关于配极理论应用新的方向。

例6 试用配极理论证明三角形的垂心是三角形的三条高的交点

证 作∆ABC，以∆ABC的外接圆做∆ABC的配极三角形TUV，

如图4-1所示，因为A的极线为UV，所以AP的极点A2与BC的极点T对于点O所成的角是直角.也即∠A2OT=900

于是有A2是过O所作出的OT的垂线与UV的交点，同样可以作出B2，C2来

由配极原则知，A2，B2，C2应在同一直线上

综上所述：三角形的垂心是三角形的三条高交点。

例7 试用根据配极理论证明三角形两边中点连线与第三边平行

证明 如图4-2.设M，N分别是 ∆ABC的边BC，AC的中点，过A，B，C作∆ABC的外接圆O的外切∆TUV

则由题可知ABC与∆TUV互为配极三角形，TV，TU为B，C的极线

由于M在S1=0之上，故T在M的极线上，且M的极线与OM垂直

故∠U的外角平分线为M的极线

又由于，平行直线AB和MN的极线与其垂直

也就是为∠V的平分线，MN的极点是∆TUV的一内角平分线与两外角平分线的交点S

综上所述：三角形两边中点连线与第三边平行

在学习中，不难发现高等几何是初等几何的延伸，其拓展了中学几何的思维空间，让我们了解到高等几何在几何学中学习的不可取代性，对中学几何知识和许多问题有了更深入的领会，能从更多的角度思考、更快更便捷的解决问题。学习好高等几何不但能增强处理初等几何问题的能力，而且在平时的工作生活中也是培养逻辑思维的一种有效途径。