有向图的无符号拉普拉斯谱半径的新上下界

何 军， 刘衍民， 冉 杰

(遵义师范学院 数学学院， 贵州 遵义 563006)

1 预备知识

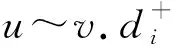
Q(G)=A(G)+D(G).

因为有向图G是一个连通图，则有向图G的无符号拉普拉斯矩阵Q(G)为一个非负不可约的矩阵[1].设无符号拉普拉斯矩阵Q(G)的特征值由大到小排列为

q1(G)≥q2(G)≥…≥qn(G)，

则称q1(G)为有向图G的无符号拉普拉斯谱半径.

对于无向图G的无符号拉普拉斯谱半径的研究已经取得了很多不错的成果.最早，Cvetkovic等[1]给出了图G的无符号拉普拉斯矩阵的定义,文献[2-3]给出了图G的无符号拉普拉斯谱半径与拉普拉斯谱半径之间的大小关系,但目前对有向图G的无符号拉普拉斯谱半径的研究工作还相对较少.

2016年，Xi等[4]利用有向图顶点的度数，给出了有向图G的无符号拉普拉斯谱半径q1(G)的上界

(1)

2 主要结果

引理1[5]设M是一个非负不可约矩阵，则它的谱半径ρ(M)是M的一个特征值，且存在一个正向量X，使得MX=ρ(M)X.

引理2[6]设M是一个n阶非负方阵，Ri(M)是它的第i行的行和,则

min{Ri(M):vi∈E(G)}≤ρ(M)≤
max{Ri(M):vi∈E(G)}，

等式成立当且仅当行和相等.

定理1设G是一个n阶连通有向图,则

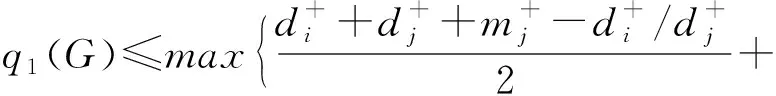
(2)

证明令有向图G的出度对角矩阵

X=(x1,x2,…,xn)T

是矩阵D(G)-1Q(G)D(G)的最大特征值q1(G)所对应的特征向量.设

xi=max{xk:1≤k≤n}=1，
xj=max{xk:k≠i},

因为

D(G)-1Q(G)D(G)X=q1(G)X，

(3)

考虑(3)式中的第i个等式,有

又因为xi=1是特征向量里面的最大值，且

xj=max{xk:k≠i},

有

(4)

再考虑(3)式中的第j个等式,有

即

(5)

由(4)和(5)式可得

即

证毕.

定理2设G是一个n阶连通有向图,则

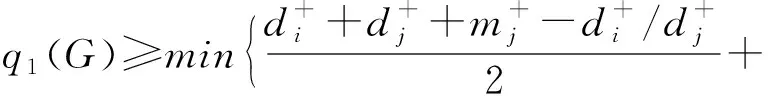
(6)

证明令有向图G的出度对角矩阵

X=(x1,x2,…,xn)T

是矩阵D(G)-1Q(G)D(G)的最大特征值q1(G)所对应的特征向量.设

xi=min{xk:1≤k≤n}=1，
xj=min{xk:k≠i}，

因为

D(G)-1Q(G)D(G)X=q1(G)X，

(7)

考虑(7)式中的第i个等式,有

又因为xi=1是特征向量里面的最小值，且

xj=min{xk:k≠i},

有

(8)

再考虑(7)式中的第j个等式,有

即

(9)

由(8)和(9)式可得

即

证毕.

如果令定理1和定理2中的对角阵为

R=diag(1,1,…,1)，

那么可得定理3.

定理3设G是一个n阶连通有向图,则

3 数值例子

下面用数值例子来说明结果的有效性.设有向图G的邻接矩阵

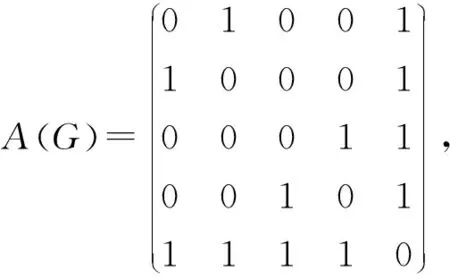
那么有向图G的无符号拉普拉斯矩阵谱半径q1(G)=5.561 6.由(1)式可得q1(G)≤7.372 3，由(2)式可得q1(G)≤6.000 0,即定理1的结果优于文献[4]中定理12的结果.

致谢遵义师范学院博士基金资助项目(遵师BS[2015]09)对本文给予了资助，谨表谢意.

[1] CVETKOVIC D, DOOB M, SACHS H. Spectra of Graphs[M]. New York:Academic Press,1980.

[2] SHU J L, HONG Y, WEN R K. A sharp upper bound on the largest eigenvalue of the Laplacian matrix of a graph[J]. Linear Algebra Appl,2002,347(1/2/3):123-129.

[3] YAN C. Properties of spectra of graphs and line graphs[J]. Appl Math J Chin Uni,2002,17(3):371-376.

[4] XI W G, WANG L G. Sharp upper bounds on the signless Laplacian spectral radius of strongly connected digraphs[J]. Discussiones Mathematicae Graph Theory,2016,36(4):977-988.

[5] HORN A, JOHNSON C R. Matrix Analysis[M]. New York:Cambridge University Press,2013.

[6] BOZKURT S B, BOZKURT D. On the signless Laplacian spectral radius of digraphs[J]. Ars Combinatoria,2013,108(108):193-200.