拟从属关系定义的双单叶解析函数类

马 烁, 王安平

( 1. 荆州理工职业学院 基础课部, 湖北 荆州 434032; 2. 武汉商学院 信息工程学院, 湖北 武汉 430056; 3. 长江大学 工程技术学院, 湖北 荆州 434020)

用A表示单位圆盘U={z∈C:|z|<1}内解析且具有如下展开式的函数族

(1)

其中

(2)

函数f(z)∈S称为U内的双单叶函数当且仅当f(z)和f-1(z)均为U的单叶函数,现记Σ表示U中具有(1)式的双单叶函数族.α阶星形函数类S*(α)和α阶凸函数类K(α)定义为

0≤α<1},

z∈U,0≤α<1}.

从上述表达式可以看出

f(z)∈K(α)⟺zf′(z)∈S*(α).

设f(z)和φ(z)在U内解析,称f(z)从属于φ(z),记作f(z)φ(z),若存在U内的Schwarz函数ω满足ω(0)=0,|ω(z)|<1,使得

f(z)=φ(ω(z)).

进一步,称f(z)拟从属于[1]φ(z),记为

f(z)qφ(z).

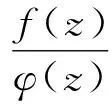
f(z)qφ(z)⟺f(z)=φ(z)φ(ω(z)),

其中ω(z)为Schwarz函数且|φ(z)|≤1.特别地,当φ(z)≡1时,从属与拟从属的定义完全一致.上述φ(z)在U内解析且具有正实部.为了叙述方便,本文假设

φ(z)=A0+A1z+A2z2+…, |φ(z)|≤1, (3)

φ(z)=1+B1z+B2z2+…,B1>0.

(4)

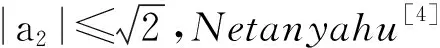
设f(z)由(1)式给出,k(z)由下式给出

f(z)与k(z)的卷积f*k定义为

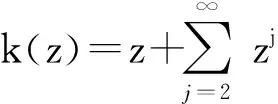
定义1若f(z)∈Σ由(1)式给出,且满足拟从属关系：

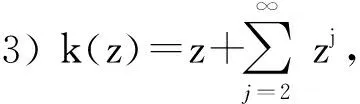
定义2若f(z)∈Σ由(1)式给出,且满足拟从属关系：

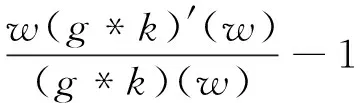
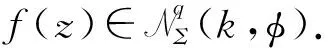
定义3若f(z)∈Σ由(1)式给出,且满足拟从属关系：

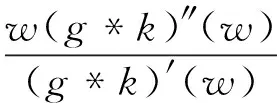
其中,g=f-1由(2)式定义,φ由(3)式定义,φ由(4)式定义,则称

1 主要结论

为了得到本文的结论,需要用到下面引理.

引理1[21]若h∈A,且满足h(0)=1,在U内具有正实部,则|ck|≤2,k=1,2,…,这里

h(z)=1+c1z+c2z2+…,z∈U.

引理2[22]若h∈A,且满足h(0)=1,在U内具有正实部,且

h(z)=1+c1z+c2z2+…,z∈U,

则

φ(z)[φ(u(z))-1],

(5)

φ(w)[φ(v(w))-1],

(6)

其中g=f-1.现在定义函数p(z)、q(w)如下:

这等价于

容易看出,p(z)、q(w)在U内解析,且满足p(0)=q(0)=1,在U内具有正实部.因此由引理1,得|ci|≤2,|di|≤2.由(3)、(4)、(7)、(8)式得

(9)

(10)

将f、g、k的解析式代入得

(1+λ)a2b2z+(1+2λ)a3b3z2+…,

(11)

-(1+λ)a2b2w+

(12)

由(7)～(12)式,并比较两边的系数得:

(13)

(14)

(15)

(16)

由(13)和(15)式得:

c1=-d1,

(17)

(18)

(14)和(16)式两边相加,并利用(17)式得

(19)

利用|ci|≤2,|di|≤2,i=1,2,并结合(13)与(19)式得

下面得出|a3|的估计.用(14)式减去(16)式得

利用(18)式并结合|ci|≤2,|di|≤2,i=1,2,得

(20)

利用(19)式并结合|ci|≤2,|di|≤2,i=1,2,得

结合(21)式和(22)式即可得

推论2若由(1)式定义的函数f(z)∈BΣ(n,λ,φ),那么

注意到以下事实,经过简单的推导可知

对比文献[8]的结论,可以发现本文的推论2比文献[8]的估计结论更为精确,同时也比文献[9,11]精确.

|a2|≤min{J,K,L},

|a3|≤min{M,N,P},

其中

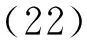
其中,g=f-1,定义的函数p(z)、q(w)同定理1.对(22)和(23)式左边进行展开,并将f、g、k的解析式代入得

结合(9)、(10)式,并比较(22)、(23)式两边的系数得:

(24)

(25)

(26)

(27)

由(24)和(26)式得:

c1=-d1,

(28)

(29)

4a2b2=A0B1(c1-d1).

(30)

(25)和(27)式两边相加,并利用(28)和(30)式得

(31)

(25)和(27)式两边相加,并利用(24)和(28)式得

(32)

(25)和(27)式两边相加,并利用(24)和(29)式得

(33)

利用(31)～(33)式,结合引理1,即可得到|a2|的估计值.

下面得出|a3|的估计.用(25)式减去(27)式得

(34)

将(32)式代入(34)式得

(35)

利用(25)式减去(27)式,并利用(31)式得

(36)

或者将(36)式整理得

4b3a3=

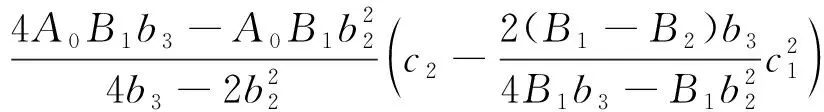
(37)

结合(35)～(37)式和引理2即可得到定理的结论.因此定理得证.

在定理2中,令b2=1,b3=1,很容易得到推论3.

|a2|≤min{J1,K1,L1},

|a3|≤min{M1,N1,P1},

其中

注意到,推论3中系数|a2|的系数中有一项为|a2|≤L1,这刚好是文献[23]的结论,因此推论3中的结论比文献[23]更精确的估计了|a2|的上界.

推论4若由(1)式定义的函数f(z)∈S*(Σ,φ),则:

|a2|≤min{J2,K2,L2},

|a3|≤min{M2,N2,P2},

其中

N2=B1+|B2-B1|,

|a3|≤

u(0)=v(0)=0,

|u(z)|<1, |v(w)|<1,

且使得:

(38)

(39)

其中g=f-1,定义的函数p(z)、q(w)同定理1.对(38)和(39)式左边进行展开,并将f、g、k的解析式代入得

结合(9)、(10)式,并比较(38)、(39)式两边的系数得:

(40)

(41)

(42)

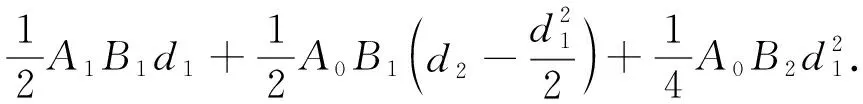
由(40)和(42)式得:

c1=-d1,

(44)

(45)

8a2b2=A0B1(c1-d1).

(46)

(41)和(43)式两边相加,并利用(46)式得

(47)

利用(46)、(47)式,结合引理1,即可得到|a2|的估计值.

下面得出|a3|的估计.用(41)式减去(43)式,并利用(44)式得

(48)

将(47)式代入(48)式得

4A0B1c2+2A1B1(c1-d1).

(49)

将(45)或(46)式代入(48)式得

(50)

结合(49)、(50)式和引理1即可得到定理的结论.因此定理得证.

推论5若由(1)式定义的函数f(z)∈Kq(Σ,φ),则

|a3|≤

注意到,推论5中系数|a3|中有一项估计为

这刚好是文献[23]的结论,因此推论5的结论比文献[23]更精确了.

在推论5中,令φ(z)=1,即令A0=1,A1=0,得下面推论.

推论6若由(1)式定义的函数f(z)∈K(Σ,φ),则

[1] ROBERTSON M S. Quasi-subordination and coefficient conjectures[J]. Bull Am Math Soc,1970,76(1):1-9.

[2] LEWIN M. On a coefficient problem for bi-univalent functions[J]. Proc Am Math Soc,1967,18(1):63-68.

[3] BRANNAN D A, CLUNIE J G. Aspects of Contemporary Complex Analysis[M]. New York:Academic Press,1979.

[4] NETANYAHU E. The minimal distance of the image boundary from the origin and the second coefficient of a univalent function in |z|<1[J]. Arch Rational Mech Anal,1969,32(2):100-112.

[5] LASHIN A Y. On certain subclasses of analytic and bi-univalent functions[J]. J Egyptian Mathematical Society,2016,24(2):220-225.

[6] XU Q H, GUI Y C, SRIVASTAVA H M. Coefficient estimates for a certain subclass of analytic and bi-univalent functions[J]. Appl Math Lett,2012,25(6):990-994.

[7] SRIVASTAVA H M, MISHRA A K, GOCHHAYAT P. Certain subclasses of analytic and bi-univalent functions[J]. Appl Math Lett,2010,23(10):1188-1192.

[8] 李小飞,秦川. 一类利用从属关系定义的双单叶函数类[J]. 四川师范大学学报(自然科学版),2014,37(4):511-514.

[9] 熊良鹏,李小飞,刘晓丽. 受限于从属族的bi-单叶函数的系数边界[J]. 河南师范大学学报(自然科学版),2013,41(3):15-18.

[10] JANOWSKI W. Some extremal problems for certain families of analytic functions[J]. Int Ann Polon Math,1973,28(3):298-326.

[11] FRASIN B A, AOUF M K. New subclasses of bi-univalent functions[J]. Appl Math Lett,2011,24(9):1569-1573.

[12] DENIZ E. Certain subclasses of bi-univalent functions satisfying subordinate conditions[J]. J Classical Analysis,2013,2(1):49-60.

[13] JUMA A S R, AZIZ F S. Applying Ruscheweyh derivative on two subclasses of bi-univalent functuions[J]. Int J Basic Appl Sci,2012,12(6):68-74.

[14] BRANNAN D A, TAHA T S. On some classes of bi-univalent functions[J]. Math Anal Appl,1986,31(2):53-60.

[15] ALGAHTANI O. Estimates of initial coefficients for certain subclasses of bi-univalent functions involving quasi-subordination[J]. J Nonlinear Sci Appl,2017,10(3):1004-1011.

[16] GOYAL S P, KUMAR R. Coefficient estimates and quasi-subordination properties associated with certain subclasses of analytic and bi-univalent functions[J]. Math Slovaca,2015,65(3):533-544.

[17] KUMAR S S, KUMAR V, RAVICHANDRAN V. Estimates for the initial coefficients of bi-univalent functions[J]. Tamsui Oxford J Information & Mathematical Sciences,2012,29(4):487-504.

[18] GOYAL S P, SINGH O, MUKHERJEE R. Certain results on a subclass of analytic and bi-univalent functions associated with coefficient estimates and quasi-subordination[J]. Palestine J Math,2016,5(1):79-85.

[19] GOYAL S P, SINGH O. Estimates of quasi-subordination classes[J]. J Rajasthan Academy Phys Sci,2014,13(2):133-142.

[20] MAGESH N, BALAJI V K, YAMINI J. Certain subclasses of bi-starlike and bi-convex functions based on quasi-subordination[J]. Abstract and Applied Analysis,2016,2016(2):1-6.

[21] POMMERENKE C H. Univalent Functions[M]. Berlin:Springer-Verlag,1975.

[22] KEOGH F R, MERKES E P. A coefficient inequality for certain classes of analytic functions[J]. Proc Am Math Soc,1969,20(1):8-12.

[23] KANT S, VYAS P P. Certain subclasses of bi-univalent functions associate with quasi-subordination[J]. Rajasthan Academy of Physical Sciences,2016,15(4):315-325.