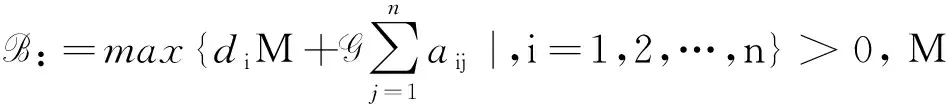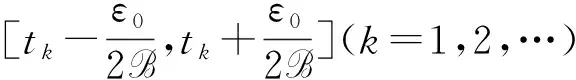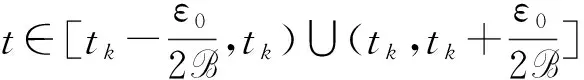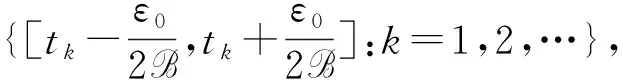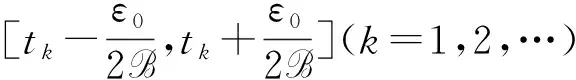时滞Hopfield神经网络全局渐近稳定的弱条件
2018-06-04宿娟
宿 娟
(成都师范学院 数学学院, 四川 成都 610044)
Hopfield神经网络由美国加州物理学家Hopfield[1]于1984年提出,由于在优化问题[2-5]、模式识别[6]和协同记忆[7]等方面的广泛应用,该网络自提出以来就受到科学家们的持续关注.关于该网络及其各种推广的研究不断涌现[8-11].然而在网络的实际应用中,时滞的出现不可避免.对含时滞的Hopfield神经网络的动力学行为的研究也在文献[12]之后不断出现,取得了突破性的进展[13-18],其中文献[13]研究如下时滞Hopfield神经网络
i=1,2,…,n,
(1)
xi(t)表示第i个神经元在t时刻的状态变量,di>0表示网络在不连通且无外部附加电压差的情况下第i个神经元恢复孤立静息状态的速率,aij∈R表示第j个神经元对第i个神经元的影响强度,gj∈C(R)表示神经元的输出函数,也称为激活函数,时滞τij>0,Ii∈R表示外部输入.系统(1)满足初值条件
xi(t)=φi(t),t∈[-τ,0],
(2)
其中,τ:=max{τij:i,j=1,2,…,n},φi∈C([-τ,0],R).针对经典的激活函数gj(s)=tanh(μjs),其中μj(j=1,2,…,n)为非零常数,文献[13]得出若满足
(3)
则系统(1)存在唯一平衡点并且是全局渐近稳定的.进一步文献[14]削弱文献[13]中对激活函数gj具体形式的限制,仅假定其满足有界和Lipschitz条件,得到系统(1)存在唯一的平衡点并且是全局渐近稳定的充分条件:
(4)
其中Lj>0是激活函数gj的Lipschitz常数.显然tanh(μjs)满足文献[14]中激活函数的要求,并且Lipschitz常数为|μj|.同时比较(3)和(4)式,容易得出文献[14]推广了文献[13]的工作.文献[15]则再次削弱了对gj的要求,假设只满足Lipschtz条件,得到系统(1)存在唯一平衡点并且全局渐近稳定的一个充分条件:DL-1-|A|为M-矩阵,其中D:=diag{d1,d2,…,dn},L:=diag{L1,L2,…,Ln}和|A|:=(|aij|)n×n.为了明确条件(4)式和DL-1-|A|为M-矩阵的关系,回顾文献[15]中引理1关于M-矩阵的等价定义.得到结论如下:DL-1-|A|为M-矩阵当且仅当存在向量γ=(γ1,γ2,…,γn)>0,使得γ(DL-1-|A|)>0,这里“>0”表示向量的每个分量均大于0.特别当γi=1,i=1,2,…,n时
γ(DL-1-|A|)=
显然γ(DL-1-|A|)>0当且仅当不等式(4)成立.由此说明(4)式是DL-1-|A|为M-矩阵的一个充分条件,从而文献[15]推广了文献[14]的结论.
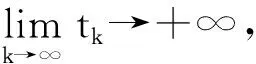
回顾上述全局渐近稳定条件[13-15],其中均要求严格不等.究其原因,在于Lyapunov函数的应用.准确的说,为了得到平衡点的全局渐近稳定,需要对所构造的Lyapunov函数沿系统(1)的解的导数严格小于零,以此保证平衡点的全局渐近稳定性.因此,条件(3)和(4)式以及M-矩阵等价条件中的严格不等就是为了Lyapunov函数沿系统解的导数严格小于0.至此一个很自然的问题产生:能否将条件的“<0”弱化为“≤0”?事实上对这样的弱化问题,当系统(1)不含时滞,即τij=0时,文献[19-20]分别针对不同激活函数进行了研究.文献[19]研究系统(1)中τ=0,gj(s)=tanh(μs),其中μ>0时全局吸引的弱条件,这里弱条件体现在将文献[21]工作中全局吸引的条件中的“<0”弱化至“≤0”.文献[20]则研究了系统(1)中τ=0,矩阵A:=(aij)n×n对称,gj满足0 受文献[14-15,19-20]的启发,本文研究时滞系统(1)全局渐近稳定的弱条件.首先仍然需要构造Lyapunov函数,并计算该函数沿系统(1)解的导数,通过导数非正证明了系统(1)平衡点的稳定性.然后综合利用反证法等基本分析方法证明该平衡点是全局吸引的.这里得到的吸引性条件体现了将已有结论中的严格小于弱化为不大于.由此给出系统(1)全局渐近稳定的一个弱条件. 本文假设激活函数gj(j=1,2,…,n)满足Lipschitz条件,即存在常数Lj>0满足 (H1) |gj(s1)-gj(s2)|≤Lj|s1-s2|,∀s1,s2∈R. Lipschitz条件(H1)并不能确保系统(1)的平衡点的存在性.以下列一维系统为例 (5) i=1,2,…,n, (6) 其中 y(t):=x(t)-x*, j=1,2,…,n. (7) 并且由(H1)还得到 ∀s∈R,j=1,2,…,n. (8) 除了假设(H1),还假设gj满足 证明定义 j=1,2,…,n. (10) 显然 根据(H1),容易得到 |D+gj(s)|≤Lj,j=1,2,…,n. (12) 从(9)式计算D+Fj,并根据(12)式得到 D+Fj(s)=-D+gj(s)+Lj≥0, ∀s∈R,j=1,2,…,n, (13) 其中D+表示右下Dini导数.根据文献[22]附录I中的定理2.1,从不等式(13)得出Fj在R上单调不减.进一步由(H2)和(9),计算得到 j=1,2,…,n, (14) (15) 将(9)式中Fj的定义代入(15)式,得到 j=1,2,…,n. (16) 同理,对Hj(j=1,2,…,n)也成立 (17) 将(10)中Hj的定义代入(17)式,得到 j=1,2,…,n. (18) 综合(16)和(18)式,下列不等式成立 引理得证. 在上述准备工作的基础上,下面将给出系统(1)全局渐近稳定的条件和具体证明. 定理2.1设系统(1)存在平衡点,gj(j=1,2,…,n)满足(H1)和(H2).若存在常数γi>0使得 则系统(1)的平衡点唯一并且是全局渐近稳定的. 证明证明分成3步完成. 第一步,构造Lyapunov函数,证明系统(6)的零解的稳定性.定义 (19) 计算V(t)沿系统(6)的解的右上Dini导数,得到 利用(8)式进一步化简(20)式,得到 根据α≤0,从(21)式得出 D+V(t)≤0, (22) 说明系统(6)的零解是稳定的. 第二步,假设系统(6)的零解不吸引,从而对某个j∈{1,2,…,n},估计|yj(t)|在t属于某个区间列时的上界和正的下界. 首先估计|yj(t)|,j=1,2,…,n的上界.显然(22)式说明函数V(t)单调递减,同时由于V(t)≥0,得出 (23) 结合V(t)的定义(19)式以及(23)式,将采用反证法得出如下结论:存在某个时间t′以及常数M>0,满足 |yj(t)|≤M, ∀t>t′,j=1,2,…,n. (24) (25) 将(25)式结论用于V(t)的定义式(19)中,得到 V(ξk)≥γj0|yj0(ξk)|→+∞,k→+∞, t>t0,i,j=1,2,…,n}<+∞. (26) 将(24)和(26)式应用于(6)式,得到下列估计式 ∀t>t0,i=1,2,…,n, (27) 再次根据假设系统(6)的平凡解不吸引,必然存在y(t)的某个分量,不妨记为yj*(t)满足 yj*(t)→/0,t→∞. (28) |yj*(tk)|≥ε0. (29) 此外还假定序列{tk}满足 利用(29)式可得下面的估计 k=1,2,…. (31) (32) 其中ξ∈(tk,t)或(t,tk),从而(31)式仍然成立. 综合(24)和(31)式,存在某个j*∈{1,2,…,n}满足 第三步,利用(33)式,将证明当t属于某个区间列时,D+V(t)存在一个上界为负,由此与V(t)≥0矛盾.再从(20)式得到 (34) 下面分2种情况从(34)式推导与V(t)非负的矛盾: (C1) 存在某个i0∈{1,2,…,n}满足ai0j*≠0; (C2) 对所有的i∈{1,2,…,n},满足aij*=0, 其中下标j*由(28)式给出.在对(C1)进行讨论之前,首先利用α≤0对(34)式化简得到 Lj|yj(t-τij)|}≤ Lj|yj(t-τij)|}. (35) Lj*|yj*(t-τj*)|}. (36) 于是在(C1)情况下对(36)式右端放大得到 D+V(t)≤-γi0|ai0j*|{Lj*|yj*(t-τi0j*)|- (37) D+V(t)≤-γi0|ai0j*||yj*(t-τi0j*)| (38) 结合引理1.1和紧性,容易得出 (39) D+V(t)≤-Ω, (40) D+V(t)≤0. (41) k→∞, (42) (43) 于是在(C2)条件下,利用定理2.1条件中α≤0,从(43)式得出 -γj*dj*|yj*(t)|. (44) 于是将(33)式应用到(44)式中,进一步得到 D+V(t)≤-ε0γj*dj*/2<0, D+V(t)≤0. (46) k→∞, (47) 这和V(t)非负矛盾.综合(C1)和(C2)的结论,都得出矛盾,由此说明第二步中的假设(28)式不成立,从而系统(6)的零解吸引.考虑到第一步的结论:系统(6)的零解是稳定的,得到该系统零解是全局渐近稳定的.于是原系统(1)的平衡点是全局渐近稳定的,因此平衡点唯一.定理得证. 注1定理2.1中条件(H1)和α≤0并不能保证系统平衡点的存在.例如一维系统(5)满足(H1),并且对任意γ>0都有α=0.但是当I>0是并不存在平衡点.因此该定理中假设系统(1)存在平衡点是必要的. 注2利用文献[15]中引理1得到下列事实:DL-1-|A|∈M-矩阵,当且仅当存在γj>0,j=1,…,n,满足 即α<0.显然定理2.1中全局渐近稳定的条件α≤0较文献[15]给出的DL-1-|A|∈M-矩阵这一个条件弱. [1] HOPFIELD J. Neurons with graded response have collective computational properties like those of two-stage neurons[J]. Proc Natl Acad Sci USA,1984,81:3088-3092. [2] TANK D, HOPFIELD J. Simple “neural” optimization networks:an A/D converter, signal decision circuit, and a linear programming circuit[J]. IEEE Trans Circuits Syst,1986,33(5):533-541. [3] HOPFIELD J, TANK D. Neural computation of decision optimization problems[J]. Biol Cybernet,1985,52:141-154. [4] TALAVAN P, YANEZ J. Parameter setting of the Hopfield networks applied to TSP[J]. Neural Networks,2002,15(3):363-373. [5] FORTI M, TESI A. New conditions for global stability of neural networks with application to linear and quadratic programming problems[J]. IEEE Trans Circuits Syst I,1995,42(7):354-365. [6] LEE D. Pattern sequence recognition using a time-varying Hopfield networks[J]. IEEE Trans Neural Netw,2002,13(2):330-342. [7] FARREL J, MICHEL A. A synthesis procedure for Hopfield’s continuous-time associative memory[J]. IEEE Trans Circuits Syst,1990,37(7):877-884. [8] CHENG C, LIN K, SHIH C. Multistability in recurrent neural networks[J]. SIAM J Appl Math,2006,66(4):1301-1320. [9] HAYKIN S. Neural Networks:A Comprehensive Foundation[M]. New Jersey:Prentice-Hall,1998. [10] MICHEL A, FARRELL J, POROOD W. Qualitative analysis of neural networks[J]. IEEE Trans Circuits and Systems,1989,36(2):229-243. [11] WU J. Introduction to Neural Dynamics and Signal Transmission Delay[M]. Berlin:Walter de Gruyter,2001. [12] MARCUS C, WESTERVELT R. Stability of analog neural networks with delay[J]. Phys Rev,1989,A39:347-359. [13] GOPALSAMY K, HE X. Stability in asymmetric Hopfield nets with transmission delays[J]. Physica D,1994,76:344-358. [14] DRIESSCHE P, ZOU X. Global attractivity in delayed Hopfield neural network models[J]. SIAM J Appl Math,1998,58(6):1878-1890. [15] ZHANG J, JIN X. Global stability analysis in delayed Hopfield neural networks models[J]. Neural Networks,2000,13:745-753. [16] MARCO M, FORTI M, GRANZZINI M, et al. Limit set dichotomy and multistability for a class of cooperative neural networks with delays[J]. IEEE Trans Neural Netw Learn Syst,2012,23(9):1473-1485. [17] CHENG C, LIN K, SHIH C, et al. Multistability for delayed neural networks via sequential contracting[J]. IEEE Trans Neural Netw Learn Syst,2015,26(12):3109-3122. [18] EDUARDO L, ALFONSO R. Attractivity, multistability,and bifurcation in delayed Hopfield’s model with non-monotonic feedback[J]. J Diff Eqns,2013,255:4244-4266. [19] CHEN T. New theorems on global convergece of some dynamical systems[J]. Neural networks,2001,14:251-255. [20] Zhang W. A weak condition of globally asymptotic stability for neural networks[J]. Applied Mathematics Letters,2006,19:1210-1215. [21] CHEN T, AMARI S. Stability of asymmetric Hopfield networks[J]. IEEE Trans Neural Networks,2001,12(1):159-163. [22] ROUCHE N, HABETS P, LALOR M. Stability theory by Lyapunov’s Direct Method[M]. New York:Springer-Verlag,1977.1 预备知识
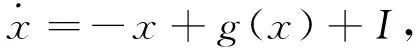
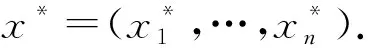

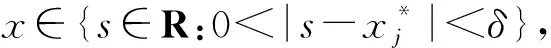
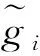
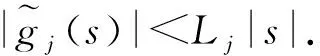

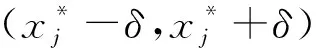
2 主要结论及证明