关于Janko群的新刻画
2018-06-04何立官陈贵云
何立官, 陈贵云
(1. 重庆师范大学 数学科学学院, 重庆 401331; 2. 西南大学 数学与统计学院, 重庆 400715)
1 引言及符号说明
有限群的数量刻画是群论领域的重要课题,一直以来,人们总是期望能用最少的数量条件去刻画群的最多性质.而“群的阶”和“群中元素的阶”是群的2个最基本的数量条件,且群的许多性质可以通过群的阶完整的反映出来,比如“奇数阶群可解定理”“paqb定理”等.那么类似的,可否借助于群中元素的阶来刻画群的性质呢?在20世纪80年代,Field奖获得者Thompson提出“同阶型群具有相同的可解性”这一有趣的猜想(该猜想由施武杰教授于1987年在澳大利亚国际会议上公开).
猜想1.1(J.G.Thompson猜想) 设G,M都是有限群,Sn(G)表示G群中n阶元组成的集合.如果|Sn(G)|=|Sn(M)|,n=1,2,3,…,那么G与M有相同的可解性,即G可解当且仅当M可解.
在同一时期,施武杰提出“用群阶和元素阶之集刻画有限单群”的猜想(文献[1]中的问题12.39).
猜想1.2(施武杰猜想) 设G是有限群,M是有限单群,则G≅M当且仅当|G|=|M|且πe(G)=πe(M),其中πe(G)表示群G中元素阶的集合.
猜想1.2于2009年被完全证明[2-9],但如何弱化该猜想的条件就成为大家关注的热点问题.文献[10-16]仅用高阶元的阶和群的阶刻画了系列单群,局部弱化了猜想1.2的条件.而猜想1.1至今都没有得到完整的解决,但人们从最高阶元的个数出发,证明了该猜想在一些特殊条件下是成立的[17-21].文献[10-21]说明最高阶元在刻画群的性质结构方面有着特殊的地位.受以上工作的启发,本文试图去掉“同阶型群”“群阶相等”“元素阶之集相同”这些重要的数量条件,只用与最高阶元有关的几个数量来刻画有限群特别是有限单群.为叙述方便,先对本文中出现的一些符号加以说明.
设G是有限群,G后括号中的数字表示G的阶.k是一个正整数,π(k)表示k的相异素因子的集合,特别地,π(G)=π(|G|),且记π(G)中的最大素数为lp(G).πe(G)表示群G中元素阶的集合,o1(G)表示G中最高阶元素的阶,n1(G)表示G中最高阶元素的个数.设G一共有r个o1(G)阶元,其中心化子的阶两两不同,并依次设这些中心化子的阶为ci(G)(i=1,2,…,r).令
ONC1(G)=
{o1(G);n1(G);c1(G),c2(G),…,cr(G)},
称ONC1(G)为G的第一ONC-度量.用Γ(G)表示G的素图,t(G)表示G的素图连通分支数,πi(i=1,2,…)表示Γ(G)的第i个连通分支所含顶点之集.如果2||G|,则总设2∈π1(见文献[22]).设m、n是两个整数,mk||n表示mk|n但mk+1⫮n.其余符号及术语是标准的.
本文用群的第一ONC-度量ONC1(G)刻画了Janko群J1、J3、J4,用ONC1(G)和lp(G)刻画了Janko群J2.
注1对Janko群来说,ONC1(G)只含3个数量,这说明J1、J3、J4只需要3个数量就可以完整刻画,所有Janko群最多需要4个数量就能完整刻画.而本文最大特点在于避开了“群阶相等”“群的元素阶之集相同”等重要的数量条件.
2 主要引理
引理2.1由文献[23]知,如果G为Janko群,那么|G|、ONC1(G)如表1给出.

表1 Janko 群的阶和第一ONC-度量
引理2.2[22]设G的素图分支大于1,则G的结构是如下之一:
1)G是Frobenius群或者2-Frobenius群;
2)G有一正规列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1.H为幂零群,而且|G/K|||Out(K/H)|.
引理2.3[24]设G是偶阶Frobenius群,K是Frobenius核,H是Frobenius补,则t(G)=2且T(G)={π(H),π(K)}.
引理2.4[24]设G是偶阶2-Frobenius群,则t(G)=2,且G有正规列1◁H◁K◁G,使得
π(K/H)=π2,π(H)∪π(G/K)=π1,
G/K和K/H均为循环群且满足|G/K|||Aut(K/H)|.特别地|G/K|<|K/H|,G可解.
引理2.5[25]设π′-群H作用在π-群G上,且G和H中至少有一个可解,则对任意素数p||G|,G中存在H-不变的Sylowp-子群,并且G的任意2个H-不变Sylowp-子群在CG(H)下共轭.
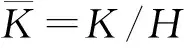
3 主要定理及证明
定理3.1设G为有限群,M为Janko群:J1,J3,J4,则G≅M的充分必要条件是ONC1(G)=ONC1(M).
证明必要性显然,下证充分性.
情形 1 设M=J1.由引理2.1知ONC1(G)=ONC1(J1)={19;23·3·5·7·11;19}.
可以看出G的19阶元都是自中心化的,所以G中任何19阶元a所在的共轭类长度都是
设G中19阶元一共分为t个共轭类,则
t·|G|/19=23·3·5·7·11,
从而|G||23·3·5·7·11·19.由
n1(G)=23·3·5·7·11
知|G|≥23·3·5·7·11,因此必有7∈π(G)或11∈π(G).又因为o1(G)=19,所以19∈π(G).故{7,19}⊆π(G)或{11,19}⊆π(G).
由o1(G)=19知19是Γ(G)的孤立点,从而t(G)≥2.由引理2.2知G或者是Frobenius群,或者是2-Frobenius群,或者G有一正规子群列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1,H为幂零群,而且
|G/K|||Out(K/H)|.
下证G既不是Frobenius群也不是2-Frobenius群.
设G是Frobenius群.由引理2.3知t(G)=2且Γ(G)={π(H),π(K)},其中K是Frobenius核,H是Frobenius补.所以K要么是G的Sylow19-子群,要么是G的19′-Hall子群.设S为K的一个Sylow子群,因为K幂零,所以有|H||(|S|-1).于是可以选择一个适当的Sylow-子群S,使得
|H||(|S|-1),
从而得出矛盾.显然K不是Sylow19-子群.故设K是19′-Hall子群.考虑K的Sylow7-子群或Sylow11-子群,有19|(7-1)或19|(11-1),矛盾.因此G不是Frobenius群.
如果G是2-Frobenius群,则由引理2.4知t(G)=2,且G有正规列1◁H◁K◁G,使得
π(K/H)=π2,π(H)∪π(G/K)=π1,
|G/K|||Aut(K/H)|.
因为19是Γ(G)的孤立点,所以π2={19},于是
π(H)∪π(G/K)⊆{2,3,5,7,11}
且|K/H|=19.又因为|G/K|||Aut(K/H)|,所以p⫮|G/K|,于是p||H|,其中p=7或11.用G中19阶元g共轭作用在H上,由引理2.5知存在H的Sylowp-子群L在该作用下不变.显然有
19⫮ |Aut(L)|,
即g平凡作用在L上,故G中有阶大于19的元,矛盾.因此G不是2-Frobenius群.
于是G有一正规列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1,H为幂零群,而且|G/K|||Out(K/H)|.因为19是Γ(G)的孤立点,所以
π(H)∪π(G/K)⊆{2,3,5,7,11},
而19∈π(K/H).由文献[23]知
K/H≅L2(19)(22·32·5·19),
或K/H≅J1(23·3·5·7·11·19).
设K/H≅L2(19).因为|Out(L2(19))|=2,所以|G/K|=1或2,因此p||H|,其中p=7或11.设L为H的Sylowp-子群,则|L|=p.因为H幂零,所以L◁G.用G中19阶元作用在L上,该作用平凡,从而产生阶大于19的元,矛盾.
设K/H≅J1.如果|G|=23·3·5·7·11·19,那么G≅J1.于是设|G|=23·32·5·7·11·19.因为|Out(J1|=1,所以|G/K|=1,从而|H|=3.用G中19阶元作用在H上,有57∈πe(G),矛盾.于是G≅J1.
情形 2 设M=J3.由引理2.1知ONC1(G)=ONC1(J3)={19;28·35·5·17;19}.
类似情形1的证明可知|G||28·35·5·17·19,{5,19}⊆π(G)或{17,19}⊆π(G),且33||G|.同时G有一正规列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1,H为幂零群,而且|G/K|||Out(K/H)|.因为19是Γ(G)的孤立点,所以π(H)∪π(G/K)⊆{2,3,5,17},19∈π(K/H).于是由文献[23]和文献[12]中的表3知
K/H≅L2(19)(22·32·5·19),
或K/H≅J3(27·35·5·17·19).
设K/H≅L2(19).因为|Out(L2(19))|=2,所以|G/K|=1或2,因此3||H|.设L为H的Sylow3-子群,则L◁G且|L||33.考虑Ω1(Z(L)),显然Ω1(Z(L))为初等交换3-群且Ω1(Z(L))◁G.由于|Ω1(Z(L))||33,故19⫮|Aut(Ω1(Z(L)))|.用G中19阶元作用在Ω1(Z(L))上,该作用平凡,从而57∈πe(G),矛盾.
设K/H≅J3.如果|G|=27·35·5·17·19,那么G≅J3.于是设|G|=28·35·5·17·19.因为|Out(J3|=2,所以|G/K|=1或2.如果|G/K|=1,则|H|=2.用G中19阶元作用在H上,有38∈πe(G),矛盾.从而|G/K|=2,此时K/H=K≅J3,故G=J3×Z2或G=J3Z2.如果G=J3×Z2,则38∈πe(G),矛盾.如果G=J3Z2,则o1(G)=34,矛盾.于是G≅J3.
情形 3 设M=J4.由引理2.1知
ONC1(G)=ONC1(J4)=
{66;221·33·5·7·112·23·29·31·37·43;66}.
类似情形1的讨论有|G||222·33·5·7·113·23·29·31·37·43,{2,3,11}⊆π(G).断言43||G|.否则|G|=222·33·5·7·113·23·29·31·37.易证G有一正规列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1,H为幂零群,而且|G/K|||Out(K/H)|.因为37是Γ(G)的孤立点,所以
π(H)∪π(G/K)⊆{2,3,5,7,11,23,29,31},
37∈π(K/H).由文献[23]和[12]中的表3知
K/H≅U3(11)(25·32·5·113·37).
此时29||H|.用37阶元作用在H的Sylow29-子群上,该作用产生阶大于66的元,矛盾.于是43||G|.同理可得G有一正规列1◁H◁K◁G,使得H和G/K是π1-群,K/H是非交换单群,其中2∈π1,H为幂零群,而且|G/K|||Out(K/H)|.因为37,43都是Γ(G)的孤立点,所以37,43∈π(K/H).再由文献[23]和文献[12]中的表3知只有
K/H≅
J4(221·33·5·7·113·23·29·31·37·43).
如果
|G|=221·33·5·7·113·23·29·31·37·43,
那么G≅J4.于是设
|G|=222·33·5·7·113·23·29·31·37·43.
因为|Out(J4)|=1,所以|G/K||1,因此|H|=2.用G中43阶元作用在H上,有86∈πe(G),矛盾.于是G≅J4.
定理证毕.
定理3.2设G为有限群,则G≅J2的充分必要条件是ONC1(G)=ONC1(J2)且lp(G)=lp(J2).
证明必要性显然,下证充分性.
由引理2.1知
ONC1(G)=ONC1(J2)={15;28·32·5·7;15},
lp(G)=lp(J2)=7.此时有
|G||28·33·52·7,π(G)={2,3,5,7}.

A7(23·32·5·7),A8(26·32·5·7),
L3(4)(26·32·5·7),J2(27·33·52·7).


Out(L3(4))=2×S3,
所以|Aut(L3(4))|=28·33·5·7.如果52||G|,那么5||C|.用G的7阶元作用在C的Sylow5-子群上,则有35∈πe(G),矛盾.于是5|||G|,此时|G|=28·33·5·7.如果3||C|,那么用G的7阶元作用在C的Sylow3-子群上,则有21∈πe(G),矛盾.因此3⫮|C|.设2||C|,比较阶知|C||4.如果|C|=2,那么用G的15阶元作用在C上,则有30∈πe(G),矛盾.如果|C|=4,那么由文献[23]知G/C≅L3(4)Z3,此时有21∈πe(G),矛盾.故C=1,从而G≅Aut(L3(4),但o1(Aut(L3(4)))=21,矛盾.

|G|=28·33·52·7.
如果|H|=2,用15阶元作用在H上,则有30∈πe(G),矛盾.因此设H=1.由|Out(J2)|=2知G≅J2×Z2或G≅J2Z2.如果G≅J2×Z2,则30∈πe(G),矛盾.如果G≅J2Z2,则G≅Aut(J2),此时o1(G)=24,矛盾.从而G≅J2.
定理证毕.
最后,提出1个问题:是否存在反例说明定理3.2中条件lp(G)=7是必要的.
[1] MAZUROV V D, KHUKHRO E I. Unsolved Problems in Group Theory[M]. Novosibirsk:Institute of Mathematics,Russian Academy of Sciences,2010:60.
[2] SHI W J. A new characterization of the sporadic simple groups[C]//Group Theory Porc Singapore Group Theory Conf,1987.Berlin:Walter de Gruyter,1989:531-540.
[3] SHI W J, BI J X. A characterization of the alternating groups[J]. Southeast Asian Bulletin of Mathematics,1992,16(1):81-90.
[4] SHI W J, BI J X. A characterization of Suzuki-Reegroups[J]. Science in China,1991,A34(1):14-19.
[5] SHI W J, BI J X. A characteristic property for each finite projective special linear group[J]. Lecture Notes in Math,1990,1456:171-180.
[6] SHI W J. Pure quantitative characterization of finite simple groups[J]. Progress in Nature Science,1994,4(3):316-326.
[7] CAO H P, SHI W J. Pure quantitative characterization of finite projective special unitary groups[J]. Science in China,2002,A45(6):761-772.
[8] XU M C, SHI W J. Pure quantitative characterization of finite simple groups2Dn(q) andDl(q)(lodd)[J]. Algebra Colloquium,2003,10(3):427-443.
[9] VASIL’EV A V, GRECHKOSEEVA M A, MAZUROV V D. Characterization of the finite simple Groups by spectrum and order[J]. Algebra and Logic,2009,48(6): 385-409.
[10] HE L G, CHEN G Y. A new characterization of simpleK3-groups[J]. Communications in Algebra,2012,40(10):3903-3911.
[11] HE L G, CHEN G Y. A new characterization ofL2(q) whereq=pn<125[J]. Italian J Pure and Applied Mathematics,2011,28:127-136.
[12] HE L G, CHEN G Y, XU H J. A new characterization of Sporadic Simple Groups[J]. Italian J Pure and Applied Mathematics,2013,30: 373-392.
[13] HE L G, CHEN G Y. A new characterization of simpleK4-groups with TypeL2(p)[J]. 数学进展,2014,43(5):667-670.
[14] 何立官,徐海静. 关于单K3-群的自同构群的刻画[J]. 数学进展,2015,44(3):363-368.
[15] HE L G, CHEN G Y. A new characterization of simpleK4- groups[J]. J Mathematical Research with Applications,2015,35(4):400-406.
[16] 高彦伟,曹洪平,陈贵云. 散在单群的新刻画[J]. 数学年刊,2016,A37(1):109-144.
[17] 杨成. 最高阶元素个数不同的有限群[J]. 数学年刊,1993,14(5):561-576.
[18] 姜友谊. 最高阶元素个数为2p2的有限群是可解群[J]. 数学年刊,2000,21(1):61-64.
[19] 杜祥林,姜友谊. 最高阶元素个数为4p的有限群[J]. 数学年刊,2004,29(3):198-200.
[20] HE L G, CHEN G Y. Solvability of finite groups with 10pelements of maximal order[J]. Appl Math Computer,2006,21(1):431-436.
[21] 何立官,陈贵云. 最高阶元素个数为10pm的有限群可解[J]. 西南大学学报(自然科学版),2007,29(6):1-4.
[22] WILLIAMS J S. Prime graph components of finite group[J]. J Algbra,1981,69(2):487-513.
[23] CONWAY J H, CURTIS R T, NORTON S P, et al. ATLAS of Finite Groups[M]. New York:Oxford University Press,1985.
[24] 陈贵云. 关于Frobenius群和2-Frobenius群[J]. 西南师范大学学报(自然科学版),1995,20(5):485-487.
[25] 徐明曜. 有限群初步[M]. 北京:科学出版社,2014:267-267.
