随机变分不等式的随机投影梯度算法
2018-06-04夏福全
杨 灿, 夏福全
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
1 引言及预备知识
本文主要研究如下的随机变分不等式问题:求x∈C使得
〈E[f(x,ξ(θ))],y-x〉≥0, ∀y∈C,
(1)
其中,C是Rn中的非空闭凸子集,f(x,ξ):Rn×Rk→Rn是一个连续映射,ξ:Ω→Rk是定义在某概率空间(Ω,Λ,P)上的随机变量,E[f(x,ξ(θ))]表示f(x,ξ(θ))相对于分布ξ的期望值.
众所周知,变分不等式问题在交通、经济平衡、博弈论和网络问题等方面都有着重要应用[1-5].在实际生活中,虽然许多问题只涉及到确定的数据,但也有很多问题的数据包含随机变量,比如几个公司提供可替代商品的库存和服务的价格竞争[6-7]、一些随机动态博弈[8-9].很多包含随机变量的问题都可以归结为带有随机变量的变分不等式模型,即随机变分不等式问题.随机变分不等式问题是一般变分不等式问题的一个推广[10-12],但关于随机变分不等式的理论与算法都非常有限.由于随机变分不等式有着广泛的应用,因而,随机变分不等式问题引起了越来越多的专家学者的关注和研究.
令F(x)=E[f(x,ξ(θ))],则(1)式变为下列的一般变分不等式问题:求x∈C满足
〈F(x),y-x〉≥0, ∀y∈C.
(2)
对于经典的变分不等式问题(2),已经有非常多的有效的方法可以求解.因此,当E[f(x,ξ(θ))]容易计算时,随机变分不等式问题容易求解.但在实际应用中,E[f(x,ξ(θ))]的计算一般比较困难,比如虽然函数f(x,ξ(θ))已知,但是ξ的分布未知并且ξ的信息只能从过去样本的数据中获得;或者E[f(x,ξ(θ))]必须通过模拟近似估算而不能直接获得.在这些情况下,已有求解一般变分不等式的数值方法等都不能直接用于求解随机变分不等式问题.
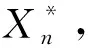
最近,Malitsky[26]提出了求解变分不等式问题(2)的一种新的数值方法——投影反射梯度算法,具体迭代过程是:
xn+1=PC(xn-λ(F(yn)),
yn=2xn-xn-1,
其中,PC表示在集合C上的投影,λ>0是常数.为了证明该算法所产生的迭代序列的收敛性,假设F是伪单调以及Lipschitz连续的.该算法的优点在于:在迭代的每一步,只需要向可行集进行一次投影,迭代中也只需对函数F赋值一次.数值结果表明该算法快速且有效.
本文主要的工作是结合Malitsky[26]的投影反射梯度算法和随机逼近方法,给出了随机变分不等式(1)的随机投影梯度方法.该方法结合了Malitsky[26]算法和随机逼近方法的优点,因而算法简单快速.在一定条件下,证明了该算法所产生的迭代序列的全局收敛性.
定义1.1设C⊂Rn为非空闭凸集,对任意x∈Rn,定义
PC(x):=argmin{‖x-y‖:y∈C},
称PC(x)是x在C上的投影.
定义1.2称映射F:Rn→Rn是:
1) 单调的,若对于任意的x,y∈Rn,有
〈F(x)-F(y),x-y〉≥0;
2) 是伪单调的,若对于任意的x,y∈Rn,有
〈F(y),x-y〉≥0⟹〈F(x),x-y〉≥0;
3) 是伪单调-加的,若F是伪单调的,且对于任意的x,y∈Rn,有
〈F(x),x-y〉=0,〈F(y),x-y〉≥
0⟹F(x)=F(y);
4)Lipschitz连续的,若存在常数L>0,对于任意的x,y∈Rn,有
‖F(x)-F(y)‖≤L‖x-y‖.
引理1.1[27]设C是Rn中的非空闭凸集,对任意x∈Rn,则:
1) 〈PC(x)-x,y-PC(x)〉≥0,∀y∈C;
2) ‖PC(x)-y‖2≤‖x-y‖2-‖x-PC(x)‖2,∀y∈C.
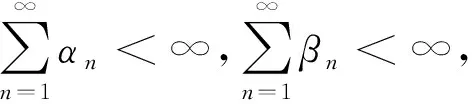
E[Vn+1|Fn]≤(1+αn)Vn-γn+βn,
(3)
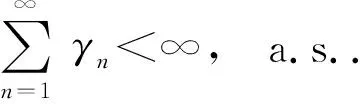
2 算法及其收敛性
总假设F(x)=E[f(x,ξ(θ))]且F是Lipschitz连续映射,其Lipschitz连续系数为L>0.对每个n≥0,令ωn=f(xn,ξn)-F(xn).对给定的常数λ>0,设
r(x,y):=‖y-PC(x-λF(y))‖+‖x-y‖.
首先介绍随机变分不等式问题(2)解的迭代算法.
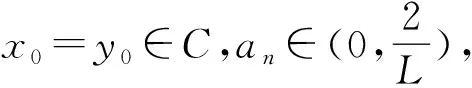
2) 对当前的迭代点xn和yn,令
xn+1=PC(xn-an(F(yn)+ωn)).
(4)
若r(xn,yn)=0,则算法停止.否则,计算
yn+1=2xn+1-xn;
(5)
3) 令n=n+1,回到2).
显然,ωn=f(xn,ξn)-F(xn)是随机误差.易知,在迭代的第n步,用ξ的一个样本ξn计算f(xn,ξn),并把它当作F(xn)的一个近似.因此,当近似F(xn)时,不需要知道变量ξ的概率分布.这非常有利于算法的实现.
对任意n≥1,首先定义与算法2.1相关的σ-域为
Fn=(w0,w1,…,wn-1,y0,y1,…yn-1,x0,x1,…xn}.
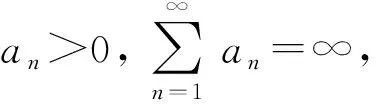
(b)E[ωn|Fn]=0;
易知,假设2.1中条件(a)是随机逼近中选择步长的一个准则,参见文献[29].假设条件(b)和(c)表示随机误差ωn是无偏的且是受控的方差标度.这些假设是随机逼近方法相关文献中的常用准则.
引理2.1若变分不等式问题(1)的解集S非空,z∈S且F:Rn→Rn为Lipschitz连续映射,则由算法2.1所生成的序列{xn}和{yn}满足
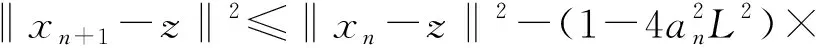
(6)
证明根据xn+1=PC(xn-an(F(yn)+wn))以及引理2.1的2)有
‖xn+1-z‖2≤‖xn-an(F(yn)+wn)-z‖2-
‖xn-an(F(yn)+wn)-xn+1‖2=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn)+wn,xn-z〉+
2an〈F(yn)+wn,xn-xn+1〉=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn)+wn,xn+1-z〉=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn),xn+1-z〉-2an〈wn,xn+1-z〉.
(7)
易知
-2an〈F(yn),xn+1-z〉=
-2an〈F(yn)-F(yn-1),xn+1-yn〉-
2an〈F(yn-1),xn+1-yn〉-
2an〈F(yn),yn-z〉.
(8)
由于{xn}⊂C,根据
xn=PC(xn-1-an(F(yn-1)+wn-1))
以及引理1.1的1)有
〈xn-xn-1+an(F(yn-1)+wn-1,xn-xn+1〉≤0,
〈xn-xn-1+an(F(yn-1)+wn-1,xn-xn-1〉≤0.
上述两式相加,注意到yn=2xn-xn-1,有
〈xn-xn-1+an(F(yn-1)+wn-1),yn-xn+1〉≤0.
从而,根据xn-xn-1=yn-xn及上式可推知
2an〈F(yn-1),yn-xn+1〉≤
2〈xn-xn-1,xn+1-yn〉+2an〈wn-1,xn+1-yn〉=
2〈yn-xn,xn+1-yn〉+2an〈wn-1,xn+1-yn〉=
‖xn+1-xn‖2-‖xn-yn‖2-
‖xn+1-yn‖2+2an〈wn-1,xn+1-yn〉.
(9)
另一方面,由于F是Lipschitz连续映射,则
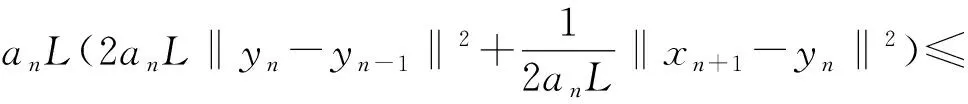
(10)
此外,根据Cauchy-Schwarz不等式及均值不等式,易知
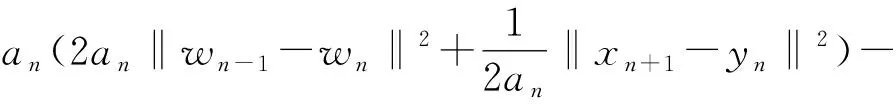
(11)
将(8)~(10)式代入(7)式得到
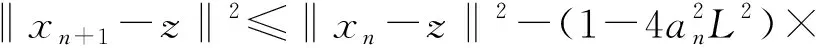
(12)
引理得证.
选取常数λ>0满足下列不等式
事实上,由于an→0(n→∞),当n充分大时,可以选取充分大λ>0满足(13)式.
引理2.2若变分不等式问题(1)的解集S非空,z∈S且F:Rn→Rn为Lipschitz连续映射,则由算法2.1所生成的序列{xn}和{yn}满足
(14)
其中λ>0满足(13)式.
证明设z∈S,选取λ>0满足(13)式,根据F的Lipschitz连续性以及Cauchy-Schwarz不等式有
2an〈F(yn),yn-z〉=
〈F(yn)-F(xn),yn-z〉+2an〈F(xn),yn-z〉≥
-2anL‖yn-xn‖‖yn-z‖+2an〈F(xn),yn-z〉≥
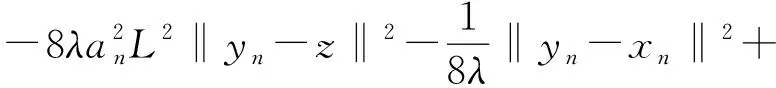
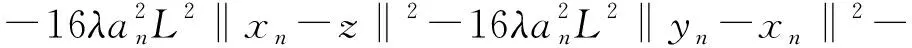
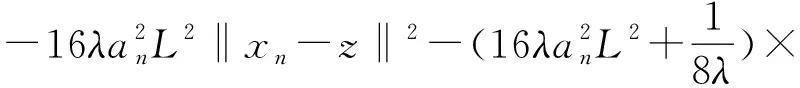
(15)
另一方面,根据F的Lipschitz连续性以及Cauchy-Schwarz不等式有
2an〈F(xn),yn-z〉=
2an〈F(xn),yn-xn〉+2an〈F(xn),xn-z〉=
2an〈F(xn)-F(yn),yn-xn〉+
2an〈F(yn),yn-xn〉+2an〈F(xn),xn-z〉≥
-2anL‖yn-xn‖-2an‖F(yn)‖×
‖yn-xn‖+2an〈F(xn),xn-z〉≥
-2anL‖yn-xn‖-2an‖F(yn)-F(z)‖×
‖yn-xn‖-2an‖F(z)‖‖yn-xn‖+
2an〈F(xn),xn-z〉≥-2anL‖yn-xn‖-
2anL‖yn-z‖‖yn-xn‖-
2an‖F(z)‖‖yn-xn‖+2an〈F(xn),xn-z〉≥
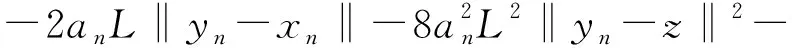
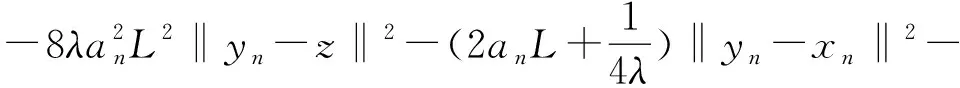
将(16)式代入(15)式可得(14)式,结论成立.
定理2.1假设变分不等式问题(1)的解集S非空,F:Rn→Rn为伪单调-加Lipschitz连续映射,则由算法2.1所生成的序列{xn}几乎处处收敛于问题(1)的解.
证明对任意z∈S,λ>0满足(13)式,根据引理2.1和引理2.2有
‖xn+1-z‖2≤
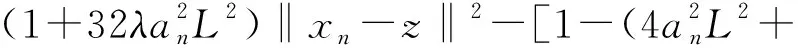
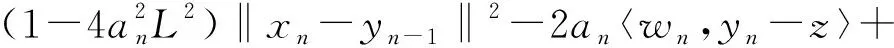
根据(17)式及假设条件2.1可得
E[‖xn+1-z‖2|Fn]≤
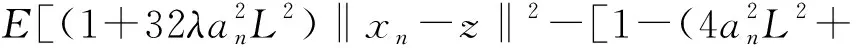
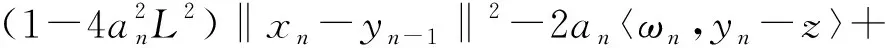
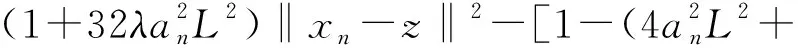
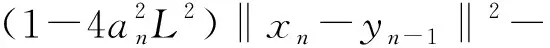
(18)
令
由假设条件2.1及(13)式可知,对充分大的n有,ξn>0,ηn>0,从而(18)式变为
E[‖xn+1-z‖2|Fn]≤
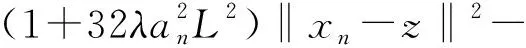
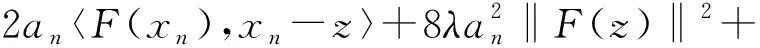
(19)
再设
γn=ξn‖xn-yn‖2+ηn‖xn-yn-1‖2+
2an〈F(xn),xn-z〉,
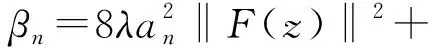
(20)
注意到z∈S是变分不等式(1)的解,xn∈C,故
〈F(xn),xn-z〉≥0.
(21)
另外,根据假设条件2.1及(13)式可知
(22)
从而根据(20)~(22)式可知
(23)
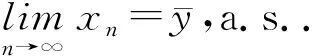
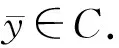
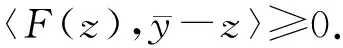
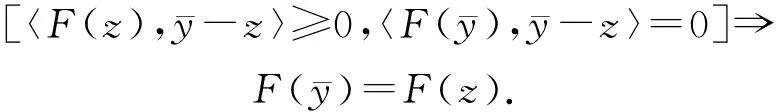
此外,对任意的y∈C,由于z∈S,有〈F(z),y-z〉≥0.因此,对任意的y∈C有
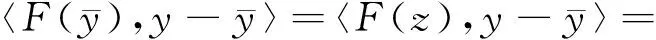
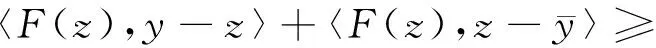
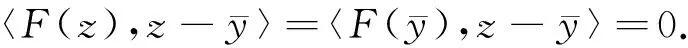
由于对任意x∈C,F(x)=E[f(x,ξ(θ))],故
〈E[f(x,ξ(θ))],y-x〉≥0, ∀y∈C,
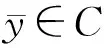
[1]BREZISH.Opérateursmaximauxmonotones:etsemi-groupesdecontractionsdanslesespacesdeHilbert[J].JAcousticalSocietyAmerica,1989,125(4):2680.
[2]GIANNESSIF,MaugeriA.VariationalInequalityandNetworkEquilibriumProblems[M].NewYork:PlenumPress,1995:315-320.
[3]VERMARU.Generalconvergenceanalysisfortwo-stepprojectionmethodsandapplicationtovariationalproblems[J].ApplMathLett,2005,18(11):1286-1292.
[4]FACCHINEIF,PANGJS.Finite-dimensionalVariationalInequalitiesandComplementaryProblemsVolumeI/II[M].NewYork:Springer-Verlag,2003.
[5]LUOZQ,PANGJS,RALPHD.MathematicalProgramswithEquilibriumConstraints[M].Cambridge:CambridgeUniversityPress,1996.
[6]CHENFY,YANH,YAOL.Anewsvendorpricinggame[J].IEEETransactionsonSystemsManandCyberneticsPartASystemsandHumans,2004,34(4):450-456.
[7]CMAHAIANS,VANRYZING.Inventorycompetitionunderdynamicconsumerchoice[J].OperationsResearch,2001,49(5):464-657.
[8]BASART,OLSDERG.DynamicNoncooperativeGameTheory[M].Philadeiphia:SIAM,1999.
[9]FILARJ,VRIEZEK.CompetitiveMarkovDecisionProcesses[M].Berlin:Springer-Verlag,1996.
[10]GURKANG, ÖZGEAY,ROBINSONSM,etal.Samplepathsolutionofstochasticvariationalinequalities,withapplicationstooptionpricing[C].Proceedingsofthe28thconferenceonWintersimulation-WSC96,1996.DOI:10.1145/256562.256646.
[11]GURKANG,OZGEAY,ROBINSONSM.Sample-pathsolutionofstochasticvariationalinequalities[J].MathematicalProgramming,1999,84(2):313-333.
[12]ROBINSONSM.Analysisofsample-pathoptimization[J].MathematicsofOperationsResearch,1996,21(3):513-528.
[13]SHAPIROA,DENTCHEVAD,RUSZCZYNSKIA.LecturesonStochasticProgramming:ModelingandTheory[M].Philadeiphia:SIAM,2009.
[14]XUH.Sampleaverageapproximationmethodsforaclassofstochasticvariationalinequalityproblems[J].AsiaPacificOperationalResearch,2011,27(1):103-119.
[15]ROBBINSH,MONROS.Astochasticapproximationmethod[J].AnnMathematicalStatistics,1951,22(3):400-407.
[16]ROBINSONSM,MONROS.Onastochasticapproximationmethod[J].AnnMathematicalStatistics,1954,25(3):463-483.
[17]JIANGHY,XUHF.Stochasticapproximationapproachestothestochasticvariationalinequalityproblem[J].IEEETransactionsonAutomaticControl,2008,53(6):1462-1475.
[18]KOSHALJ,NEDICA,SHANBHAGUV.Regularizediterativestochasticapproximationmethodsforstochasticvariationalinequalityproblems[J].IEEETransactionsonAutomaticControl,2013,58(3):594-609.
[19]NEMIROVSKIA,JUDITSKYA,LANG,etal.Robuststochasticapproximationapproachtostochasticprogramming[J].SIAMJOptim,2009,19(4):1574-1609.
[20]JUDITSKYA,NEMIROVSKIA,TAUVELC.Solvingvariationalinequalitieswithstochasticmirror-proxalgorithm[J].StochasticSystems,2011,1(1):17-58.
[21]BERTSEKASDP,TSITSIKLISJM.Neuro-dynamicprogramming[J].AthenaScientific,1996,27:1687-1692.
[22]ERMOLIEVY.StochasticQuasigradientMethods,NumericalTechniquesforStochasticOptimization[M].NewYork:Springer-Verlag,1988.
[23]KUSHNERHJ,YING.StochasticApproximationandRecursiveAlgorithmsandApplications[M].NewYork:Springer-Verlag,2003.
[24]ORMANA.Optimizationofstochasticmodels,theinterfacebetweensimulationandoptimization[J].OperationalResearchSociety,1998,49(6):675-675.
[25]FREYJ.Introductiontostochasticsearchandoptimization:estimation,simulation,andcontrol[J].Wiley-Interscience,2004,46(3):368-369.
[26]MALITSKYY.Projectedreflectedgradientmethodsformonotonevariationalinequalities[J].SIAMJOptim,2015,25(1):502-520.
[27]BAIOCCHIC,CAPELOA.VariationalandQuasivariationalInequalities[M].NewYork:JohnWiley,1984.
[28]ROBBINSH,SIEGMUNDD.Aconvergencetheoremfornonnegativealmostsupermartingalesandsomeapplications[C]//OptimizingMethodsinStatistics.RustagiJS,ed.NewYork:Academic,1971:233-257.
[29]PFLUGGC.Optimizationofstochasticmodels[C]//TheInterfaceBetweenSimulationandOptimization.NewYork:KluwerAcademic,1996.
